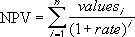NPV (funkcija NPV)

Sintaksa

NPV(stopa,vrednost1,vrednost2,...)

Stopa     je stopa popusta tokom perioda.

Vrednost1, vrednost2,...     predstavlja 1 do 29 argumenata koji predstavljaju isplate i prihode. Vrednost1, vrednost2,... mora biti jednako razmaknuto u vremenu i da se pojavljuje na kraju svakog perioda. NPV koristi redosled vrednosti1, vrednost2,... da biste tumačili redosled priliva sredstava. Uverite se da su vrednosti odliva i priliva sredstava navedene pravilnim redom. Broje se argumenti koji su brojevi, prazni, logičke vrednosti ili tekstualne predstave brojeva; argumenti koji su vrednosti grešaka ili tekst koji se ne može prevesti u brojeve se zanemaruju.

Primedbe

• NPV investicija započinje jedan period pre datuma vrednost1 za priliv sredstava i završava se poslednjim prilivom sredstava na listi. Izračunavanje NPV vrednosti se zasniva na budućem prilivu sredstava. Ako do prvog priliva sredstava dođe na početku prvog perioda, prva vrednost mora da se doda na rezultat NPV funkcije a ne uključena u vrednosti argumenata. Za više informacija pogledajte sledeće primere.

• Ako je n broj priliva sredstava na listi vrednosti, formula za NPV glasi:

  

• Funkcija NPV je slična funkciji PV (sadašnja vrednost). Osnovna razlika između funkcija PV i NPV jeste ta što PV omogućava da priliv sredstava počne i na početku i na kraju perioda. Za razliku od promenljivih vrednosti priliva sredstava u funkciji NPV, priliv sredstava u funkciji PV mora biti konstantan u toku celog investicionog perioda. Za više informacija o anuitetima i finansijskim funkcijama pogledajte funkciju PV.

Primer 1

U sledećem primeru:

• Stopa je godišnja diskontna stopa.

• Vrednost1 je početna investicija za godinu dana od danas.

• Vrednost2 je povraćaj iz prve godine.

• Vrednost3 je povraćaj iz druge godine.

• Vrednost4 je povraćaj u trećoj godini.

U primeru, kao jednu od vrednosti uključujete početnih 10.000 USD, zato što se uplata obavlja na kraju prvog perioda.

Primer 2

U sledećem primeru:

• Stopa je godišnja diskontna stopa. Ona može da predstavlja stopu inflacije ili kamatnu stopu konkurentne investicije.

• Vrednost1 je početna investicija za godinu dana od danas.

• Vrednost2 je povraćaj iz prve godine.

• Vrednost3 je povraćaj iz druge godine.

• Vrednost4 je povraćaj u trećoj godini.

• Vrednost5 je povraćaj u četvrtoj godini.

• Vrednost6 je povraćaj u petoj godini.

U primeru ne uključujete početnih 40.000 USD trošak kao jednu od vrednosti, zato što plaćanje počinje na početku prvog perioda.