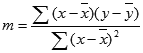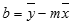บทความนี้จะอธิบายเกี่ยวกับไวยากรณ์ของสูตรและการใช้ฟังก์ชันLINESTใน Microsoft Excel ค้นหาลิงก์ไปยังข้อมูลเพิ่มเติมเกี่ยวกับแผนภูมิและการวิเคราะห์การถดถอย ได้ในส่วน ดูเพิ่มเติม
คำอธิบาย
ฟังก์ชัน LINEST จะคํานวณสถิติของเส้นโดยใช้วิธี "ค่าสี่เหลี่ยมน้อยที่สุด" เพื่อคํานวณเส้นตรงที่เหมาะสมกับข้อมูลของคุณที่สุด แล้วส่งกลับอาร์เรย์ที่อธิบายเส้นตรงนั้น คุณยังสามารถรวม LINEST กับฟังก์ชันอื่นๆ เพื่อคํานวณสถิติของโมเดลชนิดอื่นๆ ที่เป็นเชิงเส้นในพารามิเตอร์ที่ไม่รู้จัก รวมถึงพหุภูมิ ลอการิทมิก เอ็กซ์โพเนนเชียล และ Power Series เนื่องจากฟังก์ชันนี้ส่งกลับอาร์เรย์ของค่าต่างๆ ฟังก์ชันจึงต้องใส่ค่าเป็นสูตรอาร์เรย์ คําแนะนําตามตัวอย่างในบทความนี้
สมการของเส้นตรงคือ
y = mx + b
หรือ
y = m1x1 + m2x2 + ... + b
ถ้ามีช่วงของค่า x อยู่หลายช่วง โดยที่ค่า y ที่ขึ้นต่อกันคือฟังก์ชันของค่า x อิสระ ค่า m คือสัมประสิทธิ์ที่สอดคล้องกับค่า x แต่ละค่า และ b เป็นค่าคงที่ โปรดทราบว่า y, x และ m อาจเป็นเวกเตอร์ได้ อาร์เรย์ที่ฟังก์ชัน LINEST ส่งกลับคือ {mn,mn-1,...,m1,b} LINEST ยังสามารถส่งกลับค่าสถิติการถดถอยเพิ่มเติมได้
ไวยากรณ์
LINEST(known_y's, [known_x's], [const], [stats])
ไวยากรณ์ของฟังก์ชัน LINEST มีอาร์กิวเมนต์ดังนี้
ไวยากรณ์
-
known_yของ จำเป็น ชุดของค่า y ที่คุณทราบอยู่แล้วในความสัมพันธ์ y = mx + b
-
ถ้าช่วงของ known_y อยู่ในคอลัมน์เดียว แต่ละคอลัมน์ของ known_x's จะถูกแปลงเป็นตัวแปรแยกต่างหาก
-
ถ้าช่วงของ known_y อยู่ในแถวเดียว แต่ละแถวของ known_x จะถูกแปลงเป็นตัวแปรแยกต่างหาก
-
-
known_xของ ไม่จำเป็น ชุดของค่า x ที่คุณอาจทราบอยู่แล้วในความสัมพันธ์ y = mx + b
-
ช่วง ของknown_xสามารถ รวมชุดของตัวแปรอย่างน้อยหนึ่งชุดได้ ถ้ามีการใช้เพียงหนึ่งตัวแปร known_y'sและ known_x สามารถเป็นช่วงของรูปร่างใดก็ได้ ตราบใดที่รูปร่างมีขนาดเท่ากัน ถ้ามีการใช้มากกว่าหนึ่งตัวแปร known_yต้องเป็น เวกเตอร์ (นั่นคือ ช่วงที่มีความสูงหนึ่งแถวหรือความกว้างของหนึ่งคอลัมน์)
-
ถ้าไม่ได้ใส่ค่าอาร์เรย์ known_x's อาร์เรย์จะถูกกำหนดเป็นอาร์เรย์ {1,2,3,...} ที่มีขนาดเท่ากับอาร์เรย์ known_y's
-
-
const ไม่จำเป็น ค่าตรรกะที่ระบุว่าให้บังคับให้ค่าคงที่ b เท่ากับ 0 หรือไม่
-
ถ้า const เป็น TRUE หรือละไว้ b จะถูกคำนวณตามวิธีปกติ
-
ถ้า const เป็น FALSE จะตั้งค่า b ให้เท่ากับ 0 และปรับค่า m ให้เหมาะกับสมการ y = mx
-
-
stats ไม่จำเป็น ค่าตรรกะที่ระบุว่าจะส่งกลับสถิติการถดถอยเพิ่มเติมหรือไม่
-
ถ้า stats เป็น TRUE แล้ว LINEST จะส่งกลับค่าสถิติการถดถอยเพิ่มเติม ดังนั้นอาร์เรย์ที่ส่งกลับคือ {mn,mn-1,...,m1,b;sen,sen-1,...,sb1,seb;r2,sey; F,df;ssreg,ssresid}.
-
ถ้า stats เป็น FALSE หรือถ้าไม่ใส่ค่าใดไว้ LINEST จะส่งกลับเฉพาะค่าสัมประสิทธิ์ m และค่าคงที่ b เท่านั้น
สถิติการถดถอยเพิ่มเติมมีดังนี้
-
|
สถิติ |
คำอธิบาย |
|---|---|
|
se1,se2,...,sen |
ค่าความผิดพลาดมาตรฐานของสัมประสิทธิ์ m1,m2,...,mn |
|
seb |
ค่าความผิดพลาดมาตรฐานของค่าคงที่ b (seb = #N/A เมื่อ const เป็น FALSE) |
|
r2 |
สัมประสิทธิ์ของการกําหนดค่า เปรียบเทียบค่า y โดยประมาณและตามจริง และช่วงที่มีค่าตั้งแต่ 0 ถึง 1 ถ้าเป็น 1 จะมีสหสัมพันธ์ที่สมบูรณ์แบบในตัวอย่าง — ไม่มีความแตกต่างระหว่างค่า y โดยประมาณกับค่า y จริง ที่ขั้วอื่น ถ้าสัมประสิทธิ์ของการกําหนดค่าเป็น 0 สมการการถดถอยจะไม่มีประโยชน์ในการคาดเดาค่า y ดูข้อมูลเกี่ยวกับวิธีการคํานวณ2 ให้ดูที่ "ข้อสังเกต" ต่อไปในหัวข้อนี้ |
|
sey |
ค่าความผิดพลาดมาตรฐานของค่าประมาณ y |
|
F |
สถิติ F หรือค่า F ที่สังเกตได้ ใช้สถิติ F เพื่อระบุว่าความสัมพันธ์ที่สังเกตได้ระหว่างตัวแปรอิสระและตัวแปรอิสระเกิดขึ้นโดยบังเอิญหรือไม่ |
|
df |
ระดับความเป็นอิสระ ใช้องศาความเป็นอิสระเพื่อช่วยให้คุณค้นหาค่าวิกฤต F ในตารางทางสถิติ เปรียบเทียบค่าที่คุณพบในตารางกับสถิติ F ที่ส่งกลับโดย LINEST เพื่อหาระดับความเชื่อมั่นของตัวแบบ ดูข้อมูลเกี่ยวกับวิธีการคํานวณ df ให้ดูที่ "ข้อสังเกต" ต่อไปในหัวข้อนี้ ตัวอย่างที่ 4 แสดงการใช้ F และ df |
|
ssreg |
ผลรวมกำลังสองที่ถดถอย |
|
ssresid |
ผลรวมสี่เหลี่ยมที่ตกค้าง For information about how ssreg and ssresid are calculated, see "Remarks, " later in this topic. |
ภาพประกอบตัวอย่างต่อไปนี้แสดงลำดับที่ส่งกลับค่าสถิติการถดถอยเพิ่มเติม
ข้อสังเกต
-
คุณสามารถอธิบายเส้นตรงด้วยความชัน และจุดตัดบนแกน y
ความชัน (m):
เมื่อต้องการหาความชันของเส้นตรง ซึ่งโดยมากจะเขียนด้วย m จะใช้จุดสองจุดบนเส้นตรง (x1,y1) และ (x2,y2) ความชันเท่ากับ (y2 - y1)/(x2 - x1)ตัวตัดกัน Y (b):
จุดตัดแกน y ของเส้นตรง ซึ่งมักจะเขียนเป็น b คือค่าของ y ณ จุดที่เส้นตรงตัดแกน yสมการของเส้นตรงคือ y = mx + b เมื่อคุณทราบค่าของ m และ b คุณสามารถคํานวณจุดใดๆ บนเส้นได้โดยการเสียบค่า y- หรือ x ลงในสมการนั้น คุณยังสามารถใช้ฟังก์ชัน TREND ได้
-
เมื่อคุณมีตัวแปร x ที่เป็นตัวแปรอิสระเพียงตัวเดียว คุณสามารถหาความชัน และจุดตัดแกน y ได้โดยตรงด้วยการใช้สูตรต่อไปนี้
ความชัน:
=INDEX(LINEST(known_y's,known_x's),1)ตัวตัดกัน Y:
=INDEX(LINEST(known_y's,known_x's),2) -
ความถูกต้องของเส้นที่คํานวณโดยฟังก์ชัน LINEST จะขึ้นอยู่กับระดับการกระจายในข้อมูลของคุณ ยิ่งข้อมูลเป็นเส้นตรงมากขึ้น ยิ่งตัวแบบ LINEST ถูกต้องมากขึ้นเท่านั้น LINEST จะใช้วิธีค่าสี่เหลี่ยมที่น้อยที่สุดในการกําหนดค่าที่เหมาะสมที่สุดกับข้อมูล เมื่อคุณมีตัวแปร x อิสระเพียงตัวเดียว การคํานวณของ m และ b จะยึดตามสูตรต่อไปนี้
เมื่อ x และ y เป็นค่าเฉลี่ยของตัวอย่าง นั่นคือ x = AVERAGE(known x's) และ y = AVERAGE(known_y's)
-
ฟังก์ชันการปรับให้พอดีบรรทัดและเส้นโค้ง LINEST และ LOGEST สามารถคํานวณเส้นตรงหรือเส้นโค้งเอ็กซ์โพเนนเชียลที่ดีที่สุดที่เหมาะกับข้อมูลของคุณ อย่างไรก็ตาม คุณต้องตัดสินใจว่าผลลัพธ์ใดของสองรายการที่เหมาะสมกับข้อมูลของคุณที่สุด คุณสามารถคํานวณTREND(known_y's,known_x's)ของเส้นตรง หรือGROWTH(known_y's, known_x's) ของเส้นโค้งเอ็กซ์โพเนนเชียล ฟังก์ชันเหล่านี้โดยไม่มีอาร์กิวเมนต์ new_xของฟังก์ชัน ให้ส่งกลับอาร์เรย์ของค่า y ที่คาดการณ์ตามเส้นหรือเส้นโค้งตรงจุดข้อมูลจริงของคุณ จากนั้น คุณสามารถเปรียบเทียบค่าที่คาดการณ์กับค่าจริงได้ คุณอาจต้องการสร้างแผนภูมิทั้งสองรายการเพื่อการเปรียบเทียบแบบเป็นภาพ
-
ในการวิเคราะห์การถดExcelจะคํานวณแต่ละจุด ผลต่างที่เป็นสี่เหลี่ยมระหว่างค่า y โดยประมาณของจุดนั้นกับค่า y จริง ผลรวมของผลต่างที่เป็นสี่เหลี่ยมจัตุรัสเหล่านี้เรียกว่า ผลรวมที่เหลือของค่าสี่เหลี่ยม ssresid Excelจะคํานวณผลรวมทั้งหมดของค่า squares, sstotal เมื่อ อาร์กิวเมนต์ const = TRUE หรือถูกละไว้ ผลรวมรวมของค่า squares คือผลรวมของผลต่างที่เป็นสี่เหลี่ยมจัตุรัสระหว่างค่า y จริงและค่าเฉลี่ยของค่า y เมื่ออาร์กิวเมนต์ const = FALSE ผลรวมทั้งหมดของค่าสี่เหลี่ยมจัตุรัสคือผลรวมของค่า y จริง (โดยไม่ลบค่าเฉลี่ยค่า y จากค่า y แต่ละค่า) จากนั้นจะพบผลรวมการถดถอยของค่าสี่เหลี่ยม, ssreg จาก: ssreg = sstotal - ssresid ยิ่งค่าผลรวมเหลือของค่าสี่เหลี่ยมเหลือน้อยกว่าคือเมื่อเปรียบเทียบกับผลรวมทั้งหมดของค่าสี่เหลี่ยมจัตุรัส ค่าสัมประสิทธิ์ของการกําหนดค่า r2ยิ่งเป็นตัวบ่งชี้ของสมการที่เป็นผลมาจากการวิเคราะห์การถดถอยยิ่งดีเท่าใด จะอธิบายความสัมพันธ์ระหว่างตัวแปรต่างๆ ค่าของ r2 เท่ากับ ssreg/sstotal
-
ในบางกรณี คอลัมน์ X อย่างน้อยหนึ่งคอลัมน์ (สมมติว่า Y และ X อยู่ในคอลัมน์) อาจไม่มีค่าการคาดการณ์เพิ่มเติมในการแสดงตนของคอลัมน์ X อื่นๆ กล่าวคือ การกรอคอลัมน์ X อย่างน้อยหนึ่งคอลัมน์อาจไปสู่การคาดเดาค่า Y ที่มีความถูกต้องเท่ากัน ในกรณีนี้ คอลัมน์ X ที่ซ้.มกันเหล่านี้ควรถูกละเว้นจากตัวแบบการถดถอย อันนี้เรียกว่า "collinearity" เนื่องจากคอลัมน์ X ที่ซ้าซ้อนใดๆ สามารถแสดงเป็นผลรวมของพยคูณของคอลัมน์ X ที่ไม่ซ้ากันได้ ฟังก์ชัน LINEST จะตรวจสอบหาค่าความบกพร่องในเส้นตรง และเอาคอลัมน์ X ที่ซ้่าซ้อนใดๆ ออกจากตัวแบบการถดถอยเมื่อระบุคอลัมน์เหล่านั้น คอลัมน์ Removed X สามารถถูกรับรู้ใน ผลลัพธ์ของ LINEST ว่ามีค่าสัมประสิทธิ์ 0 บวกกับ 0 ค่า se ถ้าคอลัมน์อย่างน้อยหนึ่งคอลัมน์ถูกเอาออกเป็นคอลัมน์ซ้่ากัน df จะได้รับผลกระทบเนื่องจาก df ขึ้นอยู่กับจํานวนคอลัมน์ X ที่ใช้จริงเพื่อวัตถุประสงค์ในการคาดเดา For details on the computation of df, see Example 4. ถ้า df ถูกเปลี่ยนแปลงเนื่องจากคอลัมน์ X ที่ซ้าซ้อนถูกเอาออก ค่าของ sey และ F จะได้รับผลกระทบด้วย Collinearity ควรค่อนข้างพบได้ยากในการฝึกปฏิบัติ อย่างไรก็ตาม กรณีหนึ่งที่มีแนวโน้มที่จะเกิดขึ้นคือเมื่อคอลัมน์ X บางคอลัมน์มีค่าเพียง 0 และ 1 เป็นตัวบ่งชี้ว่าเรื่องในการทดลองเป็นสมาชิกของกลุ่มใดกลุ่มหนึ่งหรือไม่ ถ้า const = TRUE หรือถูกละไว้ ฟังก์ชัน LINEST จะแทรกคอลัมน์ X เพิ่มเติมของค่า 1 ทั้งหมดอย่างมีประสิทธิภาพเพื่อโมเดลการตัดแกน ถ้าคุณมีคอลัมน์ที่มี 1 ของหัวข้อแต่ละเรื่องถ้าเป็นเพศชาย หรือ 0 ถ้าไม่ใช่ และคุณมีคอลัมน์ที่มี 1 เป็น 1 ในแต่ละหัวข้อถ้าเป็นผู้หญิง หรือ 0 ถ้าไม่ใช่ คอลัมน์หลังนี้ฟ้ดซ้อนเนื่องจากรายการในนั้นสามารถมาจากการลบรายการในคอลัมน์ "ตัวบ่งชี้ตัวผู้" จากรายการในคอลัมน์เพิ่มเติมของค่า 1 ทั้งหมดที่ถูกเพิ่มโดยฟังก์ชันLINEST
-
ค่าของ df จะถูกคํานวณดังนี้ เมื่อไม่มีเอาคอลัมน์ X ออกจากตัวแบบเนื่องจากเส้นตรง ถ้ามีคอลัมน์ k ของ known_x และ const = TRUE หรือละไว้ df = n – k – 1 ถ้า const = FALSE, df = n - k ในทั้งสองกรณี คอลัมน์ X แต่ละคอลัมน์ถูกเอาออกเนื่องจากเส้นตรงจะเพิ่มค่าของ df ขึ้น 1
-
เมื่อใส่ค่าคงที่อาร์เรย์ (เช่น known_x's) เป็นอาร์กิวเมนต์ ให้ใช้เครื่องหมายจุลภาคคั่นระหว่างค่าที่อยู่ในแถวเดียวกัน และใช้เครื่องหมายอัฒภาคเพื่อแยกแถว อักขระตัวคั่นอาจแตกต่างกันโดยขึ้นอยู่กับการตั้งค่าภูมิภาคของคุณ
-
จงจำไว้ว่าค่า y จากการทำนายโดยสมการการถดถอยอาจไม่ถูกต้องถ้าอยู่นอกช่วงของค่า y ที่คุณใช้กำหนดสมการ
-
อัลกอริทึมที่ถูกใช้ในฟังก์ชันLINESTนั้นแตกต่างจากอัลกอริทึมพื้นฐานที่ใช้ในฟังก์ชันSLOPEและ INTERCEPT ความแตกต่างระหว่างอัลกอริทึมเหล่านี้อาจไปสู่ผลลัพธ์ที่แตกต่างกันเมื่อไม่ได้ระบุข้อมูลและข้อมูลที่เกี่ยวข้อง ตัวอย่างเช่น ถ้าจุดข้อมูลของอาร์กิวเมนต์ของ known_y คือ 0 และจุดข้อมูลของอาร์กิวเมนต์ known_x คือ 1:
-
LINEST ส่งกลับค่า 0 อัลกอริทึมของฟังก์ชัน LINEST ถูกออกแบบมาเพื่อให้ส่งกลับผลลัพธ์ที่สมเหตุสมผลของข้อมูล Collinear และในกรณีนี้สามารถพบได้อย่างน้อยหนึ่งคําตอบ
-
SLOPE และ INTERCEPT จะ ส่งกลับค่า #DIV/0! ข้อผิดพลาด อัลกอริทึมของฟังก์ชัน SLOPEและ INTERCEPT ถูกออกแบบมาเพื่อค้นหาคําตอบเพียงคําตอบเดียว และในกรณีนี้อาจมีคําตอบได้มากกว่าหนึ่งคําตอบ
-
-
นอกจากการใช้LOGESTเพื่อคํานวณสถิติของชนิดการถดถอยอื่น แล้ว คุณสามารถใช้LINESTเพื่อคํานวณช่วงของชนิดการถดถอยอื่นๆ โดยการใส่ฟังก์ชันของตัวแปร x และ y เป็นชุดข้อมูล x และ y ของLINEST ตัวอย่างเช่น สูตรต่อไปนี้
=LINEST(yvalues, xvalues^COLUMN($A:$C))
จะทำงานเมื่อคุณมีคอลัมน์เดียวของค่า y และคอลัมน์เดียวของค่า x เพื่อคำนวณค่าประมาณ (โพลิโนเมียลอันดับ 3) แบบลูกบาศก์ของฟอร์ม
y = m1*x + m2*x^2 + m3*x^3 + b
คุณสามารถปรับสูตรนี้เพื่อคำนวณการถดถอยชนิดอื่นได้ แต่ในบางกรณีจำเป็นที่จะต้องปรับค่าผลลัพธ์และสถิติอื่นด้วย
-
ค่า F-test ที่ส่งกลับโดยฟังก์ชัน LINEST แตกต่างจากค่า F-test ที่ส่งกลับโดยฟังก์ชัน FTEST LINEST จะส่งกลับค่าสถิติ F ในขณะที่ FTEST จะส่งกลับความน่าจะเป็น
ตัวอย่าง
ตัวอย่าง 1 - ความชันและจุดตัดแกน Y
คัดลอกข้อมูลตัวอย่างในตารางต่อไปนี้ และวางในเซลล์ A1 ของเวิร์กชีต Excel ใหม่ เพื่อให้สูตรแสดงผลลัพธ์ ให้เลือกสูตร กด F2 แล้วกด Enter ถ้าคุณต้องการ คุณสามารถปรับความกว้างของคอลัมน์เพื่อดูข้อมูลทั้งหมดได้
|
ค่า y ที่ทราบแล้ว |
ค่า x ที่ทราบแล้ว |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
ผลลัพธ์ (ความชัน) |
ผลลัพธ์ (จุดตัดแกน y) |
|
2 |
1 |
|
สูตร (สูตรอาร์เรย์ในเซลล์ A7:B7) |
|
|
=LINEST(A2:A5,B2:B5,,FALSE) |
ตัวอย่าง 2 - การถดถอยเชิงเส้นแบบเชิงเดียว
คัดลอกข้อมูลตัวอย่างในตารางต่อไปนี้ และวางในเซลล์ A1 ของเวิร์กชีต Excel ใหม่ เพื่อให้สูตรแสดงผลลัพธ์ ให้เลือกสูตร กด F2 แล้วกด Enter ถ้าคุณต้องการ คุณสามารถปรับความกว้างของคอลัมน์เพื่อดูข้อมูลทั้งหมดได้
|
เดือน |
ยอดขาย |
|---|---|
|
1 |
$3,100 |
|
2 |
$4,500 |
|
3 |
$4,400 |
|
4 |
$5,400 |
|
5 |
$7,500 |
|
6 |
$8,100 |
|
สูตร |
ผลลัพธ์ |
|
=SUM(LINEST(B1:B6, A1:A6)*{9,1}) |
$11,000 |
|
คำนวณค่าประมาณของยอดขายในเดือนที่เก้า โดยใช้ยอดขายในเดือนที่ 1 ถึงเดือนที่ 6 |
ตัวอย่าง 3 - การถดถอยเชิงเส้นแบบพหุคูณ
คัดลอกข้อมูลตัวอย่างในตารางต่อไปนี้ และวางในเซลล์ A1 ของเวิร์กชีต Excel ใหม่ เพื่อให้สูตรแสดงผลลัพธ์ ให้เลือกสูตร กด F2 แล้วกด Enter ถ้าคุณต้องการ คุณสามารถปรับความกว้างของคอลัมน์เพื่อดูข้อมูลทั้งหมดได้
|
พื้นที่ของชั้น (x1) |
สำนักงาน (x2) |
ทางเข้า (x3) |
อายุ (x4) |
ค่าที่ประเมินได้ (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
$142,000 |
|
2333 |
2 |
2 |
1.2 |
$144,000 |
|
2356 |
3 |
1.5 |
33 |
$151,000 |
|
2379 |
3 |
2 |
43 |
$150,000 |
|
2402 |
2 |
3 |
53 |
$139,000 |
|
2425 |
4 |
2 |
23 |
$169,000 |
|
2448 |
2 |
1.5 |
99 |
$126,000 |
|
2471 |
2 |
2 |
34 |
$142,900 |
|
2494 |
3 |
3 |
23 |
$163,000 |
|
2517 |
4 |
4 |
55 |
$169,000 |
|
2540 |
2 |
3 |
22 |
$149,000 |
|
-234.2371645 |
||||
|
13.26801148 |
||||
|
0.996747993 |
||||
|
459.7536742 |
||||
|
1732393319 |
||||
|
สูตร (สูตรอาร์เรย์แบบไดนามิกที่ใส่ใน A19) |
||||
|
=LINEST(E2:E12,A2:D12,TRUE,TRUE) |
ตัวอย่างที่ 4 - การใช้สถิติ F และ r2
ในตัวอย่างก่อนหน้า สัมประสิทธิ์ของการกําหนดค่า หรือ r2คือ 0.99675 (ดูเซลล์ A17 ในผลลัพธ์ที่ LINEST) ซึ่งจะระบุความสัมพันธ์ที่มากระหว่างตัวแปรอิสระและราคาขาย คุณสามารถใช้สถิติ F เพื่อพิจารณาว่าจะให้ผลลัพธ์เหล่านี้ มีค่า r2 สูงเช่นนี้เกิดขึ้นโดยบังเอิญหรือไม่
สมมติว่าตัวแปรเหล่านี้ไม่มีความสัมพันธ์ต่อกัน แต่คุณได้สุ่มตัวอย่างของอาคารสํานักงาน 11 หลังที่ก่อให้เกิดการวิเคราะห์ทางสถิติเพื่อแสดงความสัมพันธ์ที่รัดกุม the term "Alpha" is used for the probability of erronaously concluding that there is a relationship.
ค่า F และ df ในผลลัพธ์จากฟังก์ชัน LINEST สามารถใช้เพื่อประเมินความน่าจะเป็นของค่า F ที่สูงขึ้นที่เกิดขึ้นโดยบังเอิญ F สามารถเปรียบเทียบกับค่าวิกฤตในตารางการแจกแจง F หรือฟังก์ชันFDISTใน Excel เพื่อคํานวณความน่าจะเป็นของค่า F ที่มีค่า F ที่มากขึ้นที่เกิดขึ้นโดยบังเอิญ การแจกแจง F ที่เหมาะสมมีระดับความเป็นอิสระ v1 และ v2 ถ้า n เป็นจํานวนจุดข้อมูลและ const = TRUE หรือละไว้ จะ v1 = n – df – 1 และ v2 = df (ถ้า const = FALSE แล้ว v1 = n – df และ v2 = df) ฟังก์ชัน FDIST ที่มีไวยากรณ์ FDIST(F,v1,v2) จะส่งกลับความน่าจะเป็นของค่า F ที่สูงขึ้นที่เกิดขึ้นโดยบังเอิญ ในตัวอย่างนี้ df = 6 (เซลล์ B18) และ F = 459.753674 (เซลล์ A18)
สมมติว่าค่า Alpha เป็น 0.05, v1 = 11 – 6 – 1 = 4 และ v2 = 6 ระดับวิกฤตของ F คือ 4.53 เนื่องจาก F = 459.753674 มีค่าสูงกว่า 4.53 มาก ไม่น่าเป็นไปได้มากที่ค่า F นี้เกิดขึ้นโดยบังเอิญ (ด้วย Alpha = 0.05 สมมติฐานว่าไม่มีความสัมพันธ์ระหว่าง known_y และ known_x คือการปฏิเสธเมื่อ F เกินระดับวิกฤตคือ 4.53) คุณสามารถใช้ฟังก์ชันFDISTในการExcelความน่าจะเป็นที่ค่า F ที่ค่าสูงนี้เกิดขึ้นโดยบังเอิญ ตัวอย่างเช่น FDIST(459.753674, 4, 6) = 1.37S-7 ความน่าจะเป็นที่เล็กมาก คุณสามารถสรุปได้ ไม่ว่าจะโดยการค้นหาระดับวิกฤตของ F ในตาราง หรือโดยใช้ฟังก์ชัน FDIST สมการการถดถอยมีประโยชน์ในการคาดเดาค่าประเมินของอาคารสํานักงานในพื้นที่นี้ โปรดทราบว่า การใช้ค่าที่ถูกต้องของ v1 และ v2 ที่ถูกประมวลผลในย่อหน้าก่อนหน้านั้นคือสิ่งที่ต้องระบุ
ตัวอย่าง 5 - การคำนวณสถิติ t
การทดสอบสมมติฐานอื่นจะระบุว่าสัมประสิทธิ์ความชันชันแต่ละค่ามีประโยชน์ในการประมาณค่าประเมินของอาคารสํานักงานใน ตัวอย่างที่ 3หรือไม่ ตัวอย่างเช่น เมื่อต้องการทดสอบสัมประสิทธิ์อายุตามนัยทางสถิติ ให้หาร -234.24 (สัมประสิทธิ์ความชันอายุ) ด้วย 13.268 (ค่าผิดพลาดมาตรฐานโดยประมาณของสัมประสิทธิ์อายุในเซลล์ A15) ต่อไปนี้คือค่า t-observed:
t = m4 ÷ se4 = -234.24 ÷ 13.268 = -17.7
ถ้าค่าสัมบูรณ์ของ t มีค่าสูงพอ จะสามารถสรุปได้ว่าค่าสัมประสิทธิ์ความชันจะมีประโยชน์ในการประมาณค่าประเมินของอาคารสํานักงานในตัวอย่างที่ 3 ตารางต่อไปนี้แสดงค่าสัมบูรณ์ของค่า t 4 ค่าที่สังเกตได้
ถ้าคุณดูตารางในคู่มือสถิติ คุณจะพบว่าไม่ร้ายแรง ด้านสองด้าน ที่มี 6 ระดับความเป็นอิสระ และ Alpha = 0.05 คือ 2.447 นอกจากนี้ยังสามารถพบค่าวิกฤตนี้ได้โดยใช้ฟังก์ชันTINVในExcel TINV(0.05,6) = 2.447 เนื่องจากค่าสัมบูรณ์ของ t (17.7) มากกว่า 2.447 อายุเป็นตัวแปรที่สําคัญเมื่อประเมินค่าประเมินของอาคารสํานักงาน แต่ละตัวแปรอิสระอื่นๆ สามารถทดสอบตามนัยทางสถิติในลักษณะที่คล้ายกัน ต่อไปนี้คือค่า t-observed ของแต่ละตัวแปรอิสระ
|
ตัวแปร |
ค่า t ที่ได้จากการสังเกต |
|---|---|
|
พื้นที่ของชั้น |
5.1 |
|
จำนวนสำนักงาน |
31.3 |
|
จำนวนทางเข้า |
4.8 |
|
อายุ |
17.7 |
ค่าเหล่านี้ล้วนมีค่าสัมบูรณ์ที่มากกว่า 2.447 ดังนั้น ตัวแปรทั้งหมดที่ใช้ในสมการการถดถอยจึงเป็นประโยชน์ในการประมาณค่าประเมินของอาคารสำนักงานในพื้นที่นี้
