Увага!: Підтримка Office 2016 і Office 2019 завершиться 14 жовтня 2025 р. Оновіть до версії Microsoft 365, щоб працювати будь-де з будь-якого пристрою та продовжуйте отримувати підтримку. Отримати Microsoft 365
У цій статті описано використання надбудови "Пошук розв'язання" (Microsoft Excel), яку можна використовувати для аналізу "what-if", щоб визначити оптимальну суміш продукту.
Як визначити щомісячну суміш продукту, яка збільшує рентабельність?
Компаніям часто потрібно щомісяця визначати кількість кожного продукту. У найпростішому вигляді проблема суміші продукту включає в себе, як визначити кількість кожного продукту, який повинен бути вироблений протягом місяця, щоб максимізувати прибуток. Суміш продукту зазвичай має дотримуватися таких обмежень:
-
У суміші продуктів не можна використовувати більше ресурсів, ніж доступно.
-
Існує обмежений попит на кожен продукт. Ми не можемо виробляти більше продукту протягом місяця, ніж диктує попит, тому що надлишок виробництва даремно (наприклад, швидкопсувний препарат).
Тепер давайте вирішимо наведений нижче приклад проблеми з сумішшю продукту. Вирішення цієї проблеми можна знайти у файлі Prodmix.xlsx, як показано на рисунку 27-1.
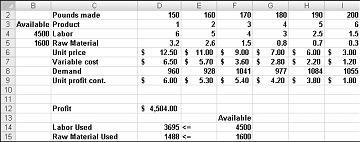
Скажімо, ми працюємо на наркокомпанія, яка виробляє шість різних продуктів на своєму заводі. Виробництво кожного продукту потребує трудової та сировини. Рядок 4 на рисунку 27-1 показує години праці, необхідні для виробництва фунта кожного продукту, а рядок 5 показує фунти сировини, необхідної для виробництва фунта кожного продукту. Наприклад, для виробництва фунта продукту 1 потрібно шість годин праці і 3,2 фунта сировини. Для кожного препарату ціна за фунт дається в рядку 6, вартість одиниці за фунт надається в рядку 7, а прибуток за фунт дається в рядку 9. Наприклад, продукт 2 продається за $ 11,00 за фунт, понесений за одиницю вартості $ 5,70 за фунт, і вносить $ 5.30 прибутку за фунт. Місячний попит на кожен препарат надається в рядку 8. Наприклад, попит на продукт 3 становить 1041 фунт. Цього місяця доступно 4500 годин праці та 1600 фунтів сировини. Як ця компанія може максимально збільшити свій щомісячний прибуток?
Якби ми нічого не знали про надбудову Excel Solver, ми атакуємо цю проблему, створюючи аркуш для відстеження прибутку та використання ресурсів, пов'язаних із сумішшю продукту. Тоді ми будемо використовувати проб і помилок, щоб варіювати суміш продукту для оптимізації прибутку, не використовуючи більше праці або сировини, ніж доступно, і без виробництва будь-якого препарату, що перевищує попит. Надбудова "Пошук розв'язання" використовується лише на стадії ознайомлення та помилки. По суті, "Пошук розв'язання" – це засіб оптимізації, який бездоганно виконує пошук за допомогою ознайомлювальної версії та помилок.
Ключем до вирішення проблеми з сумішшю продукту є ефективне обчислення використання ресурсів і прибутку, пов'язаних із будь-яким заданим поєднанням продуктів. Важливим інструментом, який можна використовувати для цього обчислення, є функція SUMPRODUCT. Функція SUMPRODUCT перемножує відповідні значення в діапазонах клітинок і повертає суму цих значень. Кожен діапазон клітинок, використовуваний для обчислення SUMPRODUCT, має мати однакові розміри, що означає, що можна використовувати SUMPRODUCT із двома рядками або двома стовпцями, але не з одним стовпцем і одним рядком.
Наприклад, як використовувати функцію SUMPRODUCT у нашому прикладі поєднання продуктів, давайте спробуємо обчислити використання ресурсів. Наше трудове використання обчислюється
(Праця використовується на фунт наркотику 1)*(Наркотики 1 фунтів вироблено)+ (Праця використовується на фунт наркотиків 2)*(Наркотики 2 фунтів вироблено) + ... (Праця використовується за фунт наркотиків 6)*(Наркотики 6 фунтів вироблено)
Ми могли б обчислити використання праці в більш втомливим чином, як D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Аналогічно, використання сировини можна обчислити як D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Однак введення цих формул на аркуші для шести продуктів займає багато часу. Уявіть собі, скільки часу знадобилося б, якби ви працювали з компанією, яка виробляла, наприклад, 50 товарів на своєму заводі. Набагато простіший спосіб обчислити використання робочої сили та сировини – скопіювати з D14 до D15 формулу SUMPRODUCT($D$2:$I$2;D4:I4). Ця формула обчислює D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (це наше трудове використання), але набагато простіше ввести! Зверніть увагу, що я використовую знак $ з діапазоном D2:I2, так що, коли я копіюю формулу я все ще записую суміш продукту з рядка 2. Формула в клітинці D15 обчислює використання сировини.
Подібним чином наш прибуток визначається
(Препарат 1 прибуток за фунт)*(Препарат 1 фунт вироблено) + (Наркотики 2 прибутку за фунт)*(Наркотики 2 фунтів вироблено) + ... (Препарат 6 прибуток за фунт)*(Наркотики 6 фунтів вироблено)
Прибуток легко обчислюється в клітинці D12 за допомогою формули SUMPRODUCT(D9:I9,$D$2:$I$2).
Тепер ми можемо визначити три компоненти нашої моделі надбудови "Пошук розв'язання".
-
Цільова клітинка. Наша мета – максимально збільшити прибуток (обчислюється в клітинці D12).
-
Змінювані клітинки. Кількість фунтів стерлінгів кожного продукту (зазначена в діапазоні клітинок D2:I2)
-
Обмежень. У нас є такі обмеження:
-
Не використовуйте більше робочої сили або сировини, ніж є. Тобто значення в клітинках D14:D15 (використовувані ресурси) мають бути меншими або дорівнювати значенням у клітинках F14:F15 (наявні ресурси).
-
Не виробляти більше препарату, ніж користується попитом. Тобто значення в клітинках D2:I2 (фунти, вироблені з кожного препарату) повинні бути меншими або дорівнювати попиту на кожен препарат (перелічені в клітинках D8:I8).
-
Ми не можемо виробляти від'ємну кількість будь-якого препарату.
-
Я покажу вам, як вводити цільову клітинку, змінювати клітинки та обмеження в надбудові "Пошук розв'язання". Тоді все, що вам потрібно зробити, це натиснути кнопку "Розв'язати", щоб знайти суміш продукту, що максимізує прибуток!
Щоб почати, перейдіть на вкладку Дані та в групі Аналіз натисніть кнопку Пошук розв'язання.
Примітка.: Як описано в розділі 26 "Загальні відомості про оптимізацію за допомогою розв'язувача Excel", надбудову інстальовано, натиснувши кнопку Microsoft Office, а потім – параметри Excel, а потім – надбудови. У списку Керування виберіть пункт Надбудови Excel, установіть прапорець Надбудова "Пошук розв'язання" та натисніть кнопку OK.
Відкриється діалогове вікно Параметри розв'язувача, як показано на рисунку 27-2.
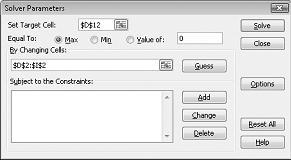
Клацніть поле Установити цільову клітинку, а потім виберіть нашу клітинку прибутку (клітинка D12). Клацніть поле За змінюваними клітинками, а потім наведіть вказівник миші на діапазон D2:I2, який містить фунти, вироблені з кожного препарату. Тепер діалогове вікно має виглядати на рисунку 27-3.
Тепер ми готові додати обмеження до моделі. Натисніть кнопку Додати. Відкриється діалогове вікно Додавання обмеження, показане на рисунку 27–4.
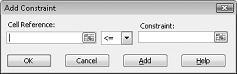
Щоб додати обмеження використання ресурсів, клацніть поле Посилання на клітинку, а потім виберіть діапазон D14:D15. Виберіть <= в середньому списку. Клацніть поле Обмеження, а потім виберіть діапазон клітинок F14:F15. Тепер діалогове вікно Додавання обмеження має виглядати як Рисунок 27-5.
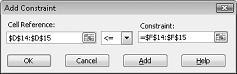
Тепер ми гарантуємо, що, коли надбудова "Пошук розв'язання" намагається використовувати різні значення для змінюваних клітинок, розглядатимуться лише комбінації, які задовольняють обидві функції D14<=F14 (використана робоча сила менша або рівна доступній праці) і D15<=F15 (сировина, яка використовується, менша або дорівнює доступній сировині). Натисніть кнопку Додати, щоб ввести обмеження на вимогу. Заповніть діалогове вікно Додавання обмеження, як показано на рисунку 27–6.
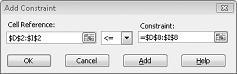
Додавання цих обмежень гарантує, що, коли надбудова "Пошук розв'язання" намагається використовувати різні комбінації для змінюваних значень клітинок, розглядатимуться лише комбінації, які відповідають таким параметрам:
-
D2<=D8 (кількість, вироблена препаратом 1, менша або дорівнює попиту на препарат 1)
-
E2<=E8 (кількість виробленого препарату 2 менша або дорівнює попиту на препарат 2)
-
F2<=F8 (кількість виготовлених препаратів 3 менша або дорівнює попиту на препарат 3)
-
G2<=G8 (кількість виготовлених препаратів 4 менша або дорівнює попиту на препарат 4)
-
H2<=H8 (кількість виготовлених препаратів 5 менша або дорівнює попиту на препарат 5)
-
I2<=I8 (кількість вироблених препаратів 6 менша або дорівнює попиту на препарат 6)
У діалоговому вікні Додавання обмеження натисніть кнопку OK. Вікно "Пошук розв'язання" має виглядати як рисунок 27-7.
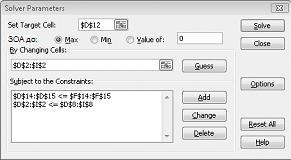
У діалоговому вікні Параметри розв'язувача ми введемо обмеження, що змінювані клітинки мають бути не від'ємними. Натисніть кнопку Параметри в діалоговому вікні Параметри розв'язувача. Установіть прапорці Припускати лінійну модель і Припускати не від'ємні значення, як показано на рисунку 27-8 на наступній сторінці. Натисніть кнопку OK.
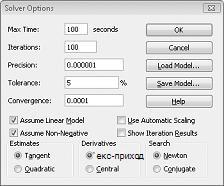
Якщо встановити прапорець Не від'ємне значення, надбудова "Пошук розв'язання" обчислює лише комбінації змінюваних клітинок, у яких кожна змінювана клітинка має не від'ємне значення. Ми перевірили поле Модель лінійного припущення, тому що проблема з сумішшю продукту – це особливий тип проблеми розв'язувача, яка називається лінійною моделлю. По суті, модель розв'язувача лінійна за таких умов:
-
Цільова клітинка обчислюється, додаючи разом умови форми (змінювана клітинка)*(константа).
-
Кожне обмеження відповідає "лінійній вимозі моделі". Це означає, що кожне обмеження обчислюється шляхом об'єднання умов форми (змінення клітинки)*(константи) і порівняння сум із константою.
Чому ця проблема розв'язувача лінійна? Наша цільова клітинка (прибуток) обчислюється як
(Препарат 1 прибуток за фунт)*(Препарат 1 фунт вироблено) + (Наркотики 2 прибутку за фунт)*(Наркотики 2 фунтів вироблено) + ... (Препарат 6 прибуток за фунт)*(Наркотики 6 фунтів вироблено)
Це обчислення відповідає шаблону, у якому значення цільової клітинки походить від додавання разом термінів форми (змінювана клітинка)*(константа).
Наше обмеження праці оцінюється шляхом порівняння значення, отриманого з (Праці використовується на фунт наркотиків 1)*(Наркотики 1 фунтів вироблено) + (Праці використовується за фунт наркотиків 2)*(Наркотики 2 фунтів вироблено)+ ... (Працюйте з нами)ed за фунт наркотиків 6)*(Наркотики 6 фунтів вироблено) до праці доступні.
Таким чином, обмеження робочої сили обчислюється шляхом об'єднання умов форми (змінювана клітинка)*(константа) і порівняння сум з константою. Обмеження робочої сили та обмеження сировини задовольняють вимогу лінійної моделі.
Наші обмеження попиту набирають форму
(Препарат 1 вироблено)<=(Препарат 1 Попит) (Препарат 2 вироблено)<=(Препарат 2 Попит) §(Препарат 6 вироблено)<=(Препарат 6 Попит)
Кожне обмеження вимоги також задовольняє вимоги лінійної моделі, оскільки кожне з них обчислюється додаванням разом умов форми (змінення клітинки)*(константи) і порівнянням сум із константою.
Показавши, що наша модель суміші продукту є лінійною моделлю, чому ми повинні піклуватися?
-
Якщо модель надбудови "Пошук розв'язання" лінійна, а ми вибираємо Варіант лінійної моделі, надбудова "Пошук розв'язання" гарантовано знайде оптимальне рішення для моделі "Пошук розв'язання". Якщо модель розв'язувача не лінійна, надбудова "Пошук розв'язання" може знайти оптимальне рішення або не знайти його.
-
Якщо модель розв'язувача лінійна і ми вибираємо Команду "Припустити лінійну модель", надбудова "Пошук розв'язання" використовує дуже ефективний алгоритм (простий метод), щоб знайти оптимальне рішення моделі. Якщо модель розв'язувача лінійна і ми не вибираємо Команду "Припустити лінійну модель", надбудова "Пошук розв'язання" використовує дуже неефективний алгоритм (метод GRG2) і може мати труднощі з пошуком оптимального рішення моделі.
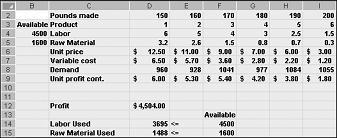
Натиснувши кнопку OK у діалоговому вікні Параметри розв'язувача, ми повернемося до головного діалогового вікна Пошук розв'язання, показаного вище на рисунку 27-7. Якщо натиснути кнопку Розв'язати, надбудова "Пошук розв'язання" обчислює оптимальне рішення (якщо це існує) для нашої моделі поєднання продуктів. Як я вже заявляв у Розділі 26, оптимальним рішенням моделі суміші продукту буде набір змінних значень клітин (фунтів, вироблених з кожного препарату), що максимізує прибуток над набором всіх можливих рішень. Знову ж таки, можливим рішенням є набір змінюваних значень клітинок, що задовольняють усі обмеження. Змінювані значення клітинок, показані на рисунку 27-9, є можливим рішенням, оскільки всі рівні виробництва не від'ємні, рівень виробництва не перевищує попит, а використання ресурсів не перевищує доступних ресурсів.
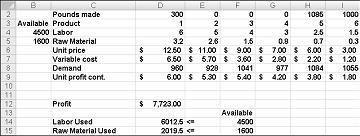
Змінювані значення клітинок, показані на рисунку 27-10 на наступній сторінці, відповідають нездійсненному рішенню з таких причин:
-
Ми виробляємо більше наркотиків 5, ніж попит на нього.
-
Ми використовуємо більше праці, ніж доступно.
-
Ми використовуємо більше сировини, ніж є.
Натиснувши кнопку Розв'язати, надбудова "Пошук розв'язання" швидко знаходить оптимальне рішення, показане на рисунку 27–11. Щоб зберегти оптимальні значення розв'язання на аркуші, потрібно вибрати елемент Зберегти розв'язання розв'язання.
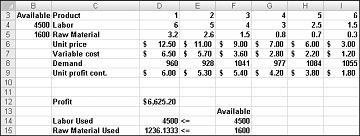
Наша наркокомпанія може максимізувати свій щомісячний прибуток на рівні $ 6625,20, виробляючи 596,67 фунтів наркотиків 4, 1084 фунтів наркотиків 5, і жоден з інших препаратів! Ми не можемо визначити, чи зможемо ми досягти максимального прибутку в розмірі $ 6625,20 іншими способами. Все, що ми можемо бути впевнені в тому, що з нашими обмеженими ресурсами і попитом, немає ніякого способу зробити більше $ 6627,20 в цьому місяці.
Припустімо, що потреба в кожному продукті має бути виконана. (Див. аркуш "Немає можливого рішення " у файлі Prodmix.xlsx).) Після цього потрібно змінити обмеження попиту з D2:I2<=D8:I8 на D2:I2>=D8:I8. Для цього відкрийте надбудову "Пошук розв'язання", виберіть обмеження D2:I2<=D8:I8 і натисніть кнопку Змінити. Відкриється діалогове вікно Змінення обмеження, показане на рисунку 27–12.
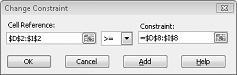
Виберіть >=, а потім натисніть кнопку OK. Тепер ми гарантуємо, що надбудова "Пошук розв'язання" розгляне можливість змінення лише значень клітинок, які відповідають усім вимогам. Якщо натиснути кнопку Розв'язати, з'явиться повідомлення "Пошук розв'язання не вдалося знайти потрібне рішення". Це повідомлення не означає, що ми зробили помилку в своїй моделі, але з обмеженими ресурсами ми не можемо задовольнити попит на всі продукти. Розв'язувач просто говорить нам, що якщо ми хочемо задовольнити попит на кожен продукт, нам потрібно додати більше праці, більше сировини, або більше обох.
Давайте подивимося, що станеться, якщо ми дозволимо необмежений попит на кожен продукт, і ми дозволяємо негативні кількості будуть вироблятися з кожного препарату. (Ця проблема з розв'язувачем відображається на аркуші Set Values Do Not Converge (Установити значення не сходиться ) у файлі Prodmix.xlsx).) Щоб знайти оптимальне рішення для цієї ситуації, відкрийте надбудову "Пошук розв'язання", натисніть кнопку Параметри та зніміть прапорець Не від'ємне значення. У діалоговому вікні Параметри розв'язувача виберіть обмеження вимоги D2:I2<=D8:I8 і натисніть кнопку Видалити, щоб видалити обмеження. Якщо натиснути кнопку Розв'язати, функція "Пошук розв'язання" поверне повідомлення "Установити значення клітинок не сходяться". Це повідомлення означає, що якщо цільову клітинку потрібно розгорнути (як у нашому прикладі), існують можливі рішення зі значеннями довільно великих цільових клітинок. (Якщо цільову клітинку потрібно згорнути, повідомлення "Установити значення клітинок не сходяться" означає, що існують можливі рішення зі значеннями довільно малих цільових клітинок.) У нашій ситуації, дозволяючи негативне виробництво препарату, ми фактично "створюємо" ресурси, які можуть бути використані для виробництва довільно великих обсягів інших препаратів. З огляду на наш необмежений попит, це дозволяє нам робити необмежений прибуток. У реальній ситуації ми не можемо заробити нескінченну суму грошей. Коротше кажучи, якщо відображається повідомлення "Установити значення не сходяться", у вашій моделі станеться помилка.
-
Припустімо, наша наркокомпанія може придбати до 500 годин праці на $1 більше на годину, ніж поточні трудовитрати. Як ми можемо максимізувати прибуток?
-
На заводі з виробництва мікросхем чотири техніки (A, B, C і D) виробляють три вироби (Продукція 1, 2 і 3). Цього місяця виробник мікросхеми може продати 80 одиниць товару 1, 50 одиниць продукту 2, а також щонайменше 50 одиниць товару 3. Технік А може зробити тільки Продукти 1 і 3. Технік Б може зробити тільки Продукти 1 і 2. Технік C може зробити тільки продукт 3. Технік D може зробити тільки продукт 2. Для кожної продукції, виробленої, продукція отримує такий прибуток: Продукт 1, $6; Товар 2, $7; і продукт 3, $ 10. Час (у годинах) кожен технік повинен виробляти продукт, як це відбувається:
Продукт
Технік А
Технічний спеціаліст Б
Технічний спеціаліст В
Технічний спеціаліст D
1
2
2,5
Не вдалося виконати
Не вдалося виконати
2
Не вдалося виконати
3
Не вдалося виконати
3,5
3
3
Не вдалося виконати
4
Не вдалося виконати
-
Кожен технік може працювати до 120 годин на місяць. Як виробник мікросхеми може максимально збільшити свій щомісячний прибуток? Припустімо, що можна виготовити дробову кількість одиниць.
-
Завод з виробництва комп'ютерів виробляє миші, клавіатури та джойстики для відеоігр. Прибуток за одиницю, використання робочої сили за одиницю, щомісячний попит і одноразове використання комп'ютера наведено в таблиці нижче.
Миша
Клавіатура
Джойстики
Прибуток/одиниця
$8
$11
$9
Трудове використання/одиниця
0,2 години
0,3 години
0,24 години
Час/одиниця комп'ютера
0,04 години
.055 год.
0,04 години
Щомісячний попит
15 000
27,000
11,000
-
Щомісяця в цілому доступно 13 000 робочих годин і 3000 годин машинного часу. Як виробник може максимально збільшити свій щомісячний прибуток від заводу?
-
Вирішити наш приклад наркотиків припускаючи, що мінімальний попит 200 одиниць для кожного препарату повинні бути виконані.
-
Джейсон робить діамантові браслети, намиста і сережки. Він хоче працювати не більше 160 годин на місяць. У нього 800 унцій діамантів. Прибуток, трудовий час і унції алмазів, необхідних для виробництва кожного продукту даються нижче. Якщо попит на кожен продукт необмежений, як Джейсон може максимізувати свій прибуток?
Продукт
Прибуток за одиницю
Трудові години на одиницю
Унції ромбів на одиницю
Браслет
300 грн.
.35
1,2
Намисто
200₴
.15
.75
Сережки
100 грн.
0,05
.5










