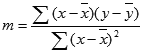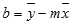LINEST (функція LINEST)

Опис

Функція LINEST обчислює статистику для лінії за допомогою методу "найменших квадратів", щоб обчислити пряму лінію, яка найбільше відповідає вашим даним, а потім повертає масив, що описує цю лінію. Можна також поєднати функцію LINEST з іншими функціями, щоб обчислити статистику для інших типів моделей, які є лінійними в невідомих параметрах, у тому числі поліноміальні, логарифмічні, експоненційні та ступеневі ряди. Оскільки ця функція повертає масив значень, її потрібно вводити як формулу масиву. Необхідні вказівки наведено у прикладах цієї статті.

Формула для лінії має такий вигляд:

y = mx + b

-або-

y = m1x1 + m2x2 + ... + b

якщо існує кілька діапазонів х-значень, де залежні y-значення — це функція незалежних x-значень. m-значення — це коефіцієнти, які відповідають кожному x-значенню, а b — константа. Зауважте, що y, x і m можуть бути векторами. Масив, який повертає функція LINEST, — {mn;mn-1;...,m1;b}. Функція LINEST також може повертати додаткову статистику регресії.

Синтаксис

LINEST(відомі_значення_y;[відомі_значення_x];[конст];[статистика])

Синтаксис функції LINEST має такі аргументи:

Синтаксис

• Відомі_значення_y.    Обов’язковий аргумент. Набір значень y, вже відомих із рівняння y = mx + b.

  • Якщо масив відомі_значення_y є окремим стовпцем, то кожний стовпець відомі_значення_x інтерпретується як окрема змінна.

  • Якщо масив відомі_значення_y міститься в одному рядку, то кожний рядок відомі_значення_x інтерпретується як окрема змінна.

• Відомі_значення_x.    Необов’язковий аргумент. Сукупність значень x, які можуть бути вже відомі з рівняння y = mx + b.

  • Масив відомі_значення_x може містити один або кілька наборів змінних. Якщо використовується лише одна змінна, відомі_значення_y і відомі_значення_x можуть бути діапазонами будь-якої форми, за умови, що вони мають однакову розмірність. Якщо використовується кілька змінних, відомі_значення_y мають бути вектором (тобто діапазоном із висотою в один рядок і шириною в один стовпець).

  • Якщо відомі_значення_x не задано, вважається, що це буде масив {1;2;3;...}, який має той самий розмір, що й відомі_значення_y.

• Конст.    Необов’язковий аргумент. Логічне значення, яке вказує, чи потрібно, щоб константа b дорівнювала 0.

  • Якщо аргумент конст приймає значення TRUE (істина) або його не вказано, b обчислюється у звичайний спосіб.

  • Якщо аргумент конст приймає значення FALSE (хибність), то b вважається рівним 0, а значення m добираються так, щоб y = mx.

• Статистика.    Необов’язковий аргумент. Логічне значення, яке визначає, чи потрібно повертати додаткову статистику регресії.

  • Якщо аргумент «статистика » має значення TRUE, функція LINEST повертає додаткову статистику регресії; у результаті повертається масив {mn;mn-1,...,m1;b; sen,sen-1,...,se1,seb; r^2,sey; F,df; ssreg,ssresid}.

  • Якщо аргумент статистика приймає значення FALSE (хибність) або цей аргумент не вказано, функція LINEST повертає лише m-коефіцієнти й константу b.

    Додаткова статистика регресії має такий вигляд.

На наведеному нижче рисунку показано порядок повернення статистики додаткової регресії.

Примітки

• Можна описати будь-яку пряму лінію за допомогою нахилу та перетину з віссю y:

  Нахил (m):
  Щоб знайти нахил лінії, часто написаної як m, візьміть дві точки на лінії, (x1,y1) і (x2,y2); нахил дорівнює (y2 - y1)/(x2 - x1).

  Перетин Y (b):
  Y-перетин рядка, часто написаного як b, – це значення y в точці перетину осі Y.

  Формула прямої лінії дорівнює y = mx + b. Вивчивши значення m і b, ви можете обчислити будь-яку точку на рядку, підключивши до неї значення y- або x. Також можна скористатися функцією TREND .

• Якщо є лише одна незалежна x-змінна, можна отримати значення нахилу та перетину з віссю y безпосередньо за допомогою таких формул:

  Нахил:
  =INDEX(LINEST(known_y;known_x);1)

  Перетин Y:
  =INDEX(LINEST(known_y;known_x);2)

• Точність апроксимації за допомогою прямої, обчисленої функцією LINEST, залежить від степеня розкиду даних. Чим ближчі дані до прямої, тим точніша модель, яка використовується функцією LINEST. Функція LINEST використовує метод найменших квадратів для визначення найкращої апроксимації даних. Якщо є лише одна незалежна x-змінна, m і b обчислюються за такими формулами:

  

  

  де x і y – вибіркові середні значення, тобто x = AVERAGE(відомі_значення_x), а y = AVERAGE(відомі_значення_y).

• Лінійні та криві функції LINEST і LOGEST можуть обчислити найкращу пряму лінію або експоненційну криву, яка відповідає вашим даним. Однак потрібно вирішити, який із двох результатів найкраще підходить для ваших даних. Ви можете обчислити TREND(known_y,known_x) для прямої лінії або GROWTH(known_y, known_x) для експоненційної кривої. Ці функції без аргументу new_x повертають масив значень y, прогнозованих уздовж цієї лінії або кривої на фактичних точках даних. Потім можна порівняти прогнозовані значення з фактичними значеннями. Їх можна створити на діаграмах для візуального порівняння.

• Здійснюючи регресійний аналіз, Excel обчислює для кожної точки квадрат різниці між прогнозованим значенням у та фактичним значенням у. Сума цих квадратів різниць називається залишковою сумою квадратів (ssresid). Потім Excel обчислює загальну суму квадратів (sstotal). Якщо аргумент конст приймає значення TRUE (істина) або цей аргумент не вказано, загальна сума квадратів дорівнюватиме сумі квадратів різниць між фактичними значеннями y та середніми значеннями у. Якщо аргумент конст приймає значення FALSE (хибність), загальна сума квадратів дорівнюватиме сумі квадратів фактичних значень у (без віднімання середнього значення у від кожного окремого значення у). Після цього регресійну суму квадратів (ssreg) можна обчислити таким чином: ssreg=sstotal-ssresid. Чим менша залишкова сума квадратів, порівняно із загальною сумою квадратів, тим більше значення коефіцієнта визначення r², що є показником того, наскільки добре формула, отримана в результаті регресивного аналізу, пояснює зв'язок між змінними. Значення r² дорівнює ssreg/sstotal.

• У деяких випадках один або кілька стовпців X (припустімо, що стовпці Y і X) можуть не мати додаткового передбачливого значення в присутності інших стовпців X. Іншими словами, усунення одного або кількох стовпців X може призвести до не менш точних прогнозованих значень Y. У такому разі ці зайві стовпці X слід пропустити з моделі регресії. Це явище називається "колінеарність", тому що будь-який надлишковий стовпець X може бути виражений як сума кратних не надлишкових стовпців X. Функція LINEST перевіряє колінеарність і видаляє зайві стовпці X із моделі регресії, коли визначає їх. Видалені стовпці X можна розпізнати у виводі LINEST як такі, що містять коефіцієнти 0 на додачу до значень 0 se. Якщо один або кілька стовпців видаляються як зайві, це впливає на df, оскільки df залежить від кількості стовпців X, які фактично використовуються для передбачливих цілей. Докладні відомості про обчислення df див. у прикладі 4. Якщо змінити df, тому що зайві стовпці X видаляються, значення sey і F також впливають. Колінеарність повинна бути відносно рідкісною на практиці. Однак один випадок, коли може виникнути більша ймовірність того, що деякі стовпці X містять лише 0 і 1 значення як індикатори того, чи є суб'єкт в експерименті учасником певної групи або не є учасником певної групи. Якщо аргумент const = TRUE або його не вказано, функція LINEST ефективно вставляє додатковий стовпець X з усіх 1 значень для моделювання перетину. Якщо у вас є стовпець з 1 для кожної теми, якщо чоловічий або 0, якщо ні, і у вас також є стовпець з 1 для кожної теми, якщо жіночий, або 0, якщо ні, цей останній стовпець надлишковий, оскільки записи в ньому можна отримати від віднімання запису в стовпці "чоловічий індикатор" від запису в додатковому стовпці всіх 1 значень, доданих функцією LINEST .

• Для випадків, коли стовпці Х не видаляються з моделі внаслідок колінеарності, значення df обчислюється таким чином: якщо існує k стовпців аргументу відомі_значення_x і аргумент конст має значення TRUE (істина), або цей аргумент не вказано, то df=n-k-1. Якщо аргумент конст має значення FALSE (хибність), то df=n-k. В обох випадках видалення стовпців Х унаслідок колінеарності збільшує значення df на 1.

• Вводячи константу масиву як, наприклад, аргумент відомі_значення_x, слід використовувати крапку з комою для розділення значень, які містяться в одному рядку, та двокрапку — для розділення рядків. Символи-роздільники можуть відрізнятися залежно від регіональних параметрів.

• Зауважте, що y-значення, прогнозовані рівнянням регресії, можуть не бути припустимими, якщо вони перебувають поза межами діапазону y-значень, використаного для визначення рівняння.

• Основний алгоритм, використовуваний у функції LINEST, відрізняється від основного алгоритму, використовуваного у функціях SLOPE і INTERCEPT. Відмінність між цими алгоритмами може призвести до отримання різних результатів, якщо дані є невизначеними і колінеарними. Наприклад, якщо точки даних аргументу відомі_значення_y дорівнюють 0, а точки даних аргументу відомі_значення_x дорівнюють 1:

  • Функція LINEST повертає значення 0. Алгоритм функції LINEST створено, щоб повертати придатні результати для колінеарних даних, і в такому випадку можна знайти принаймні одну відповідь.

  • Функції SLOPE і INTERCEPT повертають #DIV/0! помилку #REF!. Алгоритм функцій SLOPE і INTERCEPT призначений для пошуку лише однієї відповіді, і в цьому випадку може бути кілька відповідей.

• Крім того, що функцію LOGEST можна використати для обчислення статистики для інших типів регресії, функцію LINEST можна використати для обчислення діапазону інших типів регресії за допомогою введення функцій змінних x та y як рядів x та y для функції LINEST. Наприклад, така формула:

  =LINEST(y-значення; x-значення^COLUMN($A:$C))

  працює, якщо є окремий стовпець y-значень і окремий стовпець x-значень для обчислення кубічного (поліноміального 3-го порядку) наближення форми:

  y = m1*x + m2*x^2 + m3*x^3 + b

  Цю формулу можна змінити для обчислення інших типів регресії, але в деяких випадках буде потрібно змінити результати та іншу статистику.

• Значення F-test, яке повертає функція LINEST, відрізняється від значення F-test, яке повертає функція FTEST1. LINEST повертає статистику F, у той час як FTEST1 повертає ймовірність.

Приклади