Bài viết này được chuyển thể từ Phân tích Dữ liệu Excel và Lập mô hình Kinh doanh của Wayne L. Winston.
-
Ai sử dụng mô phỏng Monte Carlo?
-
Điều gì xảy ra khi bạn nhập =RAND() vào một ô?
-
Làm thế nào bạn có thể mô phỏng các giá trị của một biến ngẫu nhiên riêng?
-
Làm thế nào bạn có thể mô phỏng các giá trị của một biến ngẫu nhiên bình thường?
-
Làm thế nào một công ty thiệp chúc mừng có thể xác định số lượng thiệp để sản xuất?
Chúng tôi muốn ước tính chính xác xác xác suất của các sự kiện không chắc chắn. Ví dụ, xác suất dòng tiền của một sản phẩm mới sẽ có giá trị hiện tại ròng dương (giá trị ròng NPV) là gì? Yếu tố rủi ro của danh mục đầu tư của chúng tôi là gì? Mô phỏng Monte Carlo cho phép chúng tôi mô hình các tình huống mà hiện nay không chắc chắn và sau đó chơi chúng ra trên một máy tính hàng ngàn lần.
Lưu ý: Tên mô phỏng Monte Carlo bắt nguồn từ các mô phỏng máy tính được thực hiện trong những năm 1930 và 1940 để ước tính xác suất rằng phản ứng dây chuyền cần thiết cho một quả bom nguyên tử để phát nổ sẽ hoạt động thành công. Các nhà vật lý tham gia vào tác phẩm này là những người hâm mộ cờ bạc lớn, vì vậy họ đã cung cấp các mô phỏng tên mã Monte Carlo.
Trong năm chương tiếp theo, bạn sẽ thấy các ví dụ về cách bạn có thể sử dụng Excel để thực hiện mô phỏng Monte Carlo.
Nhiều công ty sử dụng mô phỏng Monte Carlo như là một phần quan trọng của quá trình ra quyết định của họ. Dưới đây là một số ví dụ.
-
General Motors, Proctor và Gamble, Pfizer, Bristol-Myers Squibb, và Eli Lilly sử dụng mô phỏng để ước tính cả tỷ suất sinh lợi trung bình và hệ số rủi ro của sản phẩm mới. Tại GM, thông tin này được Tổng Giám đốc sử dụng để xác định sản phẩm nào ra thị trường.
-
GM sử dụng mô phỏng cho các hoạt động như dự báo thu nhập ròng cho công ty, dự đoán chi phí cơ cấu và mua hàng, và xác định mức độ nhạy cảm của nó với các loại rủi ro khác nhau (chẳng hạn như thay đổi lãi suất và biến động tỷ giá hối đoái).
-
Lilly sử dụng mô phỏng để xác định công suất thực vật tối ưu cho từng loại thuốc.
-
Proctor và Gamble sử dụng mô phỏng để mô hình hóa và tối ưu rủi ro giao dịch nước ngoài.
-
Sears sử dụng mô phỏng để xác định số lượng đơn vị của mỗi dòng sản phẩm nên được đặt hàng từ các nhà cung cấp - ví dụ, số lượng các cặp quần Dockers nên được đặt hàng trong năm nay.
-
Các công ty dầu và thuốc sử dụng mô phỏng để định giá "các lựa chọn thực", chẳng hạn như giá trị của một lựa chọn để mở rộng, ký kết hợp đồng hoặc trì hoãn một dự án.
-
Các nhà lập kế hoạch tài chính sử dụng mô phỏng Monte Carlo để xác định các chiến lược đầu tư tối ưu cho quỹ hưu trí của khách hàng.
Khi bạn nhập công thức =RAND() vào một ô, bạn nhận được một số có khả năng bằng nhau giả định bất kỳ giá trị nào từ 0 đến 1. Vì vậy, khoảng 25 phần trăm thời gian, bạn nên có được một số ít hơn hoặc bằng 0,25; khoảng 10 phần trăm thời gian bạn sẽ nhận được một số ít nhất là 0,90, và như vậy. Để minh họa cách hoạt động của hàm RAND, hãy xem tệp được Randdemo.xlsx, hiển thị trong Hình 60-1.
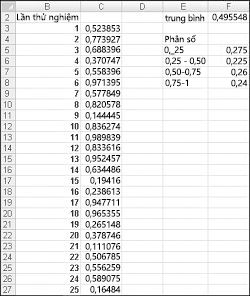
Lưu ý: Khi bạn mở tệp, bạn sẽ Randdemo.xlsx không nhìn thấy các số ngẫu nhiên giống như hiển thị trong Hình 60-1. Hàm RAND luôn tự động tính toán lại các số mà hàm đó tạo ra khi mở một trang tính hoặc khi nhập thông tin mới vào trang tính.
Trước tiên, hãy sao chép từ ô C3 sang Ô C4:C402 công thức =RAND(). Sau đó, bạn đặt tên cho dải ô C3:C402 Dữ liệu. Sau đó, trong cột F, bạn có thể theo dõi trung bình của 400 số ngẫu nhiên (ô F2) và dùng hàm COUNTIF để xác định các phân số nằm trong khoảng từ 0 đến 0,25, 0,25 và 0,50, 0,50 và 0,75 và 0,75 và 1. Khi bạn nhấn phím F9, các số ngẫu nhiên sẽ được tính toán lại. Lưu ý rằng trung bình của 400 số luôn xấp xỉ 0,5 và khoảng 25% kết quả nằm trong khoảng 0,25. Các kết quả này phù hợp với định nghĩa của một số ngẫu nhiên. Ngoài ra, hãy lưu ý rằng các giá trị do RAND tạo ra trong các ô khác nhau là độc lập. Ví dụ, nếu số ngẫu nhiên được tạo ra trong ô C3 là một số lớn (ví dụ: 0,99), nó cho chúng ta biết không có gì về giá trị của các số ngẫu nhiên khác được tạo ra.
Giả sử nhu cầu đối với lịch chịu sự điều chỉnh của biến ngẫu nhiên cụ thể sau đây:
|
Cầu |
Probability |
|---|---|
|
10.000 |
0,10 |
|
20.000 |
0.35 |
|
40,000 |
0,3 |
|
60.000 |
0,25 |
Làm thế nào chúng ta có thể có excel chơi ra, hoặc mô phỏng, nhu cầu này đối với lịch nhiều lần? Bí kíp là liên kết từng giá trị có thể có của hàm RAND với nhu cầu có thể có về lịch. Bài tập sau đảm bảo rằng nhu cầu 10.000 sẽ xảy ra 10 phần trăm thời gian, v.v.
|
Cầu |
Số ngẫu nhiên được gán |
|---|---|
|
10.000 |
Nhỏ hơn 0,10 |
|
20.000 |
Lớn hơn hoặc bằng 0,10 và nhỏ hơn 0,45 |
|
40,000 |
Lớn hơn hoặc bằng 0,45 và nhỏ hơn 0,75 |
|
60.000 |
Lớn hơn hoặc bằng 0,75 |
Để thể hiện mô phỏng nhu cầu, hãy nhìn vào tệp Discretesim.xlsx, hiển thị trong Hình 60-2 trên trang tiếp theo.
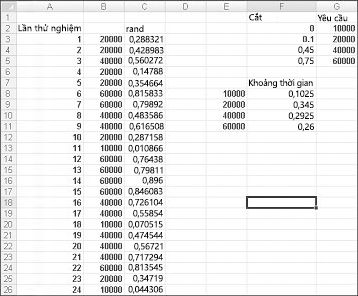
Chìa khóa để mô phỏng của chúng tôi là sử dụng một số ngẫu nhiên để bắt đầu tra cứu từ phạm vi bảng F2:G5 (có tên tra cứu). Các số ngẫu nhiên lớn hơn hoặc bằng 0 và nhỏ hơn 0,10 sẽ cho ra nhu cầu là 10.000; các số ngẫu nhiên lớn hơn hoặc bằng 0,10 và nhỏ hơn 0,45 sẽ tạo ra nhu cầu là 20.000; các số ngẫu nhiên lớn hơn hoặc bằng 0,45 và nhỏ hơn 0,75 sẽ cho ra nhu cầu là 40.000; và các số ngẫu nhiên lớn hơn hoặc bằng 0,75 sẽ cho ra nhu cầu là 60.000. Bạn tạo 400 số ngẫu nhiên bằng cách sao chép từ C3 sang C4:C402 công thức RAND(). Sau đó, bạn tạo 400 phép thử hoặc phép thử cho nhu cầu sử dụng lịch bằng cách sao chép từ B3 đến B4:B402 công thức VLOOKUP(C3,tra cứu,2). Công thức này đảm bảo rằng bất kỳ số ngẫu nhiên nào nhỏ hơn 0,10 tạo ra nhu cầu là 10.000, bất kỳ số ngẫu nhiên nào từ 0,10 đến 0,45 sẽ tạo ra nhu cầu là 20.000, v.v. Trong phạm vi ô F8:F11, hãy sử dụng hàm COUNTIF để xác định phân số của 400 lần thử tạo ra mỗi nhu cầu. Khi chúng ta nhấn F9 để tính toán lại các số ngẫu nhiên, xác suất mô phỏng gần với xác suất yêu cầu giả định của chúng ta.
Nếu bạn nhập vào ô bất kỳ công thức NORMINV(rand(),mu,sigma), bạn sẽ tạo ra giá trị mô phỏng của biến ngẫu nhiên bình thường có giá trị mu trung bình và độ lệch chuẩn sigma. Quy trình này được minh họa trong hình ảnh tệp được Normalsim.xlsx trong Hình 60-3.
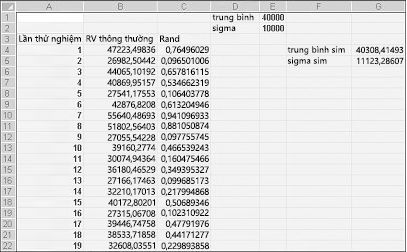
Giả sử chúng ta muốn mô phỏng 400 phép thử hoặc lần thử, cho một biến ngẫu nhiên bình thường với giá trị trung bình là 40.000 và độ lệch chuẩn là 10.000. (Bạn có thể nhập các giá trị này vào các ô E1 và E2 và đặt tên tương ứng cho các ô này là trung bình và sigma.) Sao chép công thức =RAND() từ C4 đến C5:C403 sẽ tạo ra 400 số ngẫu nhiên khác nhau. Sao chép từ B4 sang B5:B403 công thức NORMINV(C4,mean,sigma) tạo ra 400 giá trị thử nghiệm khác nhau từ một biến ngẫu nhiên bình thường với giá trị trung bình là 40.000 và độ lệch chuẩn là 10.000. Khi chúng ta nhấn phím F9 để tính toán lại các số ngẫu nhiên, giá trị trung bình vẫn gần 40.000 và độ lệch chuẩn gần bằng 10.000.
Về cơ bản, đối với một số ngẫu nhiên x, công thức NORMINV(p,mu,sigma) tạo phân vị thứ pcủa một biến ngẫu nhiên bình thường với một mu trung bình và một sigma độ lệch chuẩn. Ví dụ, số ngẫu nhiên 0,77 trong ô C4 (xem Hình 60-3) tạo ra trong ô B4 xấp xỉ phân vị thứ 77 của biến ngẫu nhiên bình thường với trung bình là 40.000 và độ lệch chuẩn là 10.000.
Trong phần này, bạn sẽ thấy làm thế nào mô phỏng Monte Carlo có thể được sử dụng như một công cụ ra quyết định. Giả sử nhu cầu về thẻ Ngày Valentine chịu sự điều chỉnh của biến ngẫu nhiên cụ thể sau đây:
|
Cầu |
Probability |
|---|---|
|
10.000 |
0,10 |
|
20.000 |
0.35 |
|
40,000 |
0,3 |
|
60.000 |
0,25 |
Thiệp chúc mừng được bán với giá $4,00 và chi phí biến đổi để sản xuất mỗi thẻ là $1,50. Thẻ còn lại phải được dùng một lần với chi phí $0,20 cho mỗi thẻ. Bao nhiêu thẻ nên được in?
Về cơ bản, chúng tôi mô phỏng mỗi số lượng sản xuất có thể (10.000, 20.000, 40.000, hoặc 60.000) nhiều lần (ví dụ, 1000 lần lặp). Sau đó, chúng tôi xác định số lượng đơn hàng tạo ra lợi nhuận trung bình tối đa trên 1000 lần lặp. Bạn có thể tìm thấy dữ liệu cho mục này trong tệp được Valentine.xlsx trong Hình 60-4. Bạn gán tên phạm vi trong các ô B1:B11 cho các ô C1:C11. Phạm vi ô G3:H6 được gán tra cứu tên. Giá bán của chúng tôi và các thông số chi phí được nhập vào các ô C4:C6.
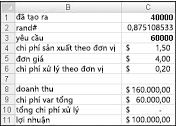
Bạn có thể nhập số lượng sản phẩm dùng thử (40.000 trong ví dụ này) vào ô C1. Tiếp theo, tạo một số ngẫu nhiên trong ô C2 với công thức =RAND(). Như đã mô tả trước đó, bạn mô phỏng nhu cầu về thẻ trong ô C3 với công thức VLOOKUP(rand,lookup,2). (Trong công thức VLOOKUP, rand là tên ô được gán cho ô C3, không phải hàm RAND.)
Số lượng các đơn vị bán được là nhỏ hơn trong số lượng sản xuất và nhu cầu của chúng tôi. Trong ô C8, bạn tính doanh thu của chúng tôi bằng công thức MIN(produced,demand)*unit_price. Trong ô C9, bạn tính toán tổng chi phí sản xuất với công thức được tạo*unit_prod_cost.
Nếu chúng tôi sản xuất nhiều thẻ hơn nhu cầu, số lượng các đơn vị còn lại hơn bằng sản xuất trừ nhu cầu; nếu không thì không còn đơn vị nào. Chúng tôi tính toán chi phí xử lý của mình trong ô C10 bằng công thức unit_disp_cost*IF(được tạo ra>cầu,sản xuất theo yêu cầu,0). Cuối cùng, trong ô C11, chúng tôi tính lợi nhuận dưới dạng doanh thu– total_var_cost-total_disposing_cost.
Chúng tôi muốn một cách hiệu quả để nhấn F9 nhiều lần (ví dụ: 1000) cho mỗi số lượng sản xuất và kiểm tra lợi nhuận dự kiến của chúng tôi cho mỗi số lượng. Tình huống này là một trong đó một bảng dữ liệu hai chiều đến giải cứu của chúng tôi. (Xem Chương 15, "Phân tích Độ nhạy cảm với Bảng Dữ liệu", để biết chi tiết về bảng dữ liệu.) Bảng dữ liệu được sử dụng trong ví dụ này được hiển thị trong Hình 60-5.
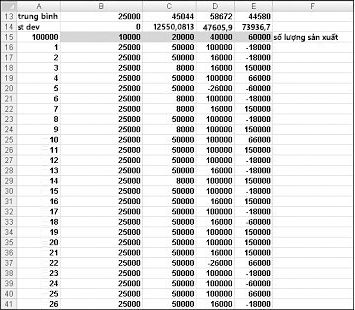
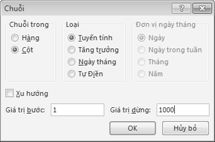
Trong phạm vi ô A16:A1015, nhập các số 1–1000 (tương ứng với 1000 phép thử của chúng tôi). Một cách dễ dàng để tạo các giá trị này là bắt đầu bằng cách nhập 1 vào ô A16. Chọn ô, rồi trên tab Trang đầu trong nhóm Sửa, bấm Vào, rồi chọn Chuỗi để hiển thị hộp thoại Chuỗi. Trong hộp thoại Chuỗi , hiển thị trong Hình 60-6, nhập Giá trị Bước 1 và Giá trị Dừng là 1000. Trong vùng Chuỗi Trong , chọn tùy chọn Cột , rồi bấm OK. Các số 1–1000 sẽ được nhập vào cột A bắt đầu từ ô A16.
Tiếp theo, chúng tôi nhập số lượng sản xuất khả thi của chúng tôi (10.000, 20.000, 40.000, 60.000) trong các ô B15:E15. Chúng tôi muốn tính lợi nhuận cho mỗi số dùng thử (từ 1 đến 1000) và mỗi số lượng sản xuất. Chúng tôi tham chiếu đến công thức lợi nhuận (được tính toán trong ô C11) ở ô phía trên bên trái của bảng dữ liệu (A15) bằng cách nhập =C11.
Chúng tôi hiện đã sẵn sàng để lừa Excel mô phỏng 1000 lần thử nhu cầu cho mỗi số lượng sản xuất. Chọn phạm vi bảng (A15:E1014), rồi trong nhóm Công cụ Dữ liệu trên tab Dữ liệu, bấm Phân tích What If, rồi chọn Bảng Dữ liệu. Để thiết lập bảng dữ liệu hai chiều, hãy chọn số lượng sản xuất (ô C1) làm Ô Nhập Hàng và chọn ô trống bất kỳ (chúng tôi đã chọn ô I14) làm Ô Đầu vào Cột. Sau khi bấm vào OK, Excel sẽ mô phỏng các giá trị nhu cầu 1000 cho mỗi số lượng đơn hàng.
Để hiểu rõ lý do tại sao cách này hoạt động, hãy xem xét các giá trị được đặt bởi bảng dữ liệu trong phạm vi ô C16:C1015. Đối với mỗi ô trong số này, Excel sẽ sử dụng giá trị 20.000 trong ô C1. Trong C16, giá trị ô nhập cột 1 được đặt trong một ô trống và số ngẫu nhiên trong ô C2 sẽ tính toán lại. Lợi nhuận tương ứng sau đó được ghi vào ô C16. Sau đó, giá trị đầu vào của ô cột là 2 được đặt trong một ô trống và số ngẫu nhiên trong C2 sẽ tính toán lại. Lợi nhuận tương ứng được nhập vào ô C17.
Bằng cách sao chép từ ô B13 sang C13:E13 công thức AVERAGE(B16:B1015), chúng tôi tính lợi nhuận mô phỏng trung bình cho mỗi số lượng sản xuất. Bằng cách sao chép từ ô B14 sang C14:E14 công thức STDEV(B16:B1015), chúng tôi tính độ lệch chuẩn của lợi nhuận mô phỏng cho mỗi số lượng đơn hàng. Mỗi lần chúng tôi nhấn F9, 1000 lần thử yêu cầu được mô phỏng cho mỗi số lượng đơn hàng. Sản xuất 40.000 thẻ luôn mang lại lợi nhuận dự kiến lớn nhất. Do đó, dường như việc tạo ra 40.000 lá bài là quyết định đúng đắn.
Tác động của rủi ro trên quyết định của chúng tôi Nếu chúng tôi sản xuất 20.000 thay vì 40.000 thẻ, lợi nhuận dự kiến của chúng tôi giảm khoảng 22 phần trăm, nhưng rủi ro của chúng tôi (được đo bằng độ lệch chuẩn của lợi nhuận) giảm gần 73 phần trăm. Do đó, nếu chúng ta cực kỳ nghịch đảo với rủi ro, việc tạo ra 20.000 thẻ có thể là quyết định đúng đắn. Tình cờ, sản xuất 10.000 thẻ luôn có một độ lệch chuẩn của 0 thẻ bởi vì nếu chúng tôi sản xuất 10.000 thẻ, chúng tôi sẽ luôn luôn bán tất cả chúng mà không có bất kỳ phần còn lại.
Lưu ý: Trong sổ làm việc này, tùy chọn Tính toán được đặt thành Tự động Ngoại trừ Bảng. (Sử dụng lệnh Tính toán trong nhóm Tính toán trên tab Công thức.) Cài đặt này đảm bảo rằng bảng dữ liệu của chúng tôi sẽ không tính toán lại trừ khi chúng tôi nhấn F9, đây là một ý tưởng hay vì một bảng dữ liệu lớn sẽ làm chậm công việc của bạn nếu nó tính toán lại mỗi khi bạn nhập nội dung nào đó vào trang tính. Lưu ý rằng trong ví dụ này, bất cứ khi nào bạn nhấn F9, lợi nhuận có nghĩa là lợi nhuận sẽ thay đổi. Điều này xảy ra vì mỗi lần bạn nhấn F9, một chuỗi khác nhau gồm 1000 số ngẫu nhiên được sử dụng để tạo ra nhu cầu cho mỗi số lượng đơn hàng.
Khoảng Tin cậy cho Lợi nhuận Trung bình Một câu hỏi tự nhiên để đặt ra trong tình huống này là, vào khoảng thời gian nào chúng ta 95 phần trăm chắc chắn lợi nhuận trung bình đúng sẽ giảm? Khoảng này được gọi là khoảng tin cậy 95 phần trăm của lợi nhuận trung bình. Khoảng tin cậy 95 phần trăm cho trung bình của bất kỳ đầu ra mô phỏng nào được tính bằng công thức sau đây:
Trong ô J11, bạn tính toán giới hạn thấp hơn cho khoảng tin cậy 95 phần trăm trên lợi nhuận trung bình khi tạo 40.000 lịch với công thức D13–1,96*D14/SQRT(1000). Trong ô J12, bạn tính giới hạn trên cho khoảng tin cậy 95 phần trăm của chúng tôi với công thức D13+1,96*D14/SQRT(1000). Những phép tính này được hiển thị trong Hình 60-7.
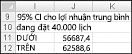
Chúng tôi chắc chắn 95 phần trăm rằng lợi nhuận trung bình của chúng tôi khi 40.000 lịch được đặt hàng trong khoảng $ 56.687 và $ 62.589.
-
Một đại lý GMC tin rằng nhu cầu cho các Đại diện 2005 sẽ được phân phối bình thường với một trung bình của 200 và độ lệch chuẩn 30. Chi phí tiếp nhận một Đại biểu của ông là $ 25,000, và ông bán một Đại biểu với giá $40.000. Một nửa trong số tất cả các Đại biểu không được bán với giá đầy đủ có thể được bán với giá $30.000. Ông đang cân nhắc việc xếp thứ tự 200, 220, 240, 260, 280, hoặc 300 Đại biểu. Ông ta nên ra lệnh bao nhiêu người?
-
Một siêu thị nhỏ đang cố gắng xác định số lượng bản sao của Con người tạp chí họ nên đặt hàng mỗi tuần. Họ tin rằng nhu cầu sử dụng Con người chịu sự điều chỉnh của biến ngẫu nhiên riêng biệt sau đây:
Cầu
Probability
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Siêu thị trả $1,00 cho mỗi bản sao Con người và bán nó với giá $1,95. Mỗi bản sao chưa bán có thể được trả lại với giá $0,50. Đơn hàng của cửa hàng Con người bao nhiêu bản sao?
Bạn cần thêm trợ giúp?
Bạn luôn có thể hỏi chuyên gia trong Cộng đồng kỹ thuật Excel hoặc nhận hỗ trợ trong Cộng đồng.