Sử dụng Bộ giải để lập ngân sách vốn

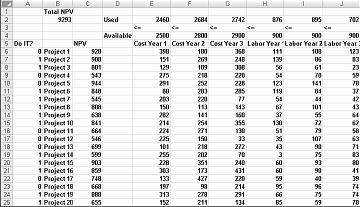
Hầu hết các công ty muốn thực hiện các dự án đóng góp giá trị hiện tại ròng lớn nhất (NPV), phụ thuộc vào các tài nguyên hạn chế (thường là vốn và lao động). Giả sử một công ty phát triển phần mềm đang cố gắng xác định trong số 20 dự án phần mềm sẽ thực hiện. NPV (trị giá hàng triệu đô la) do mỗi dự án đóng góp cũng như vốn (tính bằng triệu đô la) và số lượng lập trình viên cần trong mỗi năm trong ba năm tiếp theo được đưa ra trên trang tính Mô hình Cơ bản trong tệp Capbudget.xlsx, được hiển thị trong Hình 30-1 trên trang tiếp theo. Ví dụ, Project 2 sẽ cho ra kết quả $908 triệu. Tài khoản này yêu cầu $151 triệu trong năm thứ 1, $269 triệu trong năm 2 và $248 triệu trong năm 3. Project 2 yêu cầu 139 lập trình viên trong Năm 1, 86 lập trình viên trong Năm 2 và 83 lập trình viên trong Năm 3. Các ô E4:G4 hiển thị vốn (tính bằng hàng triệu đô la) sẵn có trong mỗi năm trong ba năm và các ô H4:J4 cho biết có bao nhiêu lập trình viên sẵn sàng. Ví dụ, trong Năm 1, có đến $2,5 tỷ vốn và có 900 lập trình viên.

Công ty phải quyết định xem dự án có nên thực hiện từng dự án hay không. Chúng ta hãy giả định rằng chúng ta không thể thực hiện một phần nhỏ của một dự án phần mềm; nếu chúng tôi phân bổ 0,5 tài nguyên cần thiết, ví dụ như chúng tôi sẽ có một chương trình không làm việc có thể mang lại cho chúng tôi doanh thu $0!

Bí quyết để tạo mô hình các tình huống mà bạn làm hoặc không thực hiện điều gì đó là sử dụng ô thay đổi nhị phân. Ô thay đổi nhị phân luôn bằng 0 hoặc 1. Khi một ô thay đổi nhị phân tương ứng với một dự án bằng 1, chúng ta sẽ thực hiện dự án đó. Nếu ô thay đổi nhị phân tương ứng với một dự án bằng 0, thì chúng ta không thực hiện dự án đó. Bạn thiết lập Bộ giải để sử dụng phạm vi ô thay đổi nhị phân bằng cách thêm ràng buộc—hãy chọn những ô thay đổi bạn muốn sử dụng, rồi chọn Bin từ danh sách trong hộp thoại Thêm Ràng buộc.

Với nền tảng này, chúng tôi đã sẵn sàng để giải quyết vấn đề lựa chọn dự án phần mềm. Như thường làm với mô hình Trình giải quyết, chúng ta bắt đầu bằng cách nhận dạng ô đích, ô thay đổi và ràng buộc.

• Ô Đích. Chúng tôi tối đa hóa NPV được tạo bởi các dự án được chọn.

• Thay đổi ô. Chúng ta tìm kiếm ô thay đổi nhị phân 0 hoặc 1 cho mỗi dự án. Tôi đã định vị những ô này trong phạm vi A6:A25 (và được đặt tên là phạm vi doit). Ví dụ: số 1 trong ô A6 cho biết chúng tôi sẽ Project 1; số 0 trong ô C6 cho biết rằng chúng tôi không thực hiện Project 1.

• Các ràng buộc. Chúng tôi cần đảm bảo rằng với mỗi năm t (t=1, 2, 3), vốn t Year được sử dụng nhỏ hơn hoặc bằng chữ hoa năm t có sẵn, và năm t labor được sử dụng sẽ nhỏ hơn hoặc bằng năm t labor sẵn dùng.

Như bạn có thể thấy, trang tính của chúng tôi phải tính toán bất kỳ lựa chọn nào của các dự án NPV, vốn được sử dụng hàng năm và các lập trình viên sử dụng hàng năm. Trong ô B2, tôi sử dụng công thức SUMPRODUCT(doit,NPV) để tính tổng NPV do các dự án được chọn tạo. (Tên phạm vi NPV tham chiếu đến phạm vi C6:C25.) Với mỗi dự án có cột A là 1, công thức này nhận NPV của dự án và đối với mỗi dự án có cột A bằng 0, công thức này không nhận NPV của dự án. Do đó, chúng ta có thể tính NPV của tất cả các dự án, và ô đích của chúng ta là tuyến tính vì nó được tính toán bằng cách tính tổng các thuật ngữ theo sau biểu mẫu (thay đổi ô )*(hằng số). Theo cách tương tự, tôi tính toán chữ hoa được dùng mỗi năm và công thức sử dụng mỗi năm bằng cách sao chép từ E2 đến F2:J2 công thức SUMPRODUCT(doit,E6:E25).

Bây giờ tôi sẽ điền vào hộp thoại Tham số Bộ giải như hiển thị trong Hình 30-2.

Mục tiêu của chúng tôi là tối đa hóa NPV của các dự án đã chọn (ô B2). Các ô thay đổi của chúng tôi (phạm vi có tên là doit) là các ô thay đổi nhị phân cho mỗi dự án. The constraint E2:J2<=E4:J4 ensures that during each year the capital and labor used are less than or equal to the capital and labor available. Để thêm ràng buộc làm cho ô thay đổi trở thành nhị phân, tôi bấm Thêm trong hộp thoại Tham số Bộ giải rồi chọn Bin từ danh sách ở giữa hộp thoại. Hộp thoại Thêm Ràng buộc sẽ xuất hiện như hiển thị trong Hình 30-3.

Mô hình của chúng tôi là tuyến tính vì ô đích được tính toán dưới dạng tổng các thuật ngữ có biểu mẫu (thay đổi ô )*(hằng số) và vì giới hạn sử dụng tài nguyên được tính bằng cách so sánh tổng (ô thay đổi )*( hằng số) với một hằng số.

Với hộp thoại Tham số Bộ giải được điền vào, hãy bấm Giải quyết và chúng ta có kết quả hiển thị trước đó trong Hình 30-1. Công ty có thể có được NPV tối đa $9,293 triệu ($9,293 tỷ) bằng cách chọn Projects 2, 3, 6–10, 14–16, 19 và 20.

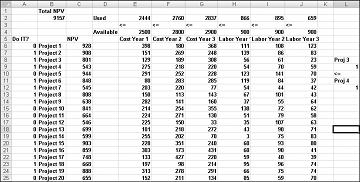
Đôi khi, các mô hình lựa chọn dự án có những ràng buộc khác. Ví dụ: giả sử nếu chúng ta chọn Project 3, chúng ta cũng phải chọn Project 4. Vì giải pháp tối ưu hiện tại của chúng tôi chọn Project 3 nhưng không phải là Project 4, chúng tôi biết rằng giải pháp hiện tại không thể tối ưu. Để giải quyết vấn đề này, chỉ cần thêm ràng buộc rằng ô thay đổi nhị phân cho Project 3 nhỏ hơn hoặc bằng ô thay đổi nhị phân cho Project 4.

Bạn có thể tìm thấy ví dụ này trên trang tính If 3 đến 4 trong tệp Capbudget.xlsx được hiển thị trong Hình 30-4. Ô L9 tham chiếu đến giá trị nhị phân liên quan đến Project 3 và ô L12 tham chiếu đến giá trị nhị phân liên quan Project 4. Bằng cách thêm ràng buộc L9<=L12, nếu chúng ta chọn Project 3, L9 bằng 1 và ràng buộc buộc của chúng ta là L12 (nhị phân Project 4) để bằng 1. Ràng buộc của chúng tôi cũng phải để giá trị nhị phân trong ô thay đổi Project 4 không hạn chế nếu chúng ta không chọn Project 3. Nếu chúng ta không chọn Project 3, thì L9 bằng 0 và ràng buộc của chúng ta cho phép nhị phân Project 4 bằng 0 hoặc 1, đó là điều chúng ta muốn. Giải pháp tối ưu mới được hiển thị trong Hình 30-4.

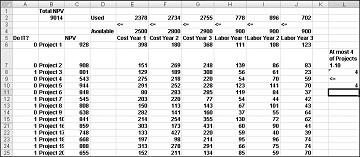
Một giải pháp tối ưu mới được tính toán nếu chọn Project 3 nghĩa là chúng ta cũng phải Project 4. Bây giờ giả sử rằng chúng ta chỉ có thể thực hiện bốn dự án từ 1 đến 10. (Xem trang tính At Most 4/P1-P10 , hiển thị trong Hình 30-5.) Trong ô L8, chúng tôi tính tổng các giá trị nhị phân liên kết với Projects 1 đến 10 bằng công thức SUM(A6:A15). Sau đó, chúng tôi thêm ràng buộc L8<=L10, để đảm bảo rằng, tối đa 4 trong số 10 dự án đầu tiên được chọn. Giải pháp tối ưu mới được hiển thị trong Hình 30-5. NPV đã giảm xuống còn $9,014 tỷ.

Mô hình Bộ giải Tuyến tính, trong đó một số hoặc tất cả các ô thay đổi bắt buộc phải là nhị phân hoặc số nguyên thường khó giải quyết hơn mô hình tuyến tính, trong đó tất cả các ô thay đổi đều được phép là phân số. Vì lý do này, chúng tôi thường hài lòng với giải pháp gần tối ưu cho vấn đề lập trình nhị phân hoặc số nguyên. Nếu mô hình Bộ giải của bạn chạy trong một thời gian dài, bạn có thể muốn xem xét điều chỉnh thiết đặt Dung sai trong hộp thoại Tùy chọn Bộ giải. (Xem Hình 30-6.) Ví dụ: thiết đặt Dung sai của 0,5% nghĩa là Trình giải quyết sẽ dừng lần đầu tiên nó tìm thấy giải pháp khả thi, trong phạm vi 0,5 phần trăm giá trị ô đích tối ưu theo lý thuyết (giá trị ô đích tối ưu theo lý thuyết là giá trị đích tối ưu được tìm thấy khi bỏ qua các giới hạn nhị phân và số nguyên). Thông thường chúng ta sẽ đối mặt với lựa chọn giữa việc tìm câu trả lời trong vòng 10 phần trăm tối ưu trong 10 phút hoặc tìm giải pháp tối ưu trong hai tuần liền với máy tính! Giá trị Dung sai mặc định là 0,05%, có nghĩa là Bộ giải ngừng khi tìm thấy giá trị ô Đích trong phạm vi 0,05 phần trăm giá trị đích tối ưu lý thuyết.

1. Một công ty có chín dự án đang được cân nhắc. NPV đã thêm vào bởi từng dự án và vốn bắt buộc của mỗi dự án trong hai năm tiếp theo được thể hiện trong bảng sau. (Tất cả các số có hàng triệu.) Ví dụ, Project 1 sẽ thêm $14 triệu trong NPV và cần chi phí $12 triệu trong Năm 1 và $3 triệu trong Năm 2. Vào năm 1, vốn $50 triệu có sẵn cho các dự án và $ 20 triệu sẵn dùng trong năm 2.

	NPV	Chi phí năm 1	Chi phí năm 2
Project 1	14	12	3
Project 2	17	54	7
Project 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
Project 6	12	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	12	18	3

• Nếu chúng ta không thể thực hiện phân số của một dự án nhưng phải thực hiện toàn bộ hoặc không thực hiện dự án nào thì chúng ta có thể tối đa hóa NPV bằng cách nào?

• Giả sử nếu Project 4 được thực hiện, bạn Project 5 phải được thực hiện. Làm thế nào để chúng tôi tối đa hóa NPV?

• Một công ty phát hành đang tìm cách xác định xem nên phát hành sách nào trong số 36 sách trong năm nay. Bài viết Pressdata.xlsx cho biết thông tin sau đây về từng cuốn sách:

  • Chi phí phát triển và doanh thu dự kiến (tính bằng hàng nghìn đô-la)

  • Các trang trong mỗi cuốn sách

  • Liệu cuốn sách có hướng đến đối tượng người xem các nhà phát triển phần mềm hay không (được biểu thị bằng số 1 trong cột E)

    Một công ty phát hành có thể phát hành tổng cộng tối đa 8500 trang trong năm nay và phải phát hành ít nhất bốn sách hướng đến các nhà phát triển phần mềm. Làm thế nào để công ty có thể tối đa hóa lợi nhuận của công ty?

Bài viết này được chuyển thể từ Microsoft Office Excel lập mô hình kinh doanh và phân tích dữ liệu năm 2007 của Wayne L. Winston.

Cuốn sách kiểu lớp học này được phát triển từ một loạt các bài trình bày của Wayne Winston, một nhà thống kê và giáo sư kinh doanh nổi tiếng, người đã nghiêng ứng dụng sáng tạo, thực hành của Excel.