本文是從 Microsoft Excel Data Analysis 和 Business Modeling 由 Google L. Winston 所修正。
-
誰使用 Monte Carlo 模擬?
-
當您在儲存格中輸入 =RAND () 時會發生什麼情況?
-
如何模擬離散隨機變數的值?
-
如何模擬一般隨機變數的值?
-
賀卡公司如何決定要產生多少張卡片?
我們想要精確估計不確定事件的機能。 例如,新產品的現金流量有正凈現值 (NPV) 的機率為何? 我們的投資組合的風險因素為何? Monte Carlo 模擬可讓我們模擬呈現不確定狀況,然後在計算機上播放數千次。
附註: Monte Carlo 模擬這個名稱來自於 1930 和 1940s 期間所執行的電腦模擬,以估算一顆原式爆炸所需的鏈結反應成功運作的機率。 參與這項工作的專家是熱想進階的人,因此他們給了模擬程式代碼名稱 Monte Carlo。
在接下來的五章中,您會看到如何使用 Excel 執行 Monte Carlo 仿真的範例。
許多公司都使用 Monte Carlo 模擬做為其決策程式的重要部分。 以下是一些範例。
-
General Motors、Proctor 和,Pfizer、Bristol-Myers Squibb 和 Eli Lilly 使用模擬來估算新產品的平均傳回量和風險係數。 在 GM 中,CEO 會使用此資訊來判斷哪些產品即將上市。
-
GM 會針對模擬活動使用模擬功能,例如預測公司的凈收益、預測結構及購買成本,以及判斷其對於不同類型風險 (的敏感性,例如利率變動和匯率波動) 。
-
Lilly 會使用模擬來判斷每個植物的最佳植物容量。
-
Proctor 和必要工具會使用模擬功能來模型並優化對沖匯率風險。
-
Sears 會使用模擬功能來判斷每個產品線應該向供貨商訂購多少個單位,例如,今年應該訂購的擴充座組數。
-
油品和海洋公司會使用模擬來估值「實際選項」,例如展開、合約或延後項目的選項值。
-
財務規劃者使用 Monte Carlo 模擬來決定客戶淘汰時的最佳投資策略。
當您在儲存格中輸入公式 =RAND () 時,您會得到一個同樣可能假設 0 到 1 之間的任何值的數位。 因此,大約 25% 的時間,您應該會得到小於或等於 0.25 的數位;大約 10% 的時間應取得至少 0.90 的數位,依此類作。 若要示範 RAND 函數的運作方式,請查看檔案 Randdemo.xlsx,如圖 60-1 所示。
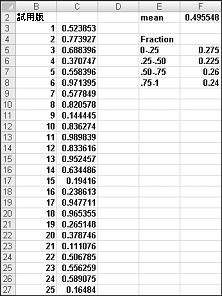
附註: 當您開啟檔案 Randdemo.xlsx 時,您不會看到圖 60-1 中顯示的隨機數。 RAND 函數一律會在工作表開啟或輸入新資訊至工作表時,自動重新計算所產生的數位。
首先,從儲存格 C3 複製到 C4:C402 公式 =RAND () 。 然後,您將範圍命名為 C3:C402 數據。 然後,在欄 F 中,您可以追蹤單元格 F2 (400 隨機數的平均值) ,並使用 COUNTIF 函數來判斷介於 0 到 0.25、0.25 和 0.50、0.50 和 0.75 之間的分數,以及 0.75 和 1。 當您按 F9 鍵時,會重新計算隨機數位。 請注意,400 個數位的平均值一律大約是 0.5,而結果的 25% 左右是以 0.25 為間隔。 這些結果與隨機數的定義一致。 同時請注意,RAND 在不同儲存格中產生的值是獨立的。 例如,如果儲存格 C3 中產生的隨機數是大型數位 (例如 0.99) ,則不會告訴我們其他所產生的隨機數值。
假設行事曆的需求受到下列離散隨機變數的規範:
|
需求 |
[可能性] |
|---|---|
|
10,000 |
0.10 |
|
20,000 |
0.35 |
|
40,000 |
0.3 |
|
60,000 |
0.25 |
我們如何讓 Excel 播放或模擬這個行事曆需求多次? 訣竅在於將 RAND 函數的每個可能值與行事曆的可能需求建立關聯。 下列作業可確保 10,000 的需求會在 10% 的時間出現,依此類作。
|
需求 |
已指派隨機數 |
|---|---|
|
10,000 |
小於 0.10 |
|
20,000 |
大於或等於 0.10,且小於 0.45 |
|
40,000 |
大於或等於 0.45,且小於 0.75 |
|
60,000 |
大於或等於0.75 |
若要示範仿真的需求,請查看檔案 Discretesim.xlsx,如下一頁的圖 60-2 所示。
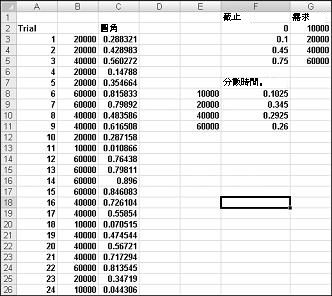
仿真的關鍵在於使用隨機數 從名為查 閱) 的表格範圍 F2:G5 (起始查閱。 大於或等於 0 且小於 0.10 的隨機數會產生 10,000 的需求;大於或等於 0.10 且小於 0.45 的隨機數會產生 20,000 的需求;大於或等於 0.45 且小於 0.75 的隨機數會產生 40,000 的需求;而大於或等於 0.75 的隨機數會產生 60,000 的需求。 從 C3 複製到 C4:C402 公式 RAND () ,即可產生 400 個隨機數。 接著,從 B3 複製到 B4:B402 公式 VLOOKUP (C3、lookup、2 ) ,即可產生 400 個行事歷需求的試用或反覆運算。 此公式可確保任何小於 0.10 的隨機數產生 10,000 的需求,任何介於 0.10 到 0.45 之間的隨機數會產生 20,000,依此類別。 在 F8:F11 單元格範圍中,使用 COUNTIF 函數來判斷 400 次反覆運算中每個需求的分數。 當我們按 F9 以重新計算隨機數時,仿真的機碼會接近我們的假設需求前導參照。
如果您在公式 NORMINV (rand () 、mu、sigma) 的任何單元格中輸入,您將會產生一般隨機變數的模擬值,其中包含平均靜音和標準偏差移轉移轉。 此程式會在檔案 Normalsim.xlsx 中說明,顯示在圖 60-3 中。
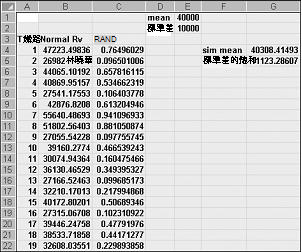
假設我們想要針對平均值為 40,000 且標準偏差為 10,000 的一般隨機變數模擬 400 次試用或反覆運算。 (您可以在儲存格 E1 和 E2 中輸入這些值,並分別命名這些儲存格 平均 值和 sigma。) 將公式 =RAND () 從 C4 複製到 C5:C403 會產生 400 個不同的隨機數。 將公式從 B4 複製到 B5:B403 NORMINV (C4,mean,sigma) 從一般隨機變數產生 400 個不同的試用值,平均值為 40,000 且標準偏差為 10,000。 當我們按 F9 鍵以重新計算隨機數位時,平均值會維持接近 40,000,標準偏差接近 10,000。
基本上,如果是隨機數 x,公式 NORMINV (p,mu,sigma) 產生一般隨機變數的第 p個百分位數,其中包含平均靜音和標準偏差 sigma。 例如,單元格 C4 中的隨機數 0.77 (參閱圖 60-3) 在單元格 B4 中產生,大約是一般隨機變數的第 77 個百分位數,平均值為 40,000,標準偏差為 10,000。
本節將說明如何使用 Monte Carlo 模擬做為決策工具。 假設情人節卡片的需求受到下列隨機變數控制:
|
需求 |
[可能性] |
|---|---|
|
10,000 |
0.10 |
|
20,000 |
0.35 |
|
40,000 |
0.3 |
|
60,000 |
0.25 |
賀卡的售價為 $4.00,而產生每張卡片的變動成本為 $1.50。 左側卡片必須以每張卡 $0.20 的價格丟棄。 應該列印多少張卡片?
基本上,我們 (10,000、20,000、40,000 或 60,000) ,多次模擬每個可能 (的生產數量,例如 1000 次反覆運算) 。 然後,我們決定哪一個訂單數量能得出超過 1000 次反覆運算的最大平均利潤。 您可以在檔案 Valentine.xlsx 中找到此區段的數據,如圖 60-4 所示。 您將儲存格 B1:B11 中的範圍名稱指派給儲存格 C1:C11。 單元格範圍 G3:H6 會指派名稱 查閱。 我們的銷售價格和成本參數是在儲存格 C4:C6 中輸入。
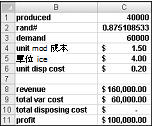
您可以在此範例中輸入試用生產數量 (40,000) 儲存格 C1。 接下來,在儲存格 C2 中建立隨機數,並使用公式 =RAND () 。 如先前所述,您在單元格 C3 中使用公式 VLOOKUP (rand,lookup,2) 模擬卡片需求。 (在 VLOOKUP 公式中, rand 是指派給儲存格 C3 的儲存格名稱,而不是 RAND 函數。)
銷售量是生產數量和需求的較小值。 在儲存格 C8 中,您使用產生的公式 MIN (計算我們的營收 ,要求) *unit_price。 在儲存格 C9 中,您可以使用 產生*unit_prod_cost的公式來計算總生產成本。
如果我們產生的卡片數量超過需求,則超出等於生產減號需求的剩餘數量;否則沒有剩餘的單位。 我們在儲存格 C10 中使用公式 unit_disp_cost*IF (產生>需求、生產需求、0 ) 計算我們的處置成本。 最後,在儲存格 C11 中,我們將利潤計算為 營收,total_var_cost-total_disposing_cost。
我們希望能有效率地按多次 F9 (例如,每個生產量有 1000) ,並計算每個數量的預期利潤。 這種情況下,我們需提供雙向數據表來進行救援。 (請參閱第 15 章的,以取得運算清單的詳細資料。) 此範例中所使用的數據表會顯示在圖 60-5 中。
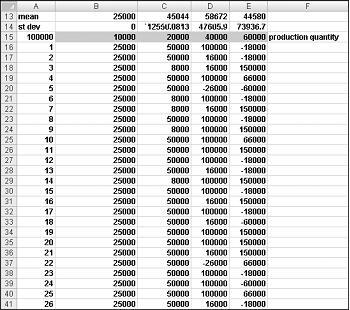
在儲存格範圍 A16:A1015 中,輸入與 1000 次試用) 對應的 1-1000 (數位。 建立這些值的一個簡單方法是在單元格 A16 中輸入 1。 選取單元格,然後在 [常用] 索引標籤的 [編輯] 群組中,按兩下 [填滿],然後選取 [數列] 以顯示 [數列] 對話框。 在 [ 數列 ] 對話框中,顯示在 [圖 60-6] 中,輸入 1 的步驟值和 1000 的停止值。 在 [ 數列內 ] 區域中,選取 [ 欄] 選項,然後按兩下 [ 確定]。 1 到 1000 的數位會從儲存格 A16 開始輸入 A 欄。
接下來,在單元格 B15:E15 中輸入可能的生產數量 (10,000、20,000、40,000、60,000) 。 我們想要計算每個試用版編號 (1 到 1000) 及每個生產量的收益。 我們參照的公式是以儲存格 C11 計算 () 資料表左上儲存格中的公式, (A15) 輸入 =C11。
我們現在已準備好誘騙 Excel 針對每個生產量量進行 1000 次需求反覆運算。 選取 A15:E1014) (數據表範圍,然後在 [數據] 索引標籤的 [資料工具] 群組中,按兩下 [分析時的狀況],然後選取 [數據表]。 若要設定雙向數據表,請選擇我們的生產數量 (單元格 C1) 做為列輸入單元格,然後選取任何空白單元格 (我們選擇儲存格 I14) 做為欄輸入儲存格。 按兩下 [確定] 之後,Excel 會針對每個訂單數量模擬 1000 個需求值。
若要瞭解其運作原因,請考慮數據表在儲存格範圍 C16:C1015 中所放置的值。 針對這些儲存格的每個儲存格,Excel 在儲存格 C1 中會使用 20,000 的值。 在 C16 中,1 的欄輸入儲存格值會放在空白儲存格中,而儲存格 C2 中的隨機數會重新計算。 對應的利潤接著會記錄在儲存格 C16 中。 接著,2 的欄單元格輸入值會放在空白儲存格中,而 C2 中的隨機數會再次重新計算。 對應的利潤會輸入到單元格 C17 中。
從儲存格 B13 複製到 C13:E13 公式 AVERAGE (B16:B1015) ,我們會計算每個生產量的平均模擬利潤。 從單元格 B14 複製到 C14:E14 公式 STDEV (B16:B1015) ,我們會計算每筆訂單數量的模擬利潤標準偏差。 每次我們按 F9 時,每個訂單數量都會模擬 1000 次的需求反覆運算。 產生 40,000 張卡片的收益永遠都是最大的預期利潤。 因此,產生 40,000 張卡片是適當的決定。
風險對我們決策的影響 如果我們生產 20,000 張卡片,而非 40,000 張卡片,預期利潤會降低約 22%,但以利潤標準偏差為單位計算,我們的風險) (會降低近 73%。 因此,如果我們極常規避風險,產生 20,000 張卡片可能是正確決定。 順便說一句,產生 10,000 張卡片一律有 0 張卡片的標準偏差,因為如果我們生產 10,000 張卡片,我們一律會銷售所有卡片,而不會有任何剩下卡。
附註: 在此活頁簿中, [計算] 選項設定 為 [表格除外]。 (使用 [公式] 索引標籤上 [計算] 群組中的 [計算] 命令。) 此設定可確保除非我們按 F9,否則不會重新計算數據表,因為大型數據表會在您每次在工作表中輸入內容時重新計算時變慢。 請注意,在此範例中,每當您按 F9 時,平均利潤就會變更。 這是因為每次按 F9 時,會使用不同順序的 1000 隨機數位來產生每個訂單數量的需求。
平均利潤的信賴區間 在這種情形下,我們自然會問到,我們 95% 的時間間隔確定實際平均利潤會降到什麼時間? 此間隔稱為 平均利潤的95%信賴區間。 任何模擬輸出平均值的 95% 信賴區間是由下列公式計算:
在單元格 J11 中,當公式 D13-1.96*D14/SQRT (1000) 產生 40,000 個行事歷時,您計算平均利潤 95% 信賴區間的下限。 在儲存格 J12 中,您使用公式 D13+1.96*D14/SQRT (1000) 計算 95% 信賴區間的上限。 這些計算會顯示在圖 60-7 中。
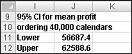
95% 確定訂購 40,000 個行事歷時的平均利潤是 $56,687 到 $62,589。
-
一位 GMC 經銷商認為,2005 年通道的需求通常會以平均值 200 和標準偏差 30 來分配。 他收到「異色」的費用是 $25,000 美元,而他銷售的是 $40,000 美元。 一半未以完整價格販賣的檔案可以賣到 $30,000 美元。 他正在考慮訂購 200、220、240、260、280 或 300 個新功能。 他應該訂購多少個?
-
一位小型的冊子正在嘗試判斷他們每周應該訂購多少份 人員 雜誌。 他們相信他們的 人員 需求受到下列獨立隨機變數所規範:
需求
[可能性]
15
0.10
20
0.20
25
0.30
30
0.25
35
0.15
-
每份 人員 的金額為 $1.00 美元,並以 $1.95 販賣。 每份未售出的複本都可以 $0.50 退還。 商店訂單應該有多少份 人員 份?
需要更多協助嗎?
您可以隨時詢問 Excel 技術社群中的專家,或在社群中取得支援。