単一項の二項分布確率を返します。 BINOMDIST 関数は、テストや試行の回数が固定されている問題で、どの試行の結果も成功または失敗のみで表される場合、各試行が独立している場合、および試行全体をとおして成功の確率が一定である場合に使用します。 たとえば、二男一女が生まれてくる確率などを BINOMDIST で計算できます。
重要: この関数は、より精度が高く、その使い方をより適切に表す名前を持つ、新しい 1 つ以上の関数で置き換えられました。 この関数は下位互換性のために引き続き利用可能ですが、Excel の将来のバージョンでは利用できなくなる可能性があるため、今後は新しい関数を使用することを検討してください。
新しい関数の詳細については、「BINOM.DIST 関数」を参照してください。
書式
BINOMDIST(成功数,試行回数,成功率,関数形式)
BINOMDIST 関数の書式には、次の引数があります。
-
成功数 必ず指定します。 試行における成功数を指定します。
-
試行回数 必ず指定します。 独立試行の回数を指定します。
-
成功率 必ず指定します。 各試行が成功する確率を指定します。
-
関数形式 必ず指定します。 計算に使用する関数の形式を論理値で指定します。 関数形式に TRUE を指定した場合、BINOM.DIST 関数の戻り値は累積分布関数となり、0 ~成功数回の範囲で成功が得られる確率が計算されます。FALSE の場合は、確率質量関数となり、成功数回の成功が得られる確率が計算されます。
解説
-
成功数と試行回数は、整数に切り捨てられます。
-
成功数、試行回数、成功率に数値以外の値を指定すると、エラー値 #VALUE! が返されます。
-
成功数 < 0 または成功数 > 試行回数の場合は、エラー値 #NUM! が返されます。
-
成功率 < 0 または成功率 > 1 の場合は、エラー値 #NUM! が返されます。
-
x = 成功数、n = 試行回数、p = 成功率の場合、二項確率質量関数は次の数式で表されます。
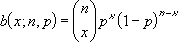
ここで

は COMBIN(n,x) を表します。
-
x = 成功数、n = 試行回数、p = 成功率の場合、累積二項分布は次の数式で表されます。
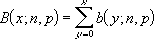
使用例
次の表のサンプル データをコピーし、新しい Excel ワークシートのセル A1 に貼り付けます。 数式を選択して、F2 キーを押し、さらに Enter キーを押すと、結果が表示されます。 必要に応じて、列幅を調整してすべてのデータを表示してください。
|
データ |
説明 |
|
|
6 |
成功数 |
|
|
10 |
試行回数 |
|
|
0.5 |
成功率 |
|
|
数式 |
説明 |
結果 |
|
=BINOMDIST(A2,A3,A4,FALSE) |
10 回の試行のうち、ちょうど 6 回成功する確率を求めます。 |
0.2050781 |










