هام: سينتهي دعم Office 2016 وOffice 2019 في 14 أكتوبر 2025. الترقية إلى Microsoft 365 للعمل في أي مكان من أي جهاز ومتابعة تلقي الدعم. الحصول على Microsoft 365
تتناول هذه المقالة استخدام Solver، وهو برنامج الوظائف الإضافية ل Microsoft Excel الذي يمكنك استخدامه لتحليل ماذا لو، لتحديد مزيج منتج مثالي.
كيف يمكنني تحديد مزيج المنتج الشهري الذي يزيد من الربحية؟
غالبا ما تحتاج الشركات إلى تحديد كمية كل منتج لإنتاجه شهريا. في أبسط شكل، تتضمن مشكلة مزيج المنتج كيفية تحديد كمية كل منتج يجب إنتاجه خلال شهر لتحقيق أقصى قدر من الأرباح. يجب أن يلتزم مزيج المنتج عادة بالقيود التالية:
-
لا يمكن لمزيج المنتجات استخدام موارد أكثر مما هو متاح.
-
هناك طلب محدود على كل منتج. لا يمكننا إنتاج أكثر من منتج خلال شهر مما يفرضه الطلب، لأن الإنتاج الزائد يتم إهداره (على سبيل المثال، دواء قابل للتلف).
لنحل الآن المثال التالي لمشكلة مزيج المنتج. يمكنك العثور على حل لهذه المشكلة في Prodmix.xlsx الملف، الموضح في الشكل 27-1.
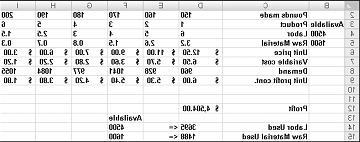
لنفترض أننا نعمل في شركة أدوية تنتج ستة منتجات مختلفة في مصنعها. يتطلب إنتاج كل منتج العمالة والمواد الخام. يظهر الصف الرابع في الشكل 27-1 ساعات العمل اللازمة لإنتاج رطل من كل منتج، ويظهر الصف 5 جنيها من المواد الخام اللازمة لإنتاج رطل من كل منتج. على سبيل المثال، يتطلب إنتاج رطل من المنتج 1 ست ساعات من العمل و3.2 رطل من المواد الخام. لكل دواء، يتم إعطاء سعر الجنيه الواحد في الصف 6، ويتم إعطاء تكلفة الوحدة لكل جنيه في الصف 7، ويتم إعطاء مساهمة الربح للرطل في الصف 9. على سبيل المثال، المنتج 2 يبيع مقابل 11.00 دولار للرطل الواحد، ويتكبد تكلفة وحدة 5.70 دولار للرطل، ويساهم ب 5.30 دولار ربح للرطل. يتم إعطاء طلب الشهر على كل دواء في الصف 8. على سبيل المثال، الطلب على المنتج 3 هو 1041 جنيه. هذا الشهر ، 4500 ساعة من العمل و 1600 جنيه من المواد الخام المتاحة. كيف يمكن لهذه الشركة زيادة أرباحها الشهرية إلى أقصى حد؟
إذا لم نكن نعرف شيئا عن Excel Solver، فسنهاجم هذه المشكلة عن طريق إنشاء ورقة عمل لتتبع الربح واستخدام الموارد المقترنة بمزيج المنتجات. ثم سنستخدم التجربة والخطأ لتغيير مزيج المنتج لتحسين الربح دون استخدام المزيد من العمالة أو المواد الخام مما هو متاح، ودون إنتاج أي دواء يتجاوز الطلب. نستخدم Solver في هذه العملية فقط في مرحلة التجربة والخطأ. بشكل أساسي، Solver هو محرك تحسين يقوم بإجراء البحث التجريبي والخطأ بشكل لا تشوبه شائبة.
أحد المفاتيح لحل مشكلة مزيج المنتج هو حساب استخدام الموارد والأرباح المرتبطة بأي مزيج منتج معين بكفاءة. أداة مهمة يمكننا استخدامها لإجراء هذا الحساب هي الدالة SUMPRODUCT. تقوم الدالة SUMPRODUCT بضرب القيم المقابلة في نطاقات الخلايا وإرجاع مجموع تلك القيم. يجب أن يكون لكل نطاق خلايا مستخدم في تقييم SUMPRODUCT نفس الأبعاد، مما يعني أنه يمكنك استخدام SUMPRODUCT مع صفين أو عمودين، ولكن ليس بعمود واحد وصف واحد.
كمثال على كيفية استخدام وظيفة SUMPRODUCT في مثال مزيج المنتجات لدينا، دعونا نحاول حساب استخدام الموارد لدينا. يتم حساب استخدامنا للعمالة من خلال
(العمالة المستخدمة لكل رطل من المخدرات 1)*(المخدرات 1 جنيه تنتج)+ (العمالة المستخدمة لكل رطل من المخدرات 2)*(المخدرات 2 جنيه تنتج) + ... (العمالة المستخدمة لكل رطل من المخدرات 6)*(المخدرات 6 جنيه تنتج)
يمكننا حساب استخدام العمالة بطريقة أكثر مملة مثل D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. وبالمثل، يمكن حساب استخدام المواد الخام ك D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. ومع ذلك، فإن إدخال هذه الصيغ في ورقة عمل لستة منتجات يستغرق وقتا طويلا. تخيل كم من الوقت سيستغرق الأمر إذا كنت تعمل مع شركة تنتج، على سبيل المثال، 50 منتجا في مصنعهم. هناك طريقة أسهل بكثير لحساب العمالة واستخدام المواد الخام وهي نسخ الصيغة من D14 إلى D15 SUMPRODUCT ($D$2:$I$2,D4:I4). تحسب هذه الصيغة D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (وهو استخدام العمالة لدينا) ولكن من الأسهل بكثير إدخاله! لاحظ أنني أستخدم علامة $ مع النطاق D2:I2 بحيث عند نسخ الصيغة ما زلت ألتقط مزيج المنتج من الصف 2. تحسب الصيغة في الخلية D15 استخدام المواد الخام.
بطريقة مماثلة، يتم تحديد أرباحنا من خلال
(المخدرات 1 الربح لكل جنيه)*(المخدرات 1 جنيه المنتجة) + (المخدرات 2 الربح لكل جنيه)*(المخدرات 2 جنيه المنتجة) + ... (المخدرات 6 الربح لكل جنيه)*(المخدرات 6 جنيه المنتجة)
يتم حساب الربح بسهولة في الخلية D12 باستخدام الصيغة SUMPRODUCT(D9:I9,$D$2:$I$2).
يمكننا الآن تحديد المكونات الثلاثة لنموذج Solver لمزيج منتجاتنا.
-
الخلية الهدف. هدفنا هو زيادة الربح (المحسوبة في الخلية D12).
-
تغيير الخلايا. عدد الرطلات المنتجة لكل منتج (مدرج في نطاق الخلايا D2:I2)
-
القيود. لدينا القيود التالية:
-
لا تستخدم عمالة أو مواد خام أكثر مما هو متاح. أي أن القيم الموجودة في الخلايا D14:D15 (الموارد المستخدمة) يجب أن تكون أقل من القيم الموجودة في الخلايا F14:F15 أو مساوية لها (الموارد المتوفرة).
-
لا تنتج أكثر من المخدرات مما هو عليه في الطلب. أي أن القيم الموجودة في الخلايا D2:I2 (الرطل المنتج لكل دواء) يجب أن تكون أقل من أو تساوي الطلب على كل دواء (مدرج في الخلايا D8:I8).
-
لا يمكننا إنتاج كمية سالبة من أي دواء.
-
سأوضح لك كيفية إدخال الخلية الهدف وتغيير الخلايا والقيود في Solver. ثم كل ما عليك القيام به هو النقر فوق الزر حل للعثور على مزيج منتج تعظيم الربح!
للبدء، انقر فوق علامة التبويب بيانات، وفي المجموعة تحليل، انقر فوق Solver.
ملاحظة: كما هو موضح في الفصل 26، "مقدمة للتحسين باستخدام Excel Solver"، يتم تثبيت Solver بالنقر فوق زر Microsoft Office، ثم خيارات Excel، متبوعة ب الوظائف الإضافية. في القائمة إدارة، انقر فوق وظائف Excel الإضافية، وحدد المربع الوظيفة الإضافية Solver، ثم انقر فوق موافق.
سيظهر مربع الحوار معلمات Solver، كما هو موضح في الشكل 27-2.
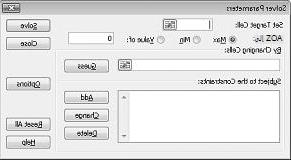
انقر فوق المربع تعيين الخلية الهدف ثم حدد خلية الربح (الخلية D12). انقر فوق المربع By Changing Cells ثم أشر إلى النطاق D2:I2، الذي يحتوي على الجنيهات المنتجة لكل دواء. يجب أن يبدو مربع الحوار الآن الشكل 27-3.
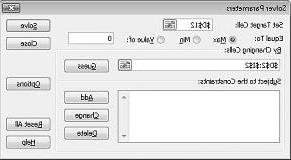
نحن الآن جاهزون لإضافة قيود إلى النموذج. انقر فوق الزر إضافة. سترى مربع الحوار إضافة قيد، الموضح في الشكل 27-4.
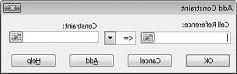
لإضافة قيود استخدام الموارد، انقر فوق المربع مرجع الخلية، ثم حدد النطاق D14:D15. حدد <= من القائمة الوسطى. انقر فوق المربع قيد، ثم حدد نطاق الخلية F14:F15. يجب أن يبدو مربع الحوار إضافة قيد الآن مثل الشكل 27-5.
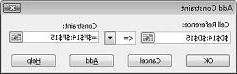
لقد تأكدنا الآن من أنه عندما يحاول Solver قيما مختلفة للخلايا المتغيرة، سيتم النظر فقط في التركيبات التي تلبي كل من D14<=F14 (العمالة المستخدمة أقل من العمالة المتاحة أو مساوية لها) وD15<=F15 (المواد الخام المستخدمة أقل من أو تساوي المواد الخام المتاحة). انقر فوق إضافة لإدخال قيود الطلب. املأ مربع الحوار إضافة قيد كما هو موضح في الشكل 27-6.
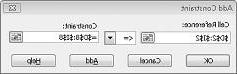
تضمن إضافة هذه القيود أنه عندما يحاول Solver مجموعات مختلفة لقيم الخلية المتغيرة، سيتم مراعاة المجموعات التي تفي بالمعلمات التالية فقط:
-
D2<=D8 (المبلغ المنتج من المخدرات 1 أقل من أو يساوي الطلب على المخدرات 1)
-
E2<=E8 (كمية المنتجة من المخدرات 2 أقل من أو يساوي الطلب على المخدرات 2)
-
F2<=F8 (المبلغ المنتج من المخدرات 3 هو أقل من أو يساوي الطلب على المخدرات 3)
-
G2<=G8 (الكمية المنتجة من المخدرات 4 هو أقل من أو يساوي الطلب على المخدرات 4)
-
H2<=H8 (المبلغ المنتج من المخدرات 5 هو أقل من أو يساوي الطلب على المخدرات 5)
-
I2<=I8 (المبلغ المنتج من المخدرات 6 هو أقل من أو يساوي الطلب على المخدرات 6)
انقر فوق موافق في مربع الحوار إضافة قيد. يجب أن تبدو نافذة Solver مثل الشكل 27-7.
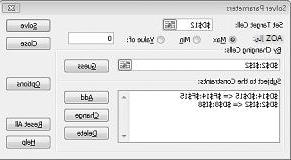
نقوم بإدخال القيد الذي يجب أن يكون تغيير الخلايا غير سالب في مربع الحوار خيارات Solver. انقر فوق الزر خيارات في مربع الحوار معلمات Solver. حدد المربع افتراض نموذج خطي والمربع افتراض غير سالب، كما هو موضح في الشكل 27-8 في الصفحة التالية. انقر فوق "موافق".
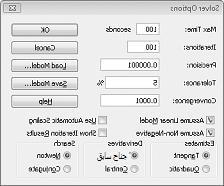
يضمن تحديد المربع افتراض غير سالب أن Solver يأخذ في الاعتبار فقط مجموعات الخلايا المتغيرة التي تفترض فيها كل خلية متغيرة قيمة غير سالبة. لقد حددنا المربع افتراض نموذج خطي لأن مشكلة مزيج المنتج هي نوع خاص من مشكلة Solver تسمى نموذج خطي. بشكل أساسي، نموذج Solver خطي في ظل الشروط التالية:
-
يتم حساب الخلية الهدف عن طريق إضافة شروط النموذج معا (تغيير الخلية)*(ثابت).
-
يفي كل قيد ب "متطلبات النموذج الخطي". وهذا يعني أنه يتم تقييم كل قيد عن طريق إضافة شروط النموذج معا (تغيير الخلية)*(ثابت) ومقارنة المبالغ بالثابت.
لماذا تكون مشكلة Solver هذه خطية؟ يتم حساب الخلية المستهدفة (الربح) على أنها
(المخدرات 1 الربح لكل جنيه)*(المخدرات 1 جنيه المنتجة) + (المخدرات 2 الربح لكل جنيه)*(المخدرات 2 جنيه المنتجة) + ... (المخدرات 6 الربح لكل جنيه)*(المخدرات 6 جنيه المنتجة)
يتبع هذا الحساب نمطا يتم فيه اشتقاق قيمة الخلية الهدف عن طريق إضافة مصطلحات النموذج معا (خلية متغيرة)*(ثابت).
يتم تقييم قيد العمل لدينا من خلال مقارنة القيمة المشتقة من (العمالة المستخدمة لكل رطل من المخدرات 1)*(المخدرات 1 جنيه تنتج) + (العمالة المستخدمة لكل جنيه من المخدرات 2)*(المخدرات 2 جنيه تنتج)+ ... (العمالة لناed لكل رطل من المخدرات 6)*(المخدرات 6 جنيه تنتج) إلى العمالة المتاحة.
لذلك، يتم تقييم قيد العمل عن طريق إضافة شروط النموذج معا (تغيير الخلية)*(ثابت) ومقارنة المبالغ بالثابت. يلبي كل من قيد العمل وقيد المواد الخام متطلبات النموذج الخطي.
تأخذ قيود الطلب الخاصة بنا الشكل
(المخدرات 1 المنتجة)<=(الطلب على المخدرات 1) (المخدرات 2 المنتجة)<=(الطلب على المخدرات 2) §(المخدرات 6 المنتجة)<=(الطلب على المخدرات 6)
يفي كل قيد طلب أيضا بمتطلبات النموذج الخطي، لأنه يتم تقييم كل منها عن طريق إضافة شروط النموذج معا (خلية متغيرة)*(ثابت) ومقارنة المبالغ بالثابت.
بعد أن أظهرنا أن نموذج مزيج منتجاتنا هو نموذج خطي، لماذا يجب أن نهتم؟
-
إذا كان نموذج Solver خطيا وحددنا افتراض نموذج خطي، فإن Solver مضمون للعثور على الحل الأمثل لنموذج Solver. إذا لم يكن نموذج Solver خطيا، فقد يجد Solver الحل الأمثل أو لا يعثر عليه.
-
إذا كان نموذج Solver خطيا وحددنا افتراض نموذج خطي، فإن Solver يستخدم خوارزمية فعالة جدا (طريقة بسيطة) للعثور على الحل الأمثل للنموذج. إذا كان نموذج Solver خطيا ولم نحدد افتراض نموذج خطي، فإن Solver يستخدم خوارزمية غير فعالة جدا (أسلوب GRG2) وقد تواجه صعوبة في العثور على الحل الأمثل للنموذج.
بعد النقر فوق موافق في مربع الحوار خيارات Solver، سنعود إلى مربع الحوار Solver الرئيسي، الموضح سابقا في الشكل 27-7. عند النقر فوق حل، تحسب Solver الحل الأمثل (إذا كان موجودا) لنموذج مزيج منتجاتنا. كما ذكرت في الفصل 26، فإن الحل الأمثل لنموذج مزيج المنتج سيكون مجموعة من قيم الخلايا المتغيرة (جنيهات تنتج من كل دواء) التي تزيد من الربح على مجموعة من جميع الحلول الممكنة. مرة أخرى، الحل الممكن هو مجموعة من قيم الخلايا المتغيرة التي تفي بجميع القيود. تعد قيم الخلايا المتغيرة الموضحة في الشكل 27-9 حلا ممكنا لأن جميع مستويات الإنتاج غير سالبة، ومستويات الإنتاج لا تتجاوز الطلب، ولا يتجاوز استخدام الموارد الموارد المتاحة.
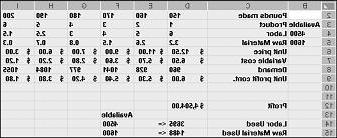
تمثل قيم الخلايا المتغيرة الموضحة في الشكل 27-10 في الصفحة التالية حلا غير قابل للتطبيق للأسباب التالية:
-
نحن ننتج أكثر من المخدرات 5 من الطلب عليه.
-
نحن نستخدم عمالة أكثر مما هو متاح.
-
نحن نستخدم مواد خام أكثر مما هو متاح.
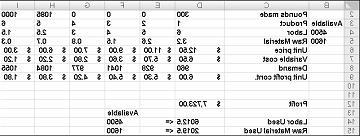
بعد النقر فوق حل، تعثر Solver بسرعة على الحل الأمثل الموضح في الشكل 27-11. تحتاج إلى تحديد الاحتفاظ بحل Solver للحفاظ على قيم الحل الأمثل في ورقة العمل.
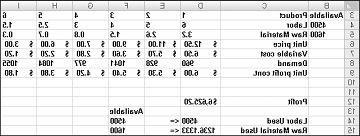
يمكن لشركة الأدوية لدينا تعظيم أرباحها الشهرية على مستوى 6625.20 دولار من خلال إنتاج 596.67 جنيه من المخدرات 4، 1084 جنيه من المخدرات 5، وليس أي من المخدرات الأخرى! لا يمكننا تحديد ما إذا كان يمكننا تحقيق أقصى ربح قدره 6625.20 دولارا بطرق أخرى. كل ما يمكننا التأكد منه هو أنه مع محدودية مواردنا والطلب، لا توجد طريقة لجعل أكثر من 6627.20 دولار هذا الشهر.
لنفترض أنه يجب تلبية الطلب على كل منتج. (راجع ورقة عمل "لا يوجد حل ممكن" في الملف Prodmix.xlsx.) ثم علينا تغيير قيود الطلب لدينا من D2:I2<=D8:I8 إلى D2:I2>=D8:I8. للقيام بذلك، افتح Solver، وحدد القيد D2:I2<=D8:I8، ثم انقر فوق تغيير. يظهر مربع الحوار تغيير القيد، الموضح في الشكل 27-12.
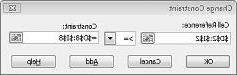
حدد >=، ثم انقر فوق موافق. لقد تأكدنا الآن من أن Solver سينظر في تغيير قيم الخلايا التي تلبي جميع الطلبات فقط. عند النقر فوق حل، سترى الرسالة "تعذر على Solver العثور على حل ممكن". لا تعني هذه الرسالة أننا ارتكبنا خطأ في نموذجنا، ولكن بدلا من ذلك، مع مواردنا المحدودة، لا يمكننا تلبية الطلب على جميع المنتجات. Solver يخبرنا ببساطة أنه إذا أردنا تلبية الطلب على كل منتج، فإننا بحاجة إلى إضافة المزيد من العمالة أو المزيد من المواد الخام أو أكثر من كليهما.
دعونا نرى ما يحدث إذا سمحنا بطلب غير محدود على كل منتج ونسمح بإنتاج كميات سلبية من كل دواء. (يمكنك رؤية مشكلة Solver هذه في ورقة عمل تعيين القيم عدم التقارب في الملف Prodmix.xlsx.) للعثور على الحل الأمثل لهذا الموقف، افتح Solver، وانقر فوق الزر خيارات، ثم قم بإلغاء تحديد المربع افتراض غير سالب. في مربع الحوار معلمات Solver، حدد قيد الطلب D2:I2<=D8:I8 ثم انقر فوق حذف لإزالة القيد. عند النقر فوق حل، يقوم Solver بإرجاع الرسالة "تعيين قيم الخلية لا تتقارب". تعني هذه الرسالة أنه إذا كان سيتم تكبير الخلية الهدف (كما هو الحال في مثالنا)، فهناك حلول ممكنة ذات قيم خلايا مستهدفة كبيرة بشكل عشوائي. (إذا كان من المقرر تصغير الخلية الهدف، فإن الرسالة "تعيين قيم الخلايا لا تتلاقى" تعني وجود حلول ممكنة ذات قيم خلايا مستهدفة صغيرة بشكل عشوائي.) في حالتنا، من خلال السماح بإنتاج سلبي لدواء، نحن في الواقع "خلق" الموارد التي يمكن استخدامها لإنتاج كميات كبيرة بشكل تعسفي من الأدوية الأخرى. نظرا لطلبنا غير المحدود، يسمح لنا هذا بجني أرباح غير محدودة. في وضع حقيقي، لا يمكننا أن نجني كمية لا نهائية من المال. باختصار، إذا رأيت "تعيين القيم لا تتقارب"، فإن النموذج الخاص بك لديه خطأ.
-
لنفترض أن شركة الأدوية لدينا يمكنها شراء ما يصل إلى 500 ساعة من العمالة بمبلغ 1 دولار في الساعة أكثر من تكاليف العمالة الحالية. كيف يمكننا زيادة الربح إلى أقصى حد؟
-
في مصنع تصنيع الرقائق، ينتج أربعة فنيين (A وB وC وD) ثلاثة منتجات (المنتجات 1 و2 و3). هذا الشهر، يمكن للشركة المصنعة للشرائح بيع 80 وحدة من المنتج 1، و50 وحدة من المنتج 2، وعلى الأكثر 50 وحدة من المنتج 3. يمكن للفني أ صنع المنتجات 1 و3 فقط. يمكن للفني ب صنع المنتجات 1 و2 فقط. يمكن للفني C إنشاء المنتج 3 فقط. يمكن للفني D إنشاء المنتج 2 فقط. لكل وحدة يتم إنتاجها، تساهم المنتجات بالربح التالي: المنتج 1، 6 دولارات؛ المنتج 1، 6 دولار؛ المنتج 1، 6 دولار؛ المنتج 1، 6 دولار؛ المنتج 1، 6 دولار؛ المنتج 1، 6 دولار؛ المنتج 1، المنتج 2، 7 دولارات؛ والمنتج 3، 10 دولارات. الوقت (بالساعات) الذي يحتاجه كل فني لتصنيع منتج هو كما يلي:
المنتج
الفني أ
الفني ب
الفني C
الفني D
1
2
2,5
لا يمكن القيام به
لا يمكن القيام به
2
لا يمكن القيام به
3
لا يمكن القيام به
3,5
3
3
لا يمكن القيام به
4
لا يمكن القيام به
-
يمكن لكل فني العمل لمدة تصل إلى 120 ساعة شهريا. كيف يمكن للشركة المصنعة للرقاقة زيادة أرباحها الشهرية إلى أقصى حد؟ افترض أنه يمكن إنتاج عدد كسري من الوحدات.
-
تنتج محطة تصنيع الكمبيوتر أجهزة الماوس ولوحات المفاتيح وعصا التحكم الخاصة بلعبة الفيديو. يتم إعطاء الربح لكل وحدة، واستخدام العمالة لكل وحدة، والطلب الشهري، واستخدام الوقت الآلي لكل وحدة في الجدول التالي:
ماوس
لوحات مفاتيح
المقود
الربح/الوحدة
8 دولارات
11 دولارا
9 دولارات
استخدام/وحدة العمل
.2 ساعة
.3 ساعة
.24 ساعة
وقت/وحدة الجهاز
.04 ساعة
.055 ساعة
.04 ساعة
الطلب الشهري
15,000
27,000
11,000
-
كل شهر، يتوفر ما مجموعه 13,000 ساعة عمل و3000 ساعة من وقت الجهاز. كيف يمكن للشركة المصنعة زيادة مساهمتها الشهرية من المصنع إلى أقصى حد؟
-
حل مثال المخدرات لدينا على افتراض أنه يجب تلبية الحد الأدنى من الطلب على 200 وحدة لكل دواء.
-
جيسون يجعل أساور الماس والقلادات والأقراط. يريد أن يعمل بحد أقصى 160 ساعة شهريا. لديه 800 أونصة من الماس يتم إعطاء الأرباح ووقت العمل والأونصات من الماس المطلوب لإنتاج كل منتج أدناه. إذا كان الطلب على كل منتج غير محدود، كيف يمكن لجايسون زيادة أرباحه إلى أقصى حد؟
المنتج
ربح الوحدة
ساعات العمل لكل وحدة
أوقية من الماس لكل وحدة
سوار
300 ر.س
.35
1,2
قلادة
200 ر.س.
.15
.75
اقراط
100 ر.س
.05
.5










