LINREGRESE (funkce)

Popis

Funkce LINREGRESE vypočítá pomocí metody nejmenších čtverců statistické hodnoty pro přímku, která nejlépe odpovídá uvedeným datům, a vrátí matici s parametry přímky. Funkci LINREGRESE lze také použít společně s dalšími funkcemi, které vypočtou statistické hodnoty pro další typy lineárních modelů s neznámými parametry, včetně polynomických, logaritmických, exponenciálních nebo mocninných řad. Vzhledem k tomu, že tato funkce vrací matici hodnot, musí být zadána jako maticový vzorec. Pokyny jsou uvedeny u příkladů v tomto článku.

Tato přímka je definována následujícím vztahem:

y = mx + b

– nebo –

y = m1x1 + m2x2 + ... + b

pokud existuje více oblastí x, kde závislé hodnoty y jsou funkcí nezávislých hodnot x. Hodnoty m jsou koeficienty odpovídající každé z hodnot x, b je konstanta. Všimněte si, že y, x a m mohou být vektory. Matice, která je výsledkem funkce LINREGRESE, má tvar {mn;mn-1;...;m1;b}. Funkce LINREGRESE může také vracet další regresní statistiky.

Syntaxe

LINREGRESE(pole_y;[pole_x];[b];[stat])

Syntaxe funkce LINREGRESE má následující argumenty:

Syntaxe

• Pole_y:    Povinný argument. Sada hodnot y odvozených ze vztahu y = mx + b.

  • Pokud je oblast pole_y v jediném sloupci, je každý sloupec oblasti pole_x interpretován jako samostatná proměnná.

  • Pokud je oblast pole_y v jediném řádku, je každý řádek oblasti pole_x interpretován jako samostatná proměnná.

• Pole_x:    Nepovinný argument. Sada hodnot x, které již mohou být známé ze vztahu y = mx + b.

  • Oblast known_x může zahrnovat jednu nebo více sad proměnných. Pokud se použije jenom jedna proměnná, known_y a known_x mohou být oblasti libovolného obrazce, pokud mají stejné rozměry. Pokud je použito více proměnných, known_y musí být vektor (to znamená oblast s výškou jednoho řádku nebo šířkou jednoho sloupce).

  • Pokud vynecháte argument pole_x, předpokládá se, že jde o matici {1;2;3;...}, která je stejně velká jako pole_y.

• B:    Volitelný argument. Logická hodnota, která určuje, zda se má parametr b (absolutní člen) počítat nebo zda se má rovnat nule.

  • Pokud má argument b hodnotu PRAVDA nebo není uveden, počítá se konstanta b běžným způsobem.

  • Jestliže má argument b hodnotu NEPRAVDA, uvažuje se, že b = 0, a hodnoty m se upraví tak, aby platilo y = mx.

• Stat:    Volitelný argument. Jedná se o logickou hodnotu, která určuje, zda chcete zjistit další regresní statistiky.

  • Pokud je hodnota statistika PRAVDA, vrátí funkce LINEST další regresní statistiku. Výsledkem je, že vrácená matice je {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r²,sey; F,df;ssreg,ssresid}.

  • V případě, že je argument stat NEPRAVDA nebo není uveden, vrátí funkce LINREGRESE pouze koeficienty m a konstantu b.

    Dodatečné regresní statistiky jsou:

Následující příklad uvádí pořadí, ve kterém se vracejí dodatečné regresní statistiky.

Poznámky

• Libovolnou přímku lze popsat pomocí sklonu a průsečíku s osou y:

  Sklon (m):
  Pokud chcete najít sklon čáry, často napsané jako m, vezměte na čáru dva body (x1;y1) a (x2;y2); sklon se rovná (y2 - y1)/(x2 - x1).

  Y-intercept (b):
  Zachycování y čáry, často napsané jako b, je hodnota y v místě, kde čára protíná osu y.

  Rovnice přímky je y = mx + b. Jakmile znáte hodnoty m a b, můžete vypočítat libovolný bod této přímky tak, že do rovnice dosadíte hodnotu x nebo y. Lze též použít funkci LINTREND.

• Máte-li pouze jedinou nezávislou proměnnou x, můžete hodnoty sklonu a průsečíku s osou y získat přímo z následujících vzorců:

  Sklon:
  =INDEX(LINEST(known_y,known_x's);1)

  Y-intercept:
  =INDEX(LINEST(known_y,known_x's);2)

• Přesnost přímky vypočtené funkcí LINREGRESE závisí na tom, jak je daná množina dat rozptýlená. Čím více jsou data lineární, tím je regresní model funkce LINREGRESE přesnější. Funkce LINREGRESE používá metodu nejmenších čtverců, aby se regrese co nejvíce přiblížila daným datům. Máte-li pouze jedinou nezávislou proměnnou x, budou se m a b počítat podle následujících vzorců:

  

  

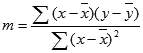
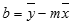
  kde x a y jsou střední hodnoty výběru, např. x = PRŮMĚR (pole_x) a y = PRŮMĚR(pole_y).

• Funkce tvarování čar a křivek FUNKCE LINEST a LOGEST počítají nejlepší přímku nebo exponenciální křivku, která odpovídá vašim datům. Musíte se ale rozhodnout, který ze dvou výsledků nejlépe vyhovuje vašim datům. Pro přímku known_y můžete vypočítat hodnotu TREND( known_x) nebo FUNKCERŮST(known_y,known_x)pro exponenciální křivku. Tyto funkce bez argumentu new_x vrátí matici hodnot y předpovídanou podél této čáry nebo křivky ve skutečných datových bodech. Předpokládané hodnoty pak můžete porovnat se skutečnými hodnotami. Můžete je chtít namapovat pro vizuální porovnání.

• U regresní analýzy počítá aplikace Excel pro každý bod druhou mocninu rozdílu mezi skutečnou hodnotou y v tomto bodě a hodnotou odhadnutou. Součet těchto kvadratických odchylek se nazývá reziduální součet čtverců ssresid. Aplikace Excel pak vypočítá celkový součet čtverců, sstotal. Pokud je argument b = PRAVDA nebo chybí, rovná se celkový součet čtverců součtu kvadratických odchylek mezi skutečnými hodnotami y a průměrem hodnot y. Pokud je argument b = NEPRAVDA, je celkový součet čtverců součtem čtverců skutečných hodnot y (bez odečtení průměrných hodnot y od každé jednotlivé hodnoty y). Regresní součet čtverců ssreg lze vypočítat jako ssreg = sstotal - ssredid. Čím menší je zbytkový součet čtverců, ve srovnání s celkovým součtem čtverců, tím větší je hodnota koeficientu určení, r², což je indikátor toho, jak dobře se rovnice vyplývající z regresní analýzy vysvětluje vztah mezi proměnnými. Hodnota r^{2 se rovná} ssreg/sstotal.

• V některých případech jeden nebo více sloupců X (předpokládá se, že sloupce Y a X jsou ve sloupcích) nemusí mít v přítomnosti ostatních sloupců X žádnou další prediktivní hodnotu. Jinými slovy, odstranění jednoho nebo více sloupců X může vést k stejně přesným předpovídání hodnot Y. V takovém případě by tyto redundantní sloupce X měly být z regresního modelu vynechány. Tento jev se nazývá "kolinearity", protože libovolný redundantní sloupec X může být vyjádřen jako součet násobků ne redundantních sloupců X. Funkce LINEST vyhledá kolinearitu a odebere všechny redundantní sloupce X z regresního modelu, když je identifikuje. Odebrané sloupce X lze ve výstupu LINEST rozpoznat jako sloupce s 0 koeficienty kromě hodnot 0 se. Pokud se jeden nebo více sloupců odebere jako redundantní, bude mít df vliv, protože df závisí na počtu sloupců X, které se skutečně používají pro prediktivní účely. Podrobnosti o výpočtu df najdete v příkladu 4. Pokud se df změní, protože jsou odebrány nadbytečné sloupce X, budou ovlivněny také hodnoty sey a F. V praxi by měla být kolinearita relativně vzácná. Jeden případ, ve kterém je větší pravděpodobnost, že vznikne, je, když některé sloupce X obsahují jenom 0 a 1 hodnoty jako indikátory toho, jestli předmět v experimentu je nebo není členem určité skupiny. Pokud argument b = PRAVDA nebo je vynechán, funkce LINEST efektivně vloží další sloupec X všech hodnot 1, aby se odchyt vymodeluje. Pokud máte sloupec s hodnotou 1 pro každý předmět, pokud je muž, nebo 0, pokud ne, a máte také sloupec s hodnotou 1 pro každý předmět, pokud je žena, nebo 0, pokud ne, je tento druhý sloupec nadbytečný, protože položky v tomto sloupci lze získat odečítáním položky ve sloupci "indikátor muže" od položky v dalším sloupci všech 1 hodnot přidaných funkcí LINEST.

• Pokud nejsou z modelu odebrány žádné sloupce X z důvodu kolinearity, vypočítá se hodnota df následujícím způsobem: existuje-li k sloupců obsahujících pole_x a argument b = PRAVDA nebo chybí, pak df = n – k – 1. Jestliže argument b = NEPRAVDA, pak df = n - k. V obou případech zvyšuje každý sloupec X odebraný z důvodu kolinearity hodnotu df o 1.

• Zadáváte-li jako argument maticovou konstantu (například pole_x), oddělujte hodnoty v řádku středníky a jednotlivé řádky symboly svislé čáry (|). Oddělovače se mohou lišit podle místního nastavení.

• Všimněte si, že hodnoty y, předpovídané pomocí regresní rovnice, nemusí platit, pokud jsou mimo oblast hodnot y, pomocí kterých jste rovnici vytvářeli.

• Algoritmus použitý u funkce LINREGRESE se odlišuje od algoritmu použitého u funkcí INTERCEPT a SLOPE. U neurčitých dat ležících na stejné přímce může rozdíl mezi těmito algoritmy vést k odlišným výsledkům. Jsou-li například datové body argumentu pole_y rovny 0 a datové body argumentu pole_x rovny 1, jsou výsledky následující:

  • Funkce LINREGRESE vrátí hodnotu 0. Algoritmus funkce LINREGRESE vrací přijatelné výsledky pro data ležící na stejné přímce, přičemž v tomto případě lze nalézt alespoň jeden výsledek.

  • SLOPE a INTERCEPT vrátí #DIV/0! . Algoritmus funkcí SLOPE a INTERCEPT je navržený tak, aby vypadal jenom pro jednu odpověď, a v tomto případě může být více odpovědí.

• Kromě použití funkce LOGEST k výpočtu statistik pro jiné regresní typy můžete pomocí funkce LINEST vypočítat oblast jiných regresních typů zadáním funkcí proměnných x a y jako řady x a y pro funkci LINEST. Například následující vzorec:

  =LINREGRESE(hodnoty_y;hodnoty_x^SLOUPEC($A:$C))

  funguje, pokud máte jeden sloupec s hodnotami y a jeden sloupec s hodnotami x, které počítají kubickou aproximaci (polynom 3. stupně) ve tvaru:

  y = m1*x + m2*x^2 + m3*x^3 + b

  Tento vzorec lze upravit a počítat jiné typy regrese. V některých případech však vyžaduje úpravu výstupních hodnot a dalších statistických údajů.

• Hodnota F-testu vrácená funkcí LINREGRESE se liší od hodnoty F-testu vrácené funkcí FTEST. Funkce LINREGRESE vrátí F-statistiku, zatímco funkce FTEST vrátí pravděpodobnost.

Příklady