Gibt Wahrscheinlichkeiten einer binomialverteilten Zufallsvariablen zurück. Verwenden Sie BINOMVERT bei Problemen mit einer festgelegten Anzahl von Tests oder Versuchen, wenn das Ergebnis jedes einzelnen Versuchs entweder Erfolg oder Misserfolg ist, die einzelnen Versuche voneinander unabhängig sind und die Wahrscheinlichkeit des Erfolgs für alle Versuche konstant ist. Mit BINOMVERT lässt sich beispielsweise die Wahrscheinlichkeit ermitteln, mit der zwei von drei Neugeborenen männlich sind.
Wichtig: Diese Funktion wurde durch eine oder mehrere neue Funktionen ersetzt, die ggf. eine höhere Genauigkeit bieten und deren Namen die Verwendung besser wiedergeben. Obwohl diese Funktion aus Gründen der Abwärtskompatibilität weiterhin verfügbar ist, sollten Sie von nun an die neuen Funktionen verwenden, da die alte Funktion in zukünftigen Versionen von Excel möglicherweise nicht mehr verfügbar sein wird.
Weitere Informationen zur neuen Funktion finden Sie unter BINOM.VERT (Funktion).
Syntax
BINOMVERT(Zahl_Erfolge;Versuche;Erfolgswahrsch;Kumuliert)
Die Syntax der Funktion BINOMVERT weist die folgenden Argumente auf:
-
Zahl_Erfolge Erforderlich. Die Anzahl der Erfolge in einer Versuchsreihe.
-
Versuche Erforderlich. Die Anzahl der voneinander unabhängigen Versuche.
-
Erfolgswahrsch Erforderlich. Die Wahrscheinlichkeit eines Erfolgs für jeden Versuch.
-
Kumuliert Erforderlich. Ein Wahrheitswert, der die Form der Funktion bestimmt. Ist Kumuliert mit WAHR angegeben, gibt BINOMIST die Verteilungsfunktion zurück, die die Wahrscheinlichkeit angibt, dass es in den meisten number_s gibt. Ist die Funktion FALSCH, gibt sie die Wahrscheinlichkeitsfunktion einer Massenfunktion zurück, die die Wahrscheinlichkeit angibt, dass es number_s gibt.
Hinweise
-
Zahl_Erfolge und Versuche werden auf ganze Zahlen abgerundet.
-
Ist Zahl_Erfolge, Versuche oder Erfolgswahrsch nichtnumerisch, gibt BINOMVERT den Fehlerwert #WERT! zurück.
-
Ist Zahl_Erfolge < 0 oder Zahl_Erfolge > Versuche, gibt BINOMVERT den Fehlerwert #ZAHL! zurück.
-
Ist Erfolgswahrsch < 0 oder Erfolgswahrsch > 1, gibt BINOMVERT den Fehlerwert #ZAHL! zurück.
-
Ist x = Zahl_Erfolge, n = Versuche und p = Erfolgswahrsch, sieht die binomiale Wahrscheinlichkeitsfunktion wie folgt aus:
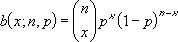
wobei:
KOMBINATIONEN(n;x) ist.
-
Ist x = Zahl_Erfolge, n = Versuche und p = Erfolgswahrsch, sieht die kumulative binomiale Verteilung wie folgt aus:
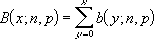
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Daten |
Beschreibung |
|
|
6 |
Anzahl der Erfolge in einer Versuchsreihe |
|
|
10 |
Anzahl der voneinander unabhängigen Versuche |
|
|
0,5 |
Wahrscheinlichkeit eines Erfolgs für jeden Versuch |
|
|
Formel |
Beschreibung |
Ergebnis |
|
=BINOMVERT(A2;A3;A4;FALSCH) |
Wahrscheinlichkeit, dass genau 6 von 10 Versuchen Erfolge sind. |
0,2050781 |
