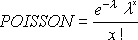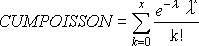Gibt Wahrscheinlichkeiten einer poissonverteilten Zufallsvariablen zurück. Eine übliche Anwendung der Poissonverteilung ist die Modellierung der Anzahl der Ereignisse innerhalb eines bestimmten Zeitraumes, beispielsweise die Anzahl der Bankkunden, die innerhalb einer Stunde an einem Geldautomaten eintreffen.
Wichtig: Diese Funktion wurde durch eine oder mehrere neue Funktionen ersetzt, die ggf. eine höhere Genauigkeit bieten und deren Namen die Verwendung besser wiedergeben. Obwohl diese Funktion aus Gründen der Abwärtskompatibilität weiterhin verfügbar ist, sollten Sie von nun an die neuen Funktionen verwenden, da die alte Funktion in zukünftigen Versionen von Excel möglicherweise nicht mehr verfügbar sein wird.
Weitere Informationen zur neuen Funktion finden Sie unter POISSON.VERT (Funktion).
Syntax
POISSON(x;Mittelwert;Kumuliert)
Die Syntax der Funktion POISSON weist die folgenden Argumente auf:
-
x Erforderlich. Die Zahl der Fälle
-
Mittelwert Erforderlich. Der erwartete Zahlenwert
-
Kumuliert Erforderlich. Ein logischer Wert, der die Form der zurückgegebenen Wahrscheinlichkeitsverteilung bestimmt. Wenn kumulativ TRUE ist, gibt POISSON die kumulative Poisson-Wahrscheinlichkeit zurück, dass die Anzahl der zufälligen Ereignisse zwischen null und x einschließlich liegt; False gibt die Poisson-Wahrscheinlichkeits-Massenfunktion zurück, dass die Anzahl der ereignisse genau x ist.
Hinweise
-
Ist x keine ganze Zahl, werden die Nachkommastellen abgeschnitten.
-
Wenn x oder mean nicht numerisch ist, gibt POISSON die #VALUE! zurückgegeben.
-
Wenn x < 0 ist, gibt POISSON die #NUM! zurückgegeben.
-
Wenn mean < 0, gibt POISSON die #NUM! zurückgegeben.
-
POISSON berechnet die folgenden Formeln.
Für Kumuliert = FALSCH:
Für Kumuliert = WAHR:
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Daten |
Beschreibung |
|
|
2 |
Anzahl von Ereignissen |
|
|
5 |
Erwarteter Mittelwert |
|
|
Formel |
Beschreibung (Ergebnis) |
Ergebnis |
|
=POISSON(A2;A3;WAHR) |
Kumulierte Poisson-Wahrscheinlichkeit bei den obigen Bedingungen (0,124652) |
0,124652 |
|
=POISSON(A2;A3;FALSCH) |
Die Poisson-Wahrscheinlichkeitsfunktion bei den obigen Bedingungen (0,084224) |
0,084224 |