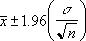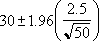Devuelve el intervalo de confianza para la media de una población con una distribución normal. El intervalo de confianza es un intervalo situado a cada lado de la media de una muestra. Por ejemplo, si solicitas un producto por correo, puedes determinar, con un nivel de confianza determinado, que llegará el producto más pronto y el más reciente.
Sintaxis
INTERVALO.CONFIANZA(alfa;standard_dev;tamaño)
Alfa es el nivel de significancia que se usa para calcular el nivel de confianza. El nivel de confianza es igual a 100*(1 - alfa)%, es decir, un alfa de 0,05 indica un nivel de confianza del 95%.
Desv_estándar es la desviación estándar de la población para el rango de datos y se supone que es conocida.
Tamaño es el tamaño de la muestra.
Comentarios
-
Si uno de los argumentos no es numérico, INTERVALO.CONFIANZA devuelve el #VALUE! o #VALOR!.
-
Si alfa ≤ 0 o alfa ≥ 1, INTERVALO.CONFIANZA devuelve el #NUM! o #VALOR!.
-
Si standard_dev ≤ 0, INTERVALO.CONFIANZA devuelve el #NUM! o #VALOR!.
-
Si el argumento tamaño no es un entero, se trunca.
-
Si el tamaño < 1, INTERVALO.CONFIANZA devuelve el #NUM! o #VALOR!.
-
Si suponemos que el argumento alfa es igual a 0,05, se tendrá que calcular el área debajo de la curva normal estándar que es igual a (1 - alfa) o 95%. Este valor es ± 1,96. Por lo tanto, el intervalo de confianza es:
Ejemplo
Suponga que observamos que, en nuestra muestra de 50 viajeros, la longitud media de un viaje al trabajo es de 30 minutos, con una desviación estándar de la población de 2,5. Podemos estar 95 por ciento seguros de que la media de la población está en el intervalo:
|
Alfa |
Desvest |
Tamaño |
Fórmula |
Descripción (resultado) |
|---|---|---|---|---|
|
0,05 |
,5 |
50 |
=INTERVALO.CONFIANZA([Alfa];[DesvEst];[Tamaño]) |
Intervalo de confianza para la media de una población. En otras palabras, la duración media de los viajes al trabajo es igual a 30 ± 0,692951 minutos, o de 29,3 a 30,7 minutos. (0.692951) |