Importante: El soporte técnico para Office 2016 y Office 2019 finalizará el 14 de octubre de 2025. Actualice a Microsoft 365 para trabajar en cualquier lugar desde cualquier dispositivo y seguir recibiendo soporte técnico. Obtener Microsoft 365
En este artículo se describe el uso de Solver, un programa de complemento de Microsoft Excel que puede usar para el análisis de hipótesis, con el fin de determinar una combinación de productos óptima.
¿Cómo puedo determinar la combinación de productos mensual que maximiza la rentabilidad?
Las empresas a menudo necesitan determinar la cantidad de cada producto para producir mensualmente. En su forma más sencilla, el problema de la mezcla de productos implica cómo determinar la cantidad de cada producto que se debe producir durante un mes para maximizar los beneficios. Por lo general, la mezcla de productos debe cumplir las siguientes restricciones:
-
La combinación de productos no puede usar más recursos de los que están disponibles.
-
Hay una demanda limitada para cada producto. No podemos producir más de un producto durante un mes del que dicta la demanda, porque el exceso de producción se desperdicia (por ejemplo, un medicamento perecedero).
Ahora vamos a resolver el siguiente ejemplo del problema de la mezcla de productos. Usted puede encontrar la solución a este problema en el archivo Prodmix.xlsx, que se muestra en la figura 27-1.
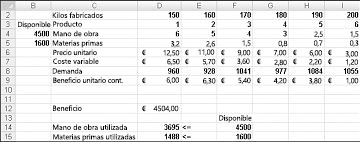
Supongamos que trabajamos para una empresa farmacéutica que produce seis productos diferentes en su planta. La producción de cada producto requiere mano de obra y materia prima. La fila 4 de la Figura 27-1 muestra las horas de trabajo necesarias para producir una libra de cada producto, y la fila 5 muestra las libras de materia prima necesarias para producir una libra de cada producto. Por ejemplo, producir una libra del producto 1 requiere seis horas de trabajo y 3,2 libras de materia prima. Para cada medicamento, el precio por libra se da en la fila 6, el costo unitario por libra se da en la fila 7, y la contribución a beneficios por libra se da en la fila 9. Por ejemplo, el producto 2 se vende por 11,00 $ por libra, incurre en un costo unitario de 5,70 $ por libra y contribuye a 5,30 $ de beneficio por libra. La demanda del mes para cada medicamento se da en la fila 8. Por ejemplo, la demanda del producto 3 es de 1041 libras. Este mes, 4500 horas de trabajo y 1600 libras de materia prima están disponibles. ¿Cómo puede esta empresa maximizar sus beneficios mensuales?
Si no sabíamos nada de Solver de Excel, atacaríamos este problema creando una hoja de cálculo para realizar un seguimiento de los beneficios y el uso de recursos asociados a la combinación de productos. A continuación, usaríamos prueba y error para variar la mezcla de productos para optimizar los beneficios sin usar más mano de obra o materia prima de la que está disponible, y sin producir ningún medicamento en exceso de demanda. Usamos Solver en este proceso solo en la fase de prueba y error. Básicamente, Solver es un motor de optimización que realiza la búsqueda de prueba y error a la perfección.
Una clave para resolver el problema de la mezcla de productos es calcular de forma eficiente el uso de recursos y los beneficios asociados con cualquier combinación de productos determinada. Una herramienta importante que podemos usar para hacer este cálculo es la función SUMAPRODUCTO. La función SUMAPRODUCTO multiplica los valores correspondientes en rangos de celdas y devuelve la suma de esos valores. Cada rango de celdas usado en una SUMAPRODUCTO evaluación debe tener las mismas dimensiones, lo que implica que puede usar SUMAPRODUCTO con dos filas o dos columnas, pero no con una columna y una fila.
Como ejemplo de cómo podemos usar la función SUMAPRODUCTO en nuestro ejemplo de combinación de productos, vamos a intentar calcular nuestro uso de recursos. Nuestro uso de la mano de obra se calcula mediante
(Mano de obra usada por libra de la droga 1)*(Medicamento 1 libras producidas)+ (Mano de obra usada por libra de la droga 2)*(Droga 2 libras producidas) + ... (Mano de obra usada por libra de la droga 6)*(Medicamento 6 libras producidas)
Podríamos calcular el uso de la mano de obra de forma más tediosa como D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Del mismo modo, el uso de materias primas podría calcularse como D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Sin embargo, escribir estas fórmulas en una hoja de cálculo para seis productos requiere mucho tiempo. Imagine cuánto tiempo tardaría si estuviera trabajando con una empresa que produjo, por ejemplo, 50 productos en su planta. Una forma mucho más sencilla de calcular el uso de la mano de obra y la materia prima es copiar de D14 a D15 la fórmula SUMAPRODUCTO($D$2:$I$2,D4:I4). Esta fórmula calcula D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (que es nuestro uso de mano de obra), pero es mucho más fácil de especificar. Observe que uso el signo $ con el rango D2:I2 para que, al copiar la fórmula, todavía capture la mezcla de productos de la fila 2. La fórmula de la celda D15 calcula el uso de materia prima.
De manera similar, nuestros beneficios se determinan
(Beneficio de 1 medicamento por libra)*(Medicamento 1 libras producidas) + (Beneficio de drogas 2 por libra)*(Medicamento 2 libras producidas) + ... (Beneficio de drogas 6 por libra)*(Medicamento 6 libras producidas)
Los beneficios se calculan fácilmente en la celda D12 con la fórmula SUMAPRODUCTO(D9:I9,$D$2:$I$2).
Ahora podemos identificar los tres componentes de nuestro modelo solver de la mezcla de productos.
-
Celda de destino. Nuestro objetivo es maximizar los beneficios (calculados en la celda D12).
-
Cambio de celdas. El número de libras producidas de cada producto (enumerado en el rango de celdas D2:I2)
-
Restricciones. Tenemos las siguientes restricciones:
-
No uses más mano de obra ni materia prima de la que está disponible. Es decir, los valores de las celdas D14:D15 (los recursos usados) deben ser menores o iguales que los valores de las celdas F14:F15 (los recursos disponibles).
-
No produzca más de un medicamento de lo que está en demanda. Es decir, los valores de las células D2:I2 (libras producidas de cada fármaco) deben ser menores o iguales a la demanda de cada medicamento (enumerados en las células D8:I8).
-
No podemos producir una cantidad negativa de cualquier medicamento.
-
Le mostraré cómo introducir la celda de destino, el cambio de celdas y las restricciones en Solver. A continuación, todo lo que necesita hacer es hacer clic en el botón Resolver para encontrar una combinación de productos que maximiza las ganancias.
Para empezar, haga clic en la pestaña Datos y, en el grupo Análisis, haga clic en Solver.
Nota: Como se explica en el capítulo 26, "Introducción a la optimización con Excel Solver", Solver se instala haciendo clic en el botón Microsoft Office y, después, en Opciones de Excel, seguido de complementos. En la lista Administrar, haga clic en Complementos de Excel, active la casilla Complemento Solver y haga clic en Aceptar.
Aparecerá el cuadro de diálogo Parámetros de Solver, como se muestra en la figura 27-2.
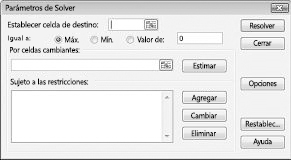
Haga clic en el cuadro Establecer celda de destino y seleccione la celda de beneficio (celda D12). Haga clic en el cuadro Cambiando celdas y seleccione el rango D2:I2, que contiene las libras producidas por cada medicamento. Ahora, el cuadro de diálogo debería tener el aspecto 27-3.
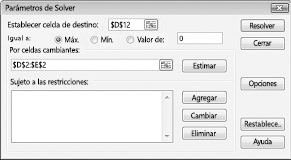
Ya estamos listos para agregar restricciones al modelo. Haga clic en el botón Agregar. Verá el cuadro de diálogo Agregar restricción, que se muestra en la figura 27-4.
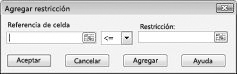
Para agregar las restricciones de uso de recursos, haga clic en el cuadro Referencia de celda y, a continuación, seleccione el rango D14:D15. Seleccione <= en la lista del medio. Haga clic en el cuadro Restricción y seleccione el rango de celdas F14:F15. El cuadro de diálogo Agregar restricción debería tener ahora el aspecto de la figura 27-5.
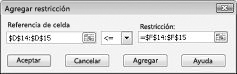
Ahora hemos asegurado que cuando Solver prueba diferentes valores para las celdas cambiantes, solo se tendrán en cuenta las combinaciones que cumplan D14<=F14 (la mano de obra usada es menor o igual que la mano de obra disponible) y D15<=F15 (la materia prima usada es menor o igual que la materia prima disponible). Haga clic en Agregar para especificar las restricciones de demanda. Rellene el cuadro de diálogo Agregar restricción como se muestra en la figura 27-6.
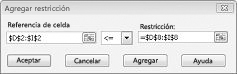
Agregar estas restricciones garantiza que, cuando Solver intente combinaciones diferentes para los valores de celda cambiantes, solo se tendrán en cuenta las combinaciones que cumplan los siguientes parámetros:
-
D2<=D8 (la cantidad producida por drug 1 es menor o igual que la demanda de Drug 1)
-
E2<=E8 (la cantidad de producto de Drug 2 es menor o igual que la demanda de Drug 2)
-
F2<=F8 (la cantidad producida por el medicamento 3 es menor o igual que la demanda de Droga 3)
-
G2<=G8 (la cantidad producida por el medicamento 4 es menor o igual que la demanda de Droga 4)
-
H2<=H8 (la cantidad producida por la droga 5 producida es menor o igual que la demanda de Droga 5)
-
I2<=I8 (la cantidad producida de La droga 6 hecha es menor o igual a la demanda de Droga 6)
Haga clic en Aceptar en el cuadro de diálogo Agregar restricción. La ventana de Solver debería tener el aspecto de la figura 27-7.
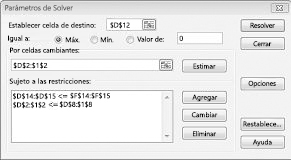
Especifique la restricción de que el cambio de celdas no debe ser negativo en el cuadro de diálogo Opciones de Solver. Haga clic en el botón Opciones del cuadro de diálogo Parámetros de Solver. Marque el cuadro Asumir modelo lineal y el cuadro Asumir no negativo, como se muestra en la figura 27-8 en la página siguiente. Haga clic en Aceptar.
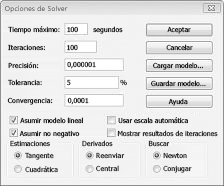
Al activar la casilla Asumir no negativo, Solver solo tiene en cuenta las combinaciones de celdas cambiantes en las que cada celda cambiante asume un valor no negativo. Hemos activado la casilla Asumir modelo lineal porque el problema de la mezcla de productos es un tipo especial de problema de Solver denominado modelo lineal. Básicamente, un modelo de Solver es lineal en las siguientes condiciones:
-
La celda de destino se calcula sumando los términos del formulario (celda cambiante)*(constante).
-
Cada restricción satisface el "requisito de modelo lineal". Esto significa que cada restricción se evalúa sumando los términos del formulario (cambiando celda)*(constante) y comparando las sumas con una constante.
¿Por qué este problema de Solver es lineal? Nuestra celda objetivo (beneficios) se calcula como
(Beneficio de 1 medicamento por libra)*(Medicamento 1 libras producidas) + (Beneficio de drogas 2 por libra)*(Medicamento 2 libras producidas) + ... (Beneficio de drogas 6 por libra)*(Medicamento 6 libras producidas)
Este cálculo sigue un patrón en el que el valor de la celda de destino se deriva sumando términos de la forma (cambiando celda)*(constante).
Nuestra restricción de mano de obra se evalúa comparando el valor derivado de (Mano de obra usada por libra de la droga 1)*(Medicamento 1 libras producidas) + (Mano de obra usada por libra de la droga 2)*(Fármaco 2 libras producidas)+ ... (Mano de obra nuestraed por libra de La droga 6)*(Medicamento 6 libras producidas) a la mano de obra disponible.
Por lo tanto, la restricción de mano de obra se evalúa sumando los términos del formulario (cambiando celda)*(constante) y comparando las sumas con una constante. Tanto la restricción de mano de obra como la restricción de materia prima cumplen el requisito de modelo lineal.
Nuestras restricciones a la demanda tienen el formato
(Droga 1 producida)<=(Demanda de drogas 1) (Droga 2 producida)<=(Demanda de drogas 2) §(Medicamento 6 producido)<=(Demanda de drogas 6)
Cada restricción de demanda también satisface el requisito de modelo lineal, ya que cada una de ellas se evalúa sumando los términos del formulario (cambiando celda)*(constante) y comparando las sumas con una constante.
Después de haber demostrado que nuestro modelo de mezcla de productos es un modelo lineal, ¿por qué deberíamos preocuparnos?
-
Si un modelo de Solver es lineal y seleccionamos Asumir modelo lineal, Solver está garantizado para encontrar la solución óptima para el modelo solver. Si un modelo de Solver no es lineal, Solver puede o no encontrar la solución óptima.
-
Si un modelo de Solver es lineal y seleccionamos Asumir modelo lineal, Solver usa un algoritmo muy eficiente (el método simple) para encontrar la solución óptima del modelo. Si un modelo de Solver es lineal y no seleccionamos Asumir modelo lineal, Solver usa un algoritmo muy ineficaz (el método GRG2) y puede tener dificultades para encontrar la solución óptima del modelo.
Después de hacer clic en Aceptar en el cuadro de diálogo Opciones de Solver, volvemos al cuadro de diálogo principal de Solver, que se muestra anteriormente en la figura 27-7. Al hacer clic en Resolver, Solver calcula una solución óptima (si existe) para nuestro modelo de mezcla de productos. Como mencioné en el Capítulo 26, una solución óptima para el modelo de mezcla de productos sería un conjunto de valores celulares cambiantes (libras producidas de cada medicamento) que maximiza los beneficios sobre el conjunto de todas las soluciones factibles. Una vez más, una solución factible es un conjunto de valores de celda que cumplen todas las restricciones. Los valores de celda cambiantes que se muestran en la Figura 27-9 son una solución factible porque todos los niveles de producción no son negativos, los niveles de producción no superan la demanda y el uso de recursos no supera los recursos disponibles.
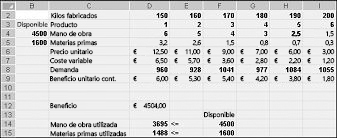
Los valores de celda cambiantes que se muestran en la figura 27-10 de la página siguiente representan una solución inviable por las siguientes razones:
-
Producimos más de Droga 5 que la demanda por ella.
-
Usamos más mano de obra de lo que está disponible.
-
Usamos más materia prima de lo que está disponible.
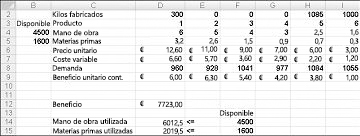
Después de hacer clic en Resolver, Solver encuentra rápidamente la solución óptima que se muestra en la figura 27-11. Debe seleccionar Mantener la solución de Solver para conservar los valores óptimos de la solución en la hoja de cálculo.
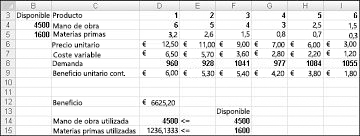
Nuestra compañía de drogas puede maximizar su ganancia mensual a un nivel de $6,625.20 al producir 596.67 libras de droga 4, 1084 libras de droga 5, y ninguna de las otras drogas! No podemos determinar si podemos obtener el máximo beneficio de 6.625,20 $ de otras maneras. Todo lo que podemos estar seguros es que con nuestros recursos limitados y demanda, no hay forma de hacer más de $6,627.20 este mes.
Suponga que es necesario satisfacer la demanda de cada producto. (Vea la hoja de cálculo Solución no factible en el Prodmix.xlsx de archivo). Después, tenemos que cambiar las restricciones de demanda de D2:I2<=D8:I8 a D2:I2>=D8:I8. Para ello, abra Solver, seleccione la restricción D2:I2<=D8:I8 y, a continuación, haga clic en Cambiar. Aparece el cuadro de diálogo Cambiar restricción, que se muestra en la figura 27-12.
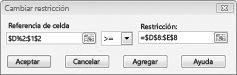
Seleccione >=y, a continuación, haga clic en Aceptar. Ahora nos aseguramos de que Solver considere la posibilidad de cambiar solo los valores de celda que cumplan todas las demandas. Al hacer clic en Resolver, verá el mensaje "Solver no ha encontrado una solución factible". Este mensaje no significa que hayamos cometido un error en nuestro modelo, sino que, con nuestros recursos limitados, no podemos satisfacer la demanda de todos los productos. Solver nos indica simplemente que si queremos satisfacer la demanda de cada producto, debemos agregar más mano de obra, más materias primas o más de ambos.
Veamos qué sucede si permitimos demanda ilimitada para cada producto y permitimos la producción de cantidades negativas de cada medicamento. (Puede ver este problema de Solver en la hoja de cálculo Establecer valores no convergentes en el Prodmix.xlsx de archivo). Para encontrar la solución óptima para esta situación, abra Solver, haga clic en el botón Opciones y desactive la casilla Asumir no negativo. En el cuadro de diálogo Parámetros de Solver, seleccione la restricción de demanda D2:I2<=D8:I8 y, a continuación, haga clic en Eliminar para quitar la restricción. Al hacer clic en Resolver, Solver devuelve el mensaje "Establecer valores de celda no convergen". Este mensaje significa que si la celda de destino se va a maximizar (como en nuestro ejemplo), hay soluciones factibles con valores de celda objetivo arbitrariamente grandes. (Si se va a minimizar la celda de destino, el mensaje "Establecer valores de celda no convergen" significa que hay soluciones factibles con valores de celda de destino reducidos arbitrariamente). En nuestra situación, al permitir la producción negativa de un medicamento, en efecto "creamos" recursos que pueden ser utilizados para producir cantidades arbitrariamente grandes de otros fármacos. Dada nuestra demanda ilimitada, esto nos permite obtener ganancias ilimitadas. En una situación real, no podemos hacer una cantidad infinita de dinero. En resumen, si ve "Establecer valores no convergen", el modelo tiene un error.
-
Supongamos que nuestra empresa farmacéutica puede comprar hasta 500 horas de trabajo a $1 más por hora que los costos de mano de obra actuales. ¿Cómo podemos maximizar los beneficios?
-
En una fábrica de chips, cuatro técnicos (A, B, C y D) producen tres productos (Productos 1, 2 y 3). Este mes, el fabricante de chips puede vender 80 unidades del Producto 1, 50 unidades del Producto 2 y, como máximo, 50 unidades del Producto 3. El técnico A solo puede hacer productos 1 y 3. El técnico B solo puede hacer productos 1 y 2. El técnico C solo puede hacer el Producto 3. El técnico D solo puede hacer el Producto 2. Por cada unidad producida, los productos aportan los siguientes beneficios: Producto 1, $6; Producto 2, $7; y producto 3, 10 $. El tiempo (en horas) que cada técnico necesita para fabricar un producto es el siguiente:
Producto
Técnico A
Técnico B
Técnico C
Técnico D
1
2
2,5
No se puede hacer
No se puede hacer
2
No se puede hacer
3
No se puede hacer
3,5
3
3
No se puede hacer
4
No se puede hacer
-
Cada técnico puede trabajar hasta 120 horas al mes. ¿Cómo puede el fabricante del chip maximizar sus ganancias mensuales? Suponga que se puede producir un número fraccionario de unidades.
-
Una planta de fabricación de equipos produce ratones, teclados y joysticks de videojuegos. Los beneficios por unidad, el uso de mano de obra por unidad, la demanda mensual y el uso por unidad de tiempo de máquina se muestran en la tabla siguiente:
Ratones
Teclados
Joysticks
Beneficio/unidad
$8
$11
$9
Uso/unidad de mano de obra
hora .2
0,3 horas
.24 horas
Tiempo/unidad de la máquina
hora .04
0,055 horas
hora .04
Demanda mensual
15 000
27,000
11,000
-
Cada mes, hay disponibles un total de 13.000 horas de trabajo y 3.000 horas de tiempo de máquina. ¿Cómo puede el fabricante maximizar su contribución mensual a los beneficios de la planta?
-
Resuelva nuestro ejemplo de drogas suponiendo que se debe satisfacer una demanda mínima de 200 unidades para cada medicamento.
-
Jason hace pulseras de diamantes, collares y pendientes. Quiere trabajar un máximo de 160 horas al mes. Tiene 800 onzas de diamantes. A continuación se indican los beneficios, el tiempo de trabajo y las onzas de diamantes necesarios para producir cada producto. Si la demanda de cada producto es ilimitada, ¿cómo puede Jason maximizar sus ganancias?
Producto
Ganancias por unidad
Horario laboral por unidad
Onzas de diamantes por unidad
Brazalete
300 $
.35
1,2
Collar
200 $
.15
.75
Pendientes
100 $
0,05
,5







