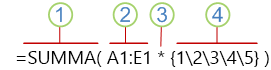Matriisikaavoihin liittyviä ohjeita ja esimerkkejä

Tässä harjoituksessa näet, miten voit käyttää monisoluisia ja yksisoluisia matriisikaavoja myyntilukujen laskemiseen. Ensimmäisessä vaiheessa käytetään monisoluista kaavaa välisummien laskemiseen. Toisessa vaiheessa käytetään yksisoluista kaavaa loppusumman laskemiseen.

• Monisoluinen matriisikaava

  

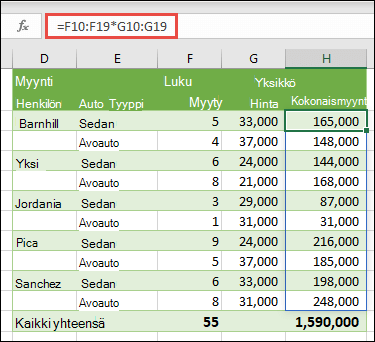
• Tässä laskemme coupe- ja sedan-mallisten autojen kokonaismyynnin kullekin myyjälle kirjoittamalla soluun H10 =F10:F19*G10:G19.

  Kun painat Enter, näet tulosten levittyvän alas soluihin H10:H19. Huomaa, että levittymisalue näkyy korostettuna reunaviivalla, kun valitset minkä tahansa solun levittymisalueelta. Saatat myös huomata, että solujen H10:H19 kaavat näkyvät harmaina. Ne ovat vain viitteenä, joten jos haluat säätää kaavaa, sinun on valittava solu H10, jossa pääkaava sijaitsee.

• Yksisoluinen matriisikaava

  

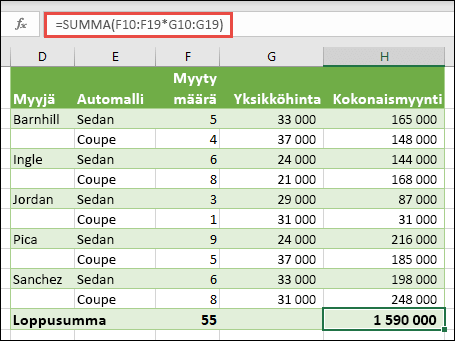
  Kirjoita tai kopioi ja liitä esimerkkityökirjan soluun H20 =SUMMA(F10:F19*G10:G19) ja paina sitten Enter.

  Tässä tapauksessa Excel kertoo matriisin arvot (solualue F10-G19) ja käyttää SUMMA-funktiota summien yhteenlaskemiseen. Kokonaismyynnin tulos on 1 590 000 dollaria.

  Tämä esimerkki osoittaa, miten tehokas matriisikaava voi olla. Oletetaan esimerkiksi, että taulukossa on 1 000 riviä tietoja. Voit laskea yhteen osan tiedoista tai kaikki tiedot luomalla yksisoluisen matriisikaavan sen sijaan, että vetäisit kaavan kaikkiin 1 000 riviin. Huomaa myös, että yksisoluinen kaava solussa H20 on täysin riippumaton monisoluisesta kaavasta (kaava soluissa H10–H19). Tämä joustavuus on yksi matriisikaavojen käytön eduista. Voit muuttaa sarakkeen H muita kaavoja vaikuttamatta kaavaan H20:ssä. Voi myös olla hyvä käytäntö, että sinulla on tällaisia itsenäisiä yhteissummia, sillä se auttaa varmistamaan tulosten tarkkuuden.

• Muita dynaamisten matriisikaavojen etuja ovat:

  • Yhdenmukaisuus    Jos valitset minkä tahansa solun solusta H10 alaspäin, näet saman kaavan. Yhdenmukaisuus auttaa varmistamaan tietojen tarkkuuden.

  • Turvallisuus    Et voi korvata monisoluisen matriisikaavan osaa. Napsauta esimerkiksi solua H11 ja paina Poista. Excel ei muuta matriisin tulosta. Jos haluat muuttaa sitä, sinun on valittava taulukon vasemmassa yläkulmassa oleva solu tai solu H10.

  • Entistä pienemmät tiedostot    You can often use a single array formula instead of several intermediate formulas. Esimerkiksi autokaupan esimerkissä lasketaan tulokset sarakkeessa E yhdellä matriisikaavalla. Jos olisit käyttänyt vakiokaavoja (kuten =F10*G10, F11*G11, F12*G12 jne.), olisit käyttänyt 11 erilaista kaavaa samojen tulosten laskemiseen. Se ei ole iso juttu, mutta entä jos sinulla olisi tuhansia yhteenlaskettavia rivejä? Silloin sillä voi olla suuri merkitys.

  • Tehokkuus    Matriisifunktiot voivat olla tehokas tapa luoda monimutkaisia kaavoja. Matriisikaava =SUMMA(F10:F19*G10:G19) on sama kuin tämä: =SUMMA(F10*G10,F11*G11,F12*G12,F13*G13,F14*G14,F15*G15,F16*G16,F17*G17,F18*G18,F19*G19).

  • Levittyminen    Dynaamiset matriisikaavat levittyvät automaattisesti tulostusalueelle. Jos lähdetiedot ovat Excel-taulukossa, dynaamiset matriisikaavat muuttavat kokoa automaattisesti, kun lisäät tai poistat tietoja.

  • #SPILL!-virhe    Dynaamiset matriisit tuottavat #SPILL!-virheen, mikä tarkoittaa, että aiottu levittymisalue on jostain syystä estetty. Kun poistat eston, kaava levittyy automaattisesti.

Taulukon vakiot ovat osa matriisikaavoja. Matriisivakioita voi luoda määrittämällä kohdeluettelo ja lisäämällä luettelon ympärille aaltosulkeet ({ }), esimerkiksi näin:

={1\2\3\4\5} tai ={"tammikuu"\"helmikuu"\"maaliskuu"}

Jos erotat kohteet toisistaan pilkkujen avulla, luot vaakasuuntaisen matriisin (rivi). Jos erotat kohteet toisistaan puolipisteiden avulla, luot pystysuuntaisen matriisin (sarake). Jos haluat luoda kaksiulotteisen matriisin, erota kunkin rivin kohteet toisistaan pilkuilla ja erota rivit toisistaan puolipisteillä.

Seuraavien toimien avulla voit harjoitella vaaka- ja pystysuuntaisten sekä kaksiulotteisten vakioiden luomista. Näytämme esimerkkejä, joissa käytetään SEQUENCE-funktiota matriisivakioiden luomiseen automaattisesti sekä manuaalisesti kirjoitettuja matriisivakioita.

• Vaakasuuntaisen vakion luominen

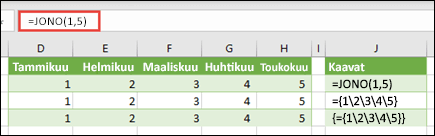
  Käytä edellisessä kohdassa käytettyä työkirjaa tai avaa uusi työkirja. Valitse mikä tahansa tyhjä solu ja kirjoita =JONO(1,5). SEQUENCE-funktio muodostaa 1 rivin ja 5 sarakkeen matriisin samalla tavalla kuin ={1\2\3\4\5}. Näet seuraavat tulokset:

  

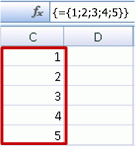
• Pystysuuntaisen vakion luominen

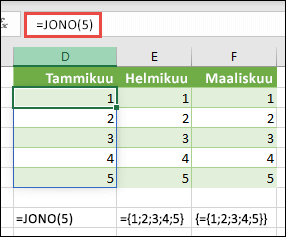
  Valitse mikä tahansa tyhjä solu, jonka alapuolella on tilaa, ja kirjoita =JONO(5) tai ={1;2;3;4;5}. Näet seuraavat tulokset:

  

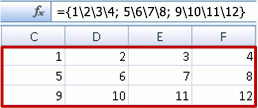
• Kaksiulotteisen vakion luominen

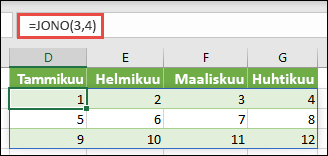
  Valitse mikä tahansa tyhjä solu, jonka oikealla ja alapuolella on tilaa, ja kirjoita =JONO(3,4). Näet seuraavat tulokset:

  

  Voit myös kirjoittaa: tai ={1\2\3\4;5\6\7\8;9\10\11\12}, mutta kiinnitä huomiota kohtaan, johon laitat puolipisteet pilkkujen sijaan.

  Kuten näet, JONO-vaihtoehto tarjoaa merkittäviä etuja matriisivakioarvojen manuaaliseen syöttämiseen verrattuna. Ensisijaisesti se säästää aikaa, mutta se voi myös auttaa vähentämään manuaalisen syöttämisen virheitä. Se on myös helpompi lukea, etenkin kun puolipisteitä voi olla vaikea erottaa pilkuista.

Seuraavassa esimerkissä käytetään matriisivakioita osana suurempaa kaavaa. Siirry mallityökirjassa Vakio kaavassa laskentataulukkoon tai luo uusi laskentataulukko.

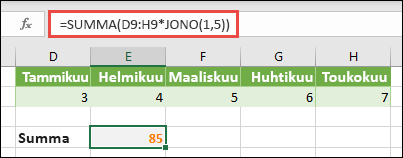
Kirjoitimme soluun D9 =JONO(1,5,3,1), mutta voit kirjoittaa soluihin A9:H9 myös 3, 4, 5, 6 ja 7. Tässä numerovalinnassa ei ole mitään erityistä. Valitsimme vain välillä jonkin muun kuin 1-5.

Kirjoita soluun E11 =SUMMA(D9:H9*JONO(1,5))tai =SUMMA(D9:H9*{1\2\3\4\5}). Kaavat palauttavat arvon 85.

JONO-funktio muodostaa matriisivakiota {1\2\3\4\5} vastaavan arvon. Koska Excel suorittaa ensin sulkeissa olevat lausekkeet, seuraavat kaksi osaa ovat solujen arvot kohdassa D9:H9 sekä kerroinoperaattori (*). Tässä vaiheessa kaava kertoo tallennetun matriisin arvot vakion vastaavilla arvoilla. Tämä vaihe vastaa kaavaa:

=SUMMA(D9*1,E9*2,F9*3,G9*4,H9*5) tai =SUMMA(3*1,4*2,5*3,6*4,7*5)

Lopuksi SUMMA-funktio lisää arvot ja palauttaa 85.

Voit välttää tallennetun matriisin käyttämisen ja säilyttää operaattorin muistissa korvaamalla sen toisella matriisivakiolla:

=SUMMA(JONO(1,5,3,1)*JONO(1,5)) tai =SUMMA({3\4\5\6\7}*{1\2\3\4\5})

Matriisivakioissa käytettävät osat

• Matriisivakiot voivat sisältää numeroita, tekstiä, totuusarvoja (kuten TOSI ja EPÄTOSI) ja virhearvoja, kuten #N/A. Voit käyttää lukuja kokonaisluku-, desimaali- ja tieteellisissä muodoissa. Jos käytät vakiossa tekstiä, sen ympärille on lisättävä lainausmerkit (“teksti”).

• Matriisivakiot eivät voi sisältää muita matriiseja, kaavoja tai funktioita. Toisin sanoen ne voivat sisältää vain pilkuilla tai puolipisteillä erotettuja numeroita tai tekstejä. Excel näyttää varoitussanoman, jos kirjoitat esimerkiksi kaavan {1\2\A1:D4} tai {1\2\SUMMA(Q2:Z8)}. Numeeriset arvot eivät voi sisältää prosenttimerkkejä, dollarin merkkejä, pilkkuja tai sulkeita.

Yksi parhaista tavoista käyttää matriisivakioita on nimetä ne. Nimettyjä vakioita on helppo käyttää, ja niiden avulla matriisikaavoista voidaan tehdä helpommin ymmärrettäviä muille käyttäjille. Voit nimetä matriisivakion ja käyttää sitä kaavassa seuraavalla tavalla:

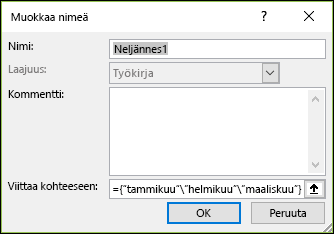
Valitse Kaavat > Määritetyt nimet > Määritä nimi. Kirjoita Nimi-ruutuun Neljännes1. Kirjoita Viittaa-ruutuun seuraava vakio (muista lisätä aaltosulkeet):

={"tammikuu"\"helmikuu"\"maaliskuu"}

Valintaikkunan pitäisi nyt näyttää tältä:

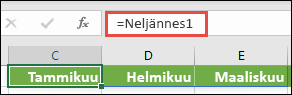
Valitse OK, ja valitse sitten mikä tahansa rivi, jossa on kolme tyhjää solua, ja kirjoita =Neljännes1.

Näet seuraavat tulokset:

Jos haluat tulosten levittyvän pystysuunnassa vaakasuuntaisen sijaan, voit käyttää =TRANSPONOI(Vuosineljännes1).

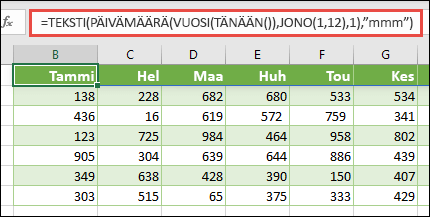
Jos haluat näyttää 12 kuukauden luettelon, jollaista saatat käyttää laatiessasi talousraporttia, voit luoda JONO-funktiolla sellaisen kuluvasta vuodesta. Hienoa tässä funktiossa on se, että vaikka vain kuukausi on näkyvissä, sen takana on kelvollinen päivämäärä, jota voit käyttää muissa laskutoimituksissa. Nämä esimerkit löytyvät esimerkkityökirjan taulukoista Nimetty matriisivakioja Nopea näytetietojoukko.

=TEKSTI(PÄIVÄYS(VUOSI(TÄMÄ.PÄIVÄ()),JONO(1,12),1),"mmm")

Tämä käyttää PÄIVÄYS-funktiota luomaan päivämäärän kuluvan vuoden perusteella, JONO luo matriisivakion 1-12 tammikuusta joulukuuhun ja sitten TEKSTI-funktio muuntaa näyttömuodon muotoon "mmm" (tam, hel, maa jne.). Jos haluat näyttää koko kuukauden nimen, kuten tammikuu, käytä "mmmm".

Kun käytät nimettyä vakiota matriisikaavana, muista lisätä yhtäläisyysmerkki, kuten =Neljännes1, ei ainoastaan Neljännes1. Jos et lisää yhtäläisyysmerkkiä, Excel tulkitsee matriisin tekstimerkkijonoksi eikä kaava toimi odotetulla tavalla. Muista myös, että voit käyttää funktioiden, tekstin ja numeroiden yhdistelmiä. Kaikki riippuu siitä, kuinka luova haluat olla.

Seuraavissa esimerkeissä esitellään muutamia matriisivakioiden käyttötapoja matriisikaavoissa. Muutamissa esimerkeissä käytetään TRANSPONOI-funktiota, joka muuttaa rivit sarakkeiksi ja päinvastoin.

• Matriisin kunkin kohteen kertominen

  Kirjoita =JONO(1,12)*2 tai ={1\2\3\4;5\6\7\8;9\10\11\12}*2

  Voit myös jakaa (/), lisätä (+) ja vähentää (-).

• Matriisin kohteiden neliöjuuri

  Kirjoita =JONO(1,12)^2 tai ={1\2\3\4;5\6\7\8;9\10\11\12}^2

• Etsi neliökohteiden neliöjuuri matriisista

  Kirjoita =NELIÖJUURI(JONO(1,12)^2)tai =NELIÖJUURI({1\2\3\4;5\6\7\8;9\10\11\12}^2)

• Yksiulotteisen rivin transponoiminen

  Kirjoita =TRANSPONOI(JONO(1,5)) tai =TRANSPONOI({1,2,3,4,5})

  Vaikka olet määrittänyt vaakasuuntaisen matriisivakion, TRANSPONOI-funktio muuntaa matriisivakion sarakkeeksi.

• Yksiulotteisen sarakkeen transponoiminen

  Kirjoita =TRANSPONOI(JONO(5,1)) tai =TRANSPONOI({1;2;3;4;5})

  Vaikka olet määrittänyt pystysuuntaisen matriisivakion, TRANSPONOI-funktio muuntaa matriisivakion riviksi.

• Kaksiulotteisen vakion transponoiminen

  Kirjoita =TRANSPONOI(JONO(3,4)) tai =TRANSPONOI({1\2\3\4;5\6\7\8;9\10\11\12})

  TRANSPONOI-funktio muuntaa kunkin rivin sarakejoukoksi.

Tässä osassa on esimerkkejä perusmatriisikaavoista.

• Matriisin luominen olemassa olevista arvoista

  Seuraavassa esimerkissä kerrotaan, miten matriisikaavojen avulla luodaan uusi matriisi olemassa olevasta matriisista.

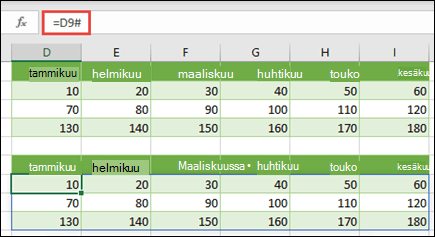
  Kirjoita =JONO(3,6,10,10) tai ={10\20\30\40\50\60;70\80\90\100\110\120;130\140\150\160\170\180}

  Muista kirjoittaa { (aloittava aaltosulje) ennen lukua 10 ja } (päättävä aaltosulje) luvun 180 jälkeen, sillä luot lukumatriisia.

  Kirjoita seuraavaksi =D9# tai =D9:I11 tyhjään soluun. Näkyviin tulee 3 x 6 solutaulukko, jossa on samat arvot kuin soluissa D9:D11. #-merkkiä kutsutaan levittyneen alueen operaattoriksi, ja se on Excelin tapa viitata koko matriisialueeseen sen sijaan, että se olisi kirjoitettava.

  

• Matriisivakion luominen olemassa olevista arvoista

  Voit ottaa levittyneen matriisikaavan tulokset ja muuntaa ne sen komponenttiosiksi. Valitse solu D9 ja siirry sitten muokkaustilaan painamalla F2. Seuraavaksi muunna soluviittaukset arvoiksi painamalla F9-näppäintä. Excel muuntaa arvot matriisivakioksi. Kun painat Enter, kaavan =D9# pitäisi nyt olla ={10\20\30;40\50\60;70\80\90}.

• Solualueen merkkimäärän laskeminen

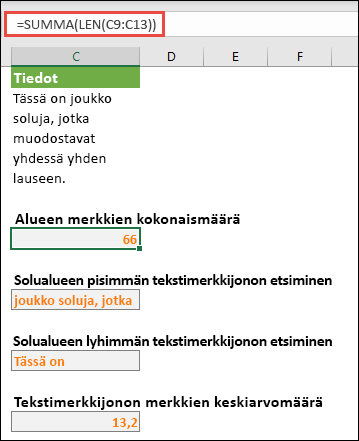
  Seuraavassa esimerkissä kerrotaan, miten voit laskea solualueen merkkien määrän. Tämä sisältää välilyönnit.

  

  =SUMMA(PITUUS(C9:C13))

  Tässä tapauksessa PITUUS-funktio palauttaa kunkin tekstimerkkijonon pituuden kussakin alueen solussa. SUMMA-funktio laskee arvot yhteen ja näyttää tuloksen (66). Jos haluat saada merkkien keskimääräisen määrän, voit käyttää seuraavia:

  =KESKIARVO(PITUUS(C9:C13))

• Alueen C9:C13 pisimmän solun sisältö

  =INDEKSI(C9:C13,VASTINE(MAKS(PITUUS(C9:C13)),PITUUS(C9:C13),0),1)

  Tämä kaava toimii vain, kun tietoalue sisältää yhden solusarakkeen.

  Tutkitaanpa kaavaa hieman tarkemmin sisimmäisistä osista alkaen. PITUUS-funktio palauttaa kunkin solualueen D2:D6 kohteen pituuden. MAKS-funktio laskee kohteiden suurimman arvon, joka vastaa pisintä merkkijonoa, joka on solussa D3.

  Tässä vaiheessa asia muuttuu hieman monimutkaisemmaksi. VASTINE-funktio laskee sen solun siirtymän (suhteellisen sijainnin), joka sisältää pisimmän tekstimerkkijonon. Funktio tarvitsee laskemisessa kolmea argumenttia hakuarvo, hakumatriisi sekä vastinetyyppi. VASTINE-funktio etsii hakumatriisin määritetylle hakuarvolle. Tässä tapauksessa hakuarvo on pisin tekstimerkkijono:

  MAKS(PITUUS(C9:C13)

  ja merkkijono sijaitsee tässä matriisissa:

  PITUUS(C9:C13)

  Tässä tapauksessa vastinetyyppiargumentti on 0. Vastinetyypin arvo voi olla 1, 0 tai -1.

  • 1 - palauttaa suurimman arvon, joka on pienempi tai yhtä suuri kuin hakuarvo

  • 0 - palauttaa ensimmäisen arvon, joka on täsmälleen yhtä suuri kuin hakuarvo

  • -1 - palauttaa pienimmän arvon, joka on suurempi tai yhtä suuri kuin määritetty hakuarvo

  • Jos et määritä vastinetyyppiä, Excel käyttää oletusarvoa 1.

  Lopuksi INDEKSI-funktio ottaa nämä argumentit: matriisi sekä rivin ja sarakkeen numero siinä matriisissa. Solualue C9:C13 antaa matriisin, VASTINE-funktio antaa solun osoitteen ja viimeinen argumentti (1) määrittää, että arvo tulee matriisin ensimmäisestä sarakkeesta.

  Jos haluat saada pienimmän tekstimerkkijonon sisällön, korvaa MAKS yllä olevassa esimerkissä funktiolla MIN.

• Alueen n:n pienimmän arvon etsiminen

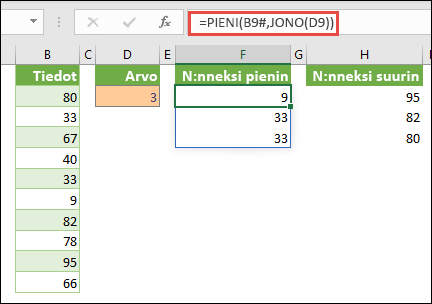
  Tässä esimerkissä näytetään, miten löydät kolme pienintä arvoa solualueelta, jossa on luotu esimerkkitietojen matriisi soluissa B9:B18 seuraavasti: =KOKONAISLUKU(SATUNN.MATRIISI(10,1)*100). Huomaa, että SATUNN.MATRIISI on muuttuva funktio, joten saat uuden joukon satunnaislukuja aina, kun Excel laskee.

  

  Kirjoita =PIENI(B9#,JONO(D9), =PIENI(B9:B18,{1;2;3})

  Tämä kaava käyttää matriisivakiota PIENI-funktion arvioimiseen kolme kertaa ja palauttaa pienimmät kolme jäsentä matriisissa, joka sisältyy soluihin B9:B18, jossa 3 on muuttuja-arvo solussa D9. Jos haluat etsiä lisää arvoja, voit suurentaa JONO-funktion arvoa tai lisätä vakioon argumentteja. Voit käyttää tämän kaavan kanssa myös muita funktioita, kuten SUMMA- tai KESKIARVO-funktioita. Esimerkki:

  =SUMMA(PIENI(B9#,JONO(D9))

  =KESKIARVO(PIENI(B9#,JONO(D9))

• Alueen n:n suurimman arvon etsiminen

  Jos haluat etsiä alueen suurimmat arvot, korvaa PIENI-funktio SUURI-funktiolla. Seuraavassa esimerkissä käytetään lisäksi RIVI- ja EPÄSUORA-funktioita.

  Kirjoita =SUURI(B9#,RIVI(EPÄSUORA("1:3")))tai =SUURI(B9:B18,RIVI(EPÄSUORA("1:3")))

  Tässä vaiheessa voi olla hyödyllistä tietää hieman RIVI- ja EPÄSUORA-funktioista. RIVI-funktiolla voit luoda joukon peräkkäisiä kokonaislukuja. Valitse esimerkiksi tyhjä ja kirjoita:

  =RIVI(1:10)

  Kaava luo kymmenen peräkkäisen kokonaisluvun sarakkeen. Jos haluat tarkastella mahdollisia ongelmia, lisää rivi matriisikaavan sisältävän alueen yläpuolelle (eli rivin 1 yläpuolelle). Excel tarkistaa riviviittaukset ja kaava luo nyt kokonaisluvut 2-11. Voit korjata ongelman lisäämällä kaavaan EPÄSUORA-funktion:

  =RIVI(EPÄSUORA("1:10"))

  EPÄSUORA-funktio käyttää tekstimerkkijonoja argumentteina (tästä syystä alueen 1:10 ympärillä on lainausmerkit). Excel ei muuta tekstiarvoja, kun lisäät rivejä tai siirrät matriisikaavaa. Funktion ansiosta RIVI-funktio luo aina matriisin ainoastaan haluamistasi kokonaisluvuista. Voit yhtä helposti käyttää JONO-funktiota:

  =JONO(10)

  Tarkastellaan aiemmin käyttämääsi kaavaa — =SUURI(B9#,RIVI(EPÄSUORA("1: 3"))) — alkaen sisemmistä sulkeista ja siirtymällä ulospäin: EPÄSUORA-funktio palauttaa joukon tekstiarvoja, tässä tapauksessa arvot 1-3. RIVI-funktio puolestaan ​​luo kolmen solun sarakematriisin. SUURI-funktio käyttää arvoja solualueella B9:B18, ja se arvioidaan kolme kertaa, kerran kutakin RIVI-funktion palauttamaa vertailua kohti. Jos haluat löytää enemmän arvoja, lisää EPÄSUORA-funktioon suurempi solualue. Kuten PIENI-esimerkeissä, voit käyttää tätä kaavaa myös muiden funktioiden, kuten SUMMA- ja KESKIARVO-funktioiden, kanssa.

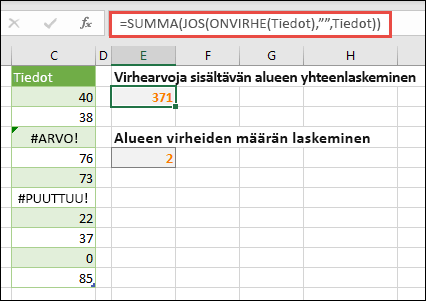
• Virhearvoja sisältävän alueen yhteenlaskeminen

  Excelin SUMMA-funktio ei toimi, jos yrität laskea yhteen alueen, joka sisältää virhearvon, kuten #ARVO! tai #N/A. Tässä esimerkissä näytetään, miten voit laskea yhteen Tiedot-nimisen alueen, joka sisältää virheitä:

  

• =SUMMA(JOS(ONVIRHE(Tiedot);"";Tiedot))

  Kaava luo uuden taulukon, joka sisältää alkuperäiset arvot lukuun ottamatta virhearvoja. Sisemmistä funktioista alkaen ja ulospäin siirtymällä ONVIRHE-funktio etsii solualueelta (Data) virheitä. JOS-funktio palauttaa tietyn arvon, jos määrittämäsi ehto arvioi arvoksi TOSI ja toisen arvon, jos se arvioi arvoksi EPÄTOSI. In this case, it returns empty strings ("") for all error values because they evaluate to TRUE, and it returns the remaining values from the range (Data) because they evaluate to FALSE, meaning that they don't contain error values. SUMMA-funktio laskee sitten suodatetun matriisin kokonaissumman.

• Alueen virhearvojen määrän laskeminen

  Tässä esimerkissä käytetään samantyyppistä kaavaa kuin edellisessä esimerkissä, mutta kaava palauttaa Tiedot-alueen virhearvojen määrän sen sijaan, että virhearvot suodatettaisiin pois:

  =SUMMA(JOS(ONVIRHE(Tiedot);1;0))

  Tämä kaava luo matriisin, joka sisältää arvon 1 soluille, joissa on virheitä, ja arvon 0 soluille, joissa ei ole virheitä. Voit yksinkertaistaa kaavaa ja saada saman tuloksen poistamalla JOS-funktion kolmannen argumentin:

  =SUMMA(JOS(ONVIRHE(Tiedot);1))

  Jos et määritä argumenttia, JOS-funktio palauttaa arvon EPÄTOSI, jos solu ei sisällä virhearvoa. Voit yksinkertaistaa kaavaa edelleen:

  =SUMMA(JOS(ONVIRHE(Tiedot)*1))

  Tämä kaava toimii, koska TOSI*1=1 ja EPÄTOSI*1=0.

Saatat joutua laskemaan arvot yhteen ehtojen perusteella.

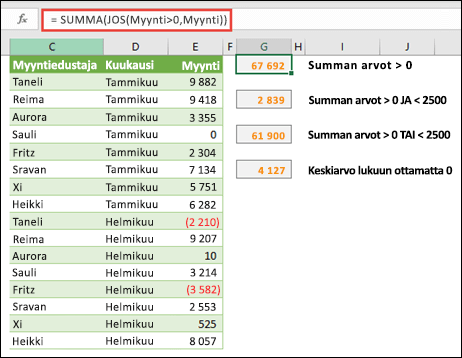
Esimerkiksi seuraava matriisikaava laskee yhteen vain positiiviset kokonaisluvut Myynti-nimisellä alueella, joka on soluissa E9:E24 yllä olevassa esimerkissä:

=SUMMA(JOS(Myynti>0,Myynti))

JOS-funktio luo positiivisten ja epätosien arvojen matriisin. SUMMA-funktio ohittaa virheelliset arvot, koska 0+0=0. Kaavassa käytettävä solualue voi sisältää haluamasi määrän rivejä ja sarakkeita.

Voit myös laskea yhteen arvot, jotka vastaavat useampaa kuin yhtä ehtoa. Esimerkiksi tämä matriisikaava laskee arvot, jotka ovat suurempia kuin 0 JA pienempiä kuin 2 500:

=SUMMA((Myynti>0)*(Myynti<2500)*(Myynti))

Huomaa, että tämä kaava palauttaa virheen, jos alue sisältää ei-numeerisia soluja.

Voit myös luoda matriisikaavoja, jotka käyttävät TAI-ehtoa. Voit esimerkiksi laskea yhteen arvot, jotka ovat suurempia kuin 0 TAI pienempiä kuin 2 500:

=SUMMA(JOS((Myynti>0)+(Myynti<2500),Myynti))

Matriisikaavoissa ei voi käyttää suoraan JA- ja TAI-funktioita, koska nämä funktiot palauttavat yksittäisen tuloksen (joko TOSI tai EPÄTOSI) ja matriisifunktiot edellyttävät tulosmatriiseja. Voit kiertää ongelman käyttämällä edellisessä kaavassa esitettyä logiikkaa. Toisin sanoen suoritat matemaattisia operaatioita, kuten lisäys tai kertolasku arvoille, jotka täyttävät TAI- tai JA-ehdon.

Tässä esimerkissä näytetään, miten voit poistaa nollat alueelta, kun haluat laskea alueen arvojen keskiarvon. Kaavassa käytetään Myynti-nimistä tietoaluetta:

=KESKIARVO(JOS(Myynti<>0;Myynti))

JOS-funktio luo matriisin arvoista, jotka ovat eri suuria kuin 0, ja siirtää arvot sitten KESKIARVO-funktiolle.

This array formula compares the values in two ranges of cells named MyData and YourData and returns the number of differences between the two. If the contents of the two ranges are identical, the formula returns 0. Tämän kaavan käyttämiseksi solualueiden on oltava samankokoisia ja samasta dimensiosta. Jos esimerkiksi MyData on kolmen rivin ja viiden sarakkeen alue, YourDatan on oltava myös kolme riviä ja viisi saraketta:

=SUMMA(JOS(MyData=YourData,0,1))

Kaava luo uuden matriisin, joka on samankokoinen kuin vertailtavat alueet. JOS-funktio lisää matriisiin arvon 0 ja arvon 1 (0 tarkoittaa eroavaisuuksia ja 1 identtisiä soluja). SUMMA-funktio palauttaa matriisin arvojen summan.

Voit yksinkertaistaa kaavaa seuraavasti:

=SUMMA(1*(MyData<>YourData))

Tämä kaava toimii samalla tavalla kuin alueen virhearvoja laskeva kaava, koska TOSI*1=1 ja EPÄTOSI*1=0.

Tämä matriisikaava palauttaa yksisarakkeisen Tiedot-nimisen alueen suurimman arvon rivinumeron:

=MIN(JOS(Tiedot=MAKS(Tiedot);RIVI(Tiedot);""))

JOS-funktio luo uuden matriisin, joka vastaa Tiedot-aluetta. Jos solu sisältää alueen suurimman arvon, matriisissa on rivinumero. Muissa tapauksissa matriisi sisältää tyhjän merkkijonon (""). MIN-funktio käyttää uutta matriisia toisena argumenttinaan ja palauttaa pienimmän arvon, joka vastaa Tiedot-alueen suurimman arvon rivinumeroa. Jos Tiedot-alueella on useita täysin samanlaisia suurimpia arvoja, kaava palauttaa ensimmäisen arvon rivinumeron.

Jos haluat selvittää suurimman arvon todellisen solun osoitteen, käytä seuraavaa kaavaa:

=OSOITE(MIN(JOS(Tiedot=MAKS(Tiedot);RIVI(Tiedot);""));SARAKE(Tiedot))

Samankaltaisia esimerkkejä on esimerkkityökirjan Tietojoukkojen väliset erot -laskentataulukossa.

Tässä harjoituksessa näet, miten voit käyttää monisoluisia ja yksisoluisia matriisikaavoja myyntilukujen laskemiseen. Ensimmäisessä vaiheessa käytetään monisoluista kaavaa välisummien laskemiseen. Toisessa vaiheessa käytetään yksisoluista kaavaa loppusumman laskemiseen.

• Monisoluinen matriisikaava

Kopioi koko alla oleva taulukko ja liitä se tyhjän taulukon soluun A1.

Myynti henkilö	Auto tyyppi	Myynti määrä	Yksikkö hinta	Kokonais myynti
Barnhill	Sedan	5	33000
	Coupe	4	37000
Ingle	Sedan	6	24000
	Coupe	8	21000
Jordania	Sedan	3	29000
	Coupe	1	31000
Pica	Sedan	9	24000
	Coupe	5	37000
Sanchez	Sedan	6	33000
	Coupe	8	31000
Kaava (loppusumma)			Loppusumma
'=SUMMA(C2:C11*D2:D11)			=SUMMA(C2:C11*D2:D11)

1. Jos haluat nähdä kunkin myyjän coupe- ja sedan-kokonaismyynnin, valitse solut E2:E11, kirjoita kaava =C2:C11*D2:D11ja paina sitten näppäinyhdistelmää Ctrl+Vaihto+Enter.

2. Saat kaikkien myytyjen autojen loppusumman valitsemalla solun F11, kirjoittamalla kaavan =SUMMA(C2:C11*D2:D11) ja painamalla näppäinyhdistelmää Ctrl+Vaihto+Enter.

Kun painat Ctrl+Vaihto+Enter, Excel ympäröi kaavan aaltosulkeilla ({ }) ja lisää kaavan esiintymän valitun alueen kuhunkin soluun. Kaavan lisääminen tapahtuu nopeasti, ja sarakkeessa E näkyy kunkin automallin kokonaismyyntimäärä myyjittäin. Jos valitset ensin E2, sitten E3, E4 ja niin edelleen, huomaat, että käytössä on koko ajan sama kaava: {=C2:C11*D2:D11}. 

• Yksisoluisen matriisikaavan luominen

Kirjoita työkirjan soluun D13 seuraava kaava ja paina näppäinyhdistelmää Ctrl+Vaihto+Enter:

=SUMMA(C2:C11*D2:D11)

Tässä tapauksessa Excel kertoo matriisin arvot (solualue C2-D11) ja käyttää SUMMA-funktiota summien yhteenlaskemiseen. Kokonaismyynnin tulos on 1 590 000 dollaria. Tämä esimerkki osoittaa, miten tehokas matriisikaava voi olla. Oletetaan esimerkiksi, että taulukossa on 1 000 riviä tietoja. Voit laskea yhteen osan tiedoista tai kaikki tiedot luomalla yksisoluisen matriisikaavan sen sijaan, että vetäisit kaavan kaikkiin 1 000 riviin.

Huomaa myös, että yksisoluinen kaava (solussa D13) on täysin riippumaton monisoluisesta kaavasta (kaava soluissa E2–E11). Tämä joustavuus on yksi matriisikaavojen käytön eduista. Voit muuttaa sarakkeessa E olevia kaavoja tai poistaa koko sarakkeen ilman, että solun D13 kaavassa tapahtuu muutoksia.

Muita matriisikaavojen etuja ovat:

• Yhdenmukaisuus    Jos valitset minkä tahansa solun solusta E2 alaspäin, näet saman kaavan. Yhdenmukaisuus auttaa varmistamaan tietojen tarkkuuden.

• Turvallisuus    You cannot overwrite a component of a multi-cell array formula. Valitse esimerkiksi solu E3 ja paina Delete-näppäintä. You have to either select the entire range of cells (E2 through E11) and change the formula for the entire array, or leave the array as is. Turvallisuussyistä sinun on vahvistettava kaavaan tehdyt muutokset painamalla näppäinyhdistelmää Ctrl+Vaihto+Enter.

• Entistä pienemmät tiedostot    You can often use a single array formula instead of several intermediate formulas. Esimerkiksi työkirjassa lasketaan tulokset sarakkeessa E yhdellä matriisikaavalla. Jos olisit käyttänyt vakiokaavoja (kuten =C2*D2, C3*D3, C4*D4...), olisit käyttänyt 11 erilaista kaavaa samojen tulosten laskemiseen.

Yleensä matriisikaavoissa käytetään vakiokaavan syntaksia. Matriisikaavan alussa on aina yhtäläisyysmerkki (=), ja matriisikaavoissa voi käyttää useimpia valmiita Excel-funktiota. Tärkein ero on se, että matriisikaavaa käytettäessä kaava kirjoitetaan painamalla Ctrl+Vaihto+Enter. Kun teet tämän, Excel ympäröi matriisikaavasi aaltosulkeilla - jos kirjoitat aaltosulkeet manuaalisesti, kaava muunnetaan tekstimerkkijonoksi, eikä se toimi.

Matriisifunktiot voivat olla tehokas tapa luoda monimutkaisia kaavoja. Matriisikaava =SUMMA(C2:C11*D2:D11) vastaa kaavaa =SUMMA(C2*D2;C3*D3;C4*D4;C5*D5;C6*D6;C7*D7;C8*D8;C9*D9;C10*D10;C11*D11).

Muista monisoluisia kaavoja käsiteltäessä seuraavat seikat:

• Solualue on valittava ennen kaavan kirjoittamista. Harjoittelit tätä monisoluisen matriisikaavan luonnin yhteydessä, kun valitsit solut E2–E11.

• Yksittäisen solun sisältöä ei voi muuttaa matriisikaavassa. Yritä muuttaa solun sisältöä valitsemalla työkirjan solu E3 ja painamalla Delete-näppäintä. Excelissä avautuu sanoma, joka ilmoittaa, että matriisin osaa ei voi muuttaa.

• Voit siirtää tai poistaa kokonaisen matriisikaavan, mutta et voi siirtää tai poistaa osaa siitä. Toisin sanoen, jos haluat lyhentää matriisikaavaa, sinun on ensin poistettava aiemmin luotu kaava ja luotava kaava sitten uudelleen.

• Jos haluat poistaa matriisikaavan, valitse koko kaava-alue (esimerkiksi E2:E11) ja paina sitten Delete-näppäintä.

• Monisoluiseen matriisikaavaan ei voi lisätä tyhjiä soluja eikä siitä voi poistaa soluja.

At times, you may need to expand an array formula. Valitse aiemmin luodun matriisialueen ensimmäinen solu ja jatka, kunnes olet valinnut koko alueen, johon haluat laajentaa kaavan. Muokkaa kaavaa painamalla F2 ja vahvista sitten kaava painamalla näppäinyhdistelmää CTRL+VAIHTO+ENTER, kun olet säätänyt kaava-aluetta. Tärkeintä on valita koko alue alkaen matriisin vasemmasta yläkulmasta. Vasemmassa yläkulmassa oleva solu on se solu, jota muokataan.

Matriisikaavat ovat todella käteviä, mutta niiden käyttämiseen liittyy myös tiettyjä haittapuolia:

• Saatat unohtaa painaa näppäinyhdistelmää Ctrl+Vaihto+Enter. Myös kokeneet Excel-käyttäjät voivat tehdä tämän virheen. Muista painaa tätä näppäinyhdistelmää aina, kun kirjoitat matriisikaavan tai muokkaat sitä.

• Muut työkirjan käyttäjät eivät ehkä ymmärrä kaavojasi. Käytännössä matriisikaavoja ei yleensä selitetä laskentataulukossa. Jos muiden käyttäjien on muokattava työkirjojasi, vältä matriisikaavoja tai varmista, että kyseiset henkilöt tietävät matriisikaavoista ja ymmärtävät, miten niitä voi tarvittaessa muuttaa.

• Suuret matriisikaavat saattavat hidastaa laskutoimituksia tietokoneen käsittelynopeuden ja muistin määrän mukaan.

Matriisivakiot ovat matriisikaavojen osia. Matriisivakioita voi luoda määrittämällä kohdeluettelo ja lisäämällä luettelon ympärille aaltosulkeet ({ }), esimerkiksi

={1\2\3\4\5}

Tässä vaiheessa tiedät jo, että matriisikaavoja luotaessa on painettava näppäinyhdistelmää Ctrl+Vaihto+Enter. Koska matriisivakiot ovat matriisikaavojen osia, vakioiden ympärille lisätään aaltosulkeet manuaalisesti kirjoittamalla. Tämän jälkeen näppäinyhdistelmää Ctrl+Vaihto+Enter käytetään koko kaavan kirjoittamiseen.

Jos erotat kohteet toisistaan pilkkujen avulla, luot vaakasuuntaisen matriisin (rivi). Jos erotat kohteet toisistaan puolipisteiden avulla, luot pystysuuntaisen matriisin (sarake). Jos haluat luoda kaksiulotteisen matriisin, erota kunkin rivin kohteet toisistaan pilkuilla ja erota rivit toisistaan puolipisteillä.

Yhden rivin matriisi: {1\2\3\4}. Yhden sarakkeen matriisi: {1;2;3;4}. Kaksi riviä ja neljä saraketta sisältävä matriisi: {1\2\3\4;5\6\7\8}. Kahden rivin matriisissa ensimmäinen rivi on 1, 2, 3 ja 4 ja toinen rivi on 5, 6, 7 ja 8. Yksi puolipiste erottaa rivit toisistaan 4:n ja 5:n välissä.

Matriisivakiota voi käyttää matriisikaavojen tapaan yhdessä Excelin valmiiden funktioiden kanssa. The following sections explain how to create each kind of constant and how to use these constants with functions in Excel.

Seuraavien toimien avulla voit harjoitella vaaka- ja pystysuuntaisten sekä kaksiulotteisten vakioiden luomista

Vaakasuuntaisen vakion luominen

1. Valitse tyhjässä laskentataulukossa solut A1–E1.

2. Kirjoita kaavariville seuraava kaava ja paina sitten näppäinyhdistelmää Ctrl+Vaihto+Enter:

   ={1\2\3\4\5}

   Tässä tapauksessa sinun pitää kirjoittaa avaavat ja sulkevat aaltosulkeet ({ }), ja Excel lisää toisen joukon puolestasi.

   Näet seuraavat tulokset.

   

Pystysuuntaisen vakion luominen

1. Valitse työkirjassa viiden solun sarake.

2. Kirjoita kaavariville seuraava kaava ja paina sitten näppäinyhdistelmää Ctrl+Vaihto+Enter:

   ={1;2;3;4;5}

   Näet seuraavat tulokset.

   

Kaksiulotteisen vakion luominen

1. Valitse työkirjassa alue, joka on neljä saraketta leveä ja kolme riviä korkea.

2. Kirjoita kaavariville seuraava kaava ja paina sitten näppäinyhdistelmää Ctrl+Vaihto+Enter:

   ={1\2\3\4;5\6\7\8;9\10\11\12}

   Näet seuraavat tulokset:

   

Vakioiden käyttäminen kaavoissa

Tässä yksikertaisessa esimerkissä käytetään vakioita:

1. Luo mallityökirjaan uusi laskentataulukko.

2. Kirjoita 3 soluun A1, 4 soluun B1, 5 soluun C1, 6 soluun D1 ja 7 soluun E1.

3. Kirjoita soluun A3 seuraava kaava ja paina näppäinyhdistelmääCtrl+Vaihto+Enter:

   =SUMMA(A1:E1*{1\2\3\4\5})

   Huomaa, että Excel lisää vakion ympärille toiset aaltosulkeet, koska olet määrittänyt kaavan matriisikaavaksi.

   

   Arvo 85 näkyy solussa A3.

Seuraavassa osassa kerrotaan, miten kaava toimii.

Äsken käyttämäsi kaava sisältää useita osia.

1. Funktio

2. Tallennettu matriisi

3. Kuvaus:

4. Matriisivakio

Viimeinen osa sulkeiden sisäpuolella on matriisivakio: {1\2\3\4\5}. Muista, että Excel ei lisää aaltosulkeita matriisivakioiden ympärille vaan sinun on kirjoitettava ne. Muista myös painaa näppäinyhdistelmää Ctrl+Vaihto+Enter, kun olet lisännyt matriisikaavaan vakion.

Koska Excel suorittaa ensin sulkeissa olevat lausekkeet, seuraavat kaksi osaa ovat työkirjaan tallennetut arvot (A1:E1) sekä operaattori. Tässä vaiheessa kaava kertoo tallennetun matriisin arvot vakion vastaavilla arvoilla. Tämä vaihe vastaa kaavaa:

=SUMMA(A1*1;B1*2;C1*3;D1*4;E1*5)

Lopuksi SUMMA-funktio lisää arvot ja solussa A3 näkyy summa 85.

Voit välttää tallennetun matriisin käyttämisen ja säilyttää operaattorin muistissa korvaamalla tallennetun matriisin toisella matriisivakiolla:

=SUMMA({3\4\5\6\7}*{1\2\3\4\5})

Kokeile tätä kopioimalla funktio, valitsemalla työkirjasta tyhjä solu, liittämällä kaava kaavariville ja painamalla sitten näppäinyhdistelmää Ctrl+Vaihto+Enter. Näet saman tuloksen kuin aiemmassa harjoituksessa, jossa käytettiin matriisikaavaa:

=SUMMA(A1:E1*{1\2\3\4\5})

Array constants can contain numbers, text, logical values (such as TRUE and FALSE), and error values ( such as #N/A). Numeroita voi käyttää kokonaislukuina, desimaalilukuina tai tieteellisinä lukuina. Jos käytät vakiossa tekstiä, tekstin ympärille on lisättävä lainausmerkit (").

Matriisivakiot eivät voi sisältää muita matriiseja, kaavoja tai funktioita. Toisin sanoen ne voivat sisältää vain pilkuilla tai puolipisteillä erotettuja numeroita tai tekstejä. Excel näyttää varoitussanoman, jos kirjoitat esimerkiksi kaavan {1\2\A1:D4} tai {1\2\SUMMA(Q2:Z8)}. Numeeriset arvot eivät voi sisältää prosenttimerkkejä, dollarin merkkejä, pilkkuja tai sulkeita.

Yksi parhaista tavoista käyttää matriisivakioita on nimetä ne. Nimettyjä vakioita on helppo käyttää, ja niiden avulla matriisikaavoista voidaan tehdä helpommin ymmärrettäviä muille käyttäjille. Voit nimetä matriisivakion ja käyttää sitä kaavassa seuraavalla tavalla:

1. Valitse Kaavat-välilehden Määritetyt nimet ryhmästä Määritä nimi.
   Näkyviin tulee Määritä nimi -valintaikkuna.

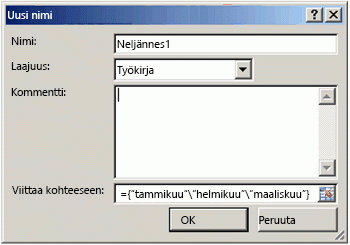
2. Kirjoita Nimi-ruutuun Neljännes1.

3. Kirjoita Viittaa-ruutuun seuraava vakio (muista lisätä aaltosulkeet):

   ={"tammikuu"\"helmikuu"\"maaliskuu"}

   Valintaikkunan sisältö näyttää nyt tältä:

   

4. Valitse ensin OK ja sitten kolmen tyhjän solun rivi.

5. Kirjoita seuraava kaava ja paina näppäinyhdistelmää Ctrl+Vaihto+Enter.

   =Neljännes1

   Näet seuraavat tulokset.

   

Kun käytät nimettyä vakiota matriisikaavana, muista lisätä yhtäläisyysmerkki. Jos et lisää yhtäläisyysmerkkiä, Excel tulkitsee matriisin tekstimerkkijonoksi eikä kaava toimi odotetulla tavalla. Muista myös, että voit käyttää tekstin ja numeroiden yhdistelmiä.

Seuraavat ongelmat saattavat estää matriisivakioiden toimimisen:

• Some elements might not be separated with the proper character. Jos jätät pilkun tai puolipisteen pois tai jos sijoitat sen väärään paikkaan, matriisivakiota ei välttämättä luoda oikein tai näyttöön saattaa tulla varoitussanoma.

• Olet ehkä valinnut solualueen, joka ei vastaa vakion osien määrää. Jos esimerkiksi valitset kuuden solun sarakkeen käytettäväksi yhdessä viisisoluisen vakion kanssa, tyhjässä solussa näkyy virhearvo #PUUTTUU. Conversely, if you select too few cells, Excel omits the values that don't have a corresponding cell.

Seuraavissa esimerkeissä esitellään muutamia matriisivakioiden käyttötapoja matriisikaavoissa. Muutamissa esimerkeissä käytetään TRANSPONOI-funktiota, joka muuttaa rivit sarakkeiksi ja päinvastoin.

Matriisin kunkin kohteen kertominen

1. Luo uusi laskentataulukko ja valitse tyhjä solualue, joka on neljä saraketta leveä ja kolme riviä korkea.

2. Kirjoita seuraava kaava ja paina näppäinyhdistelmää Ctrl+Vaihto+Enter:

   ={1\2\3\4;5\6\7\8;9\10\11\12}*2

Matriisin kohteiden neliöjuuri

1. Valitse tyhjä solualue, joka on neljä saraketta leveä ja kolme riviä korkea.

2. Kirjoita seuraava matriisikaava ja paina näppäinyhdistelmääCtrl+Vaihto+Enter:

   ={1\2\3\4;5\6\7\8;9\10\11\12}*{1\2\3\4;5\6\7\8;9\10\11\12}

   Voit myös kirjoittaa seuraavan matriisikaavan, jossa käytetään sirkumfleksioperaattoria (^):

   ={1\2\3\4;5\6\7\8;9\10\11\12}^2

Yksiulotteisen rivin transponoiminen

1. Valitse viiden tyhjän solun kokoinen sarake.

2. Kirjoita seuraava kaava ja paina näppäinyhdistelmää Ctrl+Vaihto+Enter:

   =TRANSPONOI({1\2\3\4\5})

   Vaikka olet määrittänyt vaakasuuntaisen matriisivakion, TRANSPONOI-funktio muuntaa matriisivakion sarakkeeksi.

Yksiulotteisen sarakkeen transponoiminen

1. Valitse viiden tyhjän solun kokoinen rivi.

2. Kirjoita seuraava kaava ja paina näppäinyhdistelmää Ctrl+Vaihto+Enter:

   =TRANSPONOI({1;2;3;4;5})

Vaikka olet määrittänyt pystysuuntaisen matriisivakion, TRANSPONOI-funktio muuntaa matriisivakion riviksi.

Kaksiulotteisen vakion transponoiminen

1. Valitse solualue, joka on kolme saraketta leveä ja neljä riviä korkea.

2. Kirjoita seuraava vakio ja paina näppäinyhdistelmää Ctrl+Vaihto+Enter:

   =TRANSPONOI({1\2\3\4;5\6\7\8;9\10\11\12})

   TRANSPONOI-funktio muuntaa kunkin rivin sarakejoukoksi.

Tässä osassa on esimerkkejä perusmatriisikaavoista.

Matriisien ja matriisivakioiden luominen olemassa olevista arvoista

Seuraavassa esimerkissä kerrotaan, miten voit luoda yhteyden eri laskentataulukoiden solualueiden välille käyttämällä matriisikaavoja. Esimerkistä käy myös ilmi, miten voi luoda matriisivakion samasta arvojoukosta.

Matriisin luominen olemassa olevista arvoista

1. Valitse Excel-taulukosta solut C8:E10 ja kirjoita tämä kaava:

   ={10\20\30;40\50\60;70\80\90}

   Muista kirjoittaa { (aloittava aaltosulje) ennen lukua 10 ja } (päättävä aaltosulje) luvun 90 jälkeen, sillä luot lukumatriisia.

2. Paina näppäinyhdistelmää Ctrl+Vaihto+Enter, joka syöttää tämän lukumatriisin solualueeseen C8:E10 matriisikaavan avulla. Laskentataulukon solujen C8–E10 pitäisi näyttää tältä:

   10	20	30
   40	50	60
   70	80	90

3. Valitse solualue C1–E3.

4. Kirjoita seuraava kaava kaavariville ja paina sitten näppäinyhdistelmää Ctrl+Vaihto+Enter:

   =C8:E10

   Soluihin C1–E3 tulee näkyviin 3x3-solumatriisi, jossa on samat arvot kuin soluissa C8–E10.

Matriisivakion luominen olemassa olevista arvoista

1. Siirry muokkaustilaan painamalla F2-näppäintä solujen C1:C3 ollessa valittuina. 

2. Muuta soluviittaukset arvoiksi painamalla F9-näppäintä. Excel muuntaa arvot matriisivakioksi. Kaavan pitäisi nyt olla ={10\20\30;40\50\60;70\80\90}.

3. Määritä matriisivakio matriisikaavaksi painamalla näppäinyhdistelmää Ctrl+Vaihto+Enter.

Solualueen merkkimäärän laskeminen

Seuraavassa esimerkissä kerrotaan, miten voit laskea solualueen merkkien määrän (mukaan lukien välilyönnit).

1. Kopioi koko taulukko ja liitä se laskentataulukon soluun A1.

   Tiedot
   Tämä on
   solujoukko, joka
   muodostaa
   yhdistettynä
   yhden lauseen.
   Solujen A2:A6 merkit yhteensä
   =SUMMA(PITUUS(A2:A6))
   Pisimmän solun sisältö (A3)
   =INDEKSI(A2:A6,VASTINE(MAKS(PITUUS(A2:A6)),PITUUS(A2:A6),0),1)

2. Valitse solu A8 ja paina sitten Ctrl+Vaihto+Enter nähdäksesi solujen A2:A6 merkkien kokonaismäärän (66).

3. Valitse solu A10 ja paina sitten Ctrl+Vaihto+Enter nähdäksesi solujen A2:A6 pisimmän solun (solu A3) sisällön.

Seuraava, solussa A8 käytettävä kaava, laskee merkkien kokonaismäärän (66) soluissa A2–A6.

=SUMMA(PITUUS(A2:A6))

Tässä tapauksessa PITUUS-funktio laskee solualueen kunkin solun tekstimerkkijonon pituuden. SUMMA-funktio laskee sitten nämä arvot yhteen ja näyttää tuloksen (66).

Alueen n:n pienimmän arvon etsiminen

Tässä esimerkissä kerrotaan, miten voit etsiä solualueen kolme pienintä arvoa.

1. Kirjoita joitakin satunnaisia lukuja soluihin A1:A11.

2. Valitse solut C1–C3. Tämä solujoukko pitää sisällään matriisikaavan palauttamat tulokset.

3. Kirjoita seuraava kaava ja paina näppäinyhdistelmää Ctrl+Vaihto+Enter:

   =PIENI(A1:A11,{1;2;3})

Tämä kaava käyttää matriisivakiota PIENI-funktion kolminkertaiseen arviointiin ja palauttaa soluihin A1:A10 sisältyvän pienimmän (1), toiseksi pienimmän (2) ja kolmanneksi pienimmän (3) matriisin jäsenen. Jos haluat etsiä lisää arvoja, lisää argumentteja vakioon. Voit käyttää tämän kaavan kanssa myös muita funktioita, kuten SUMMA- tai KESKIARVO-funktioita. Esimerkki:

=SUMMA(PIENI(A1:A10,{1\2\3}))

=KESKIARVO(PIENI(A1:A10,{1\2\3}))

Alueen n:n suurimman arvon etsiminen

Jos haluat etsiä alueen suurimmat arvot, korvaa PIENI-funktio SUURI-funktiolla. Seuraavassa esimerkissä käytetään lisäksi RIVI- ja EPÄSUORA-funktioita.

1. Valitse solut D1–D3.

2. Kirjoita kaavariville tämä kaava ja paina sitten näppäinyhdistelmää Ctrl+Vaihto+Enter:

   =SUURI(A1:A10,RIVI(EPÄSUORA("1:3")))

At this point, it may help to know a bit about the ROW and INDIRECT functions. You can use the ROW function to create an array of consecutive integers. Valitse esimerkiksi tyhjä 10 solun sarake harjoitustyökirjasta, kirjoita tämä matriisikaava ja paina sitten näppäinyhdistelmää Ctrl+Vaihto+Enter:

=RIVI(1:10)

Kaava luo kymmenen peräkkäisen kokonaisluvun sarakkeen. Jos haluat tarkastella mahdollisia ongelmia, lisää rivi matriisikaavan sisältävän alueen yläpuolelle (eli rivin 1 yläpuolelle). Excel tarkistaa riviviittaukset ja kaava luo kokonaisluvut 2–11. Voit korjata ongelman lisäämällä kaavaan EPÄSUORA-funktion:

=RIVI(EPÄSUORA("1:10"))

EPÄSUORA-funktio käyttää tekstimerkkijonoja argumentteina (tästä syystä alueen 1:10 ympärillä on lainausmerkit). Excel ei muuta tekstiarvoja, kun lisäät rivejä tai siirrät matriisikaavaa. Funktion ansiosta RIVI-funktio luo aina matriisin ainoastaan haluamistasi kokonaisluvuista.

Tarkastellaan aiemmin käyttämääsi kaavaa — =SUURI(A5:A14,RIVI(EPÄSUORA("1: 3"))) — alkaen sisemmistä sulkeista ja siirtymällä ulospäin: EPÄSUORA-funktio palauttaa joukon tekstiarvoja, tässä tapauksessa arvot 1-3. RIVI-funktio puolestaan ​​luo kolmen solun sarakematriisin. SUURI-funktio käyttää arvoja solualueella A5:A14, ja se arvioidaan kolme kertaa, kerran kutakin RIVI-funktion palauttamaa vertailua kohti. The values 3200, 2700, and 2000 are returned to the three-cell columnar array. If you want to find more values, you add a greater cell range to the INDIRECT function.

Kuten aikaisemmissa esimerkeissä, voit käyttää tätä kaavaa myös muiden funktioiden, kuten SUMMA- ja KESKIARVO-funktioiden, kanssa.

Solualueen pisimmän tekstimerkkijonon etsiminen

Palaa aiempaan tekstimerkkijonoesimerkkiin, kirjoita seuraava kaava tyhjään soluun ja paina näppäinyhdistelmää Ctrl+Vaihto+Enter:

=INDEKSI(A2:A6,VASTINE(MAKS(PITUUS(A2:A6)),PITUUS(A2:A6),0),1)

Näkyy teksti "bunch of cells that".

Tutkitaanpa kaavaa hieman tarkemmin sisimmäisistä osista alkaen. PITUUS-funktio palauttaa solualueen A2:A6 kunkin kohteen pituuden. MAKS-funktio laskee kyseisten kohteiden suurimman arvon, joka vastaa pisintä merkkijonoa, joka on solussa A3.

Tässä vaiheessa asia muuttuu hieman monimutkaisemmaksi. VASTINE-funktio laskee sen solun siirtymän (suhteellisen sijainnin), joka sisältää pisimmän tekstimerkkijonon. Funktio tarvitsee laskemisessa kolmea argumenttia hakuarvo, hakumatriisi sekä vastinetyyppi. VASTINE-funktio etsii hakumatriisin määritetylle hakuarvolle. Tässä tapauksessa hakuarvo on pisin tekstimerkkijono:

(MAX(LEN(A2:A6))

ja merkkijono sijaitsee tässä matriisissa:

LEN(A2:A6)

Vastinetyyppi on 0. Vastinetyyppi voi muodostua arvosta 1, 0 tai -1. Jos määrität arvon 1, VASTINE-funktio palauttaa suurimman arvon, joka on pienempi tai yhtä suuri kuin hakuarvo. Jos määrität arvon 0, VASTINE-funktio palauttaa ensimmäisen arvon, joka on täsmälleen yhtä suuri kuin hakuarvo. Jos määrität arvon -1, VASTINE-funktio palauttaa pienimmän arvon, joka on suurempi tai yhtä suuri kuin määritetty hakuarvo. Jos et määritä vastinetyyppiä, Excel käyttää oletusarvoa 1.

Finally, the INDEX function takes these arguments: an array, and a row and column number within that array. Solualue A2:A6 antaa matriisin, VASTINE-funktio antaa solun osoitteen ja viimeinen argumentti (1) määrittää, että arvo tulee matriisin ensimmäisestä sarakkeesta.

Tässä osassa on esimerkkejä laajennetuista matriisikaavoista.

Virhearvoja sisältävän alueen yhteenlaskeminen

Excelin SUMMA-funktio ei toimi, jos yrität laskea yhteen alueen, joka sisältää virhearvon, kuten #PUUTTUU. Tässä esimerkissä näytetään, miten voit laskea yhteen Tiedot-nimisen alueen, joka sisältää virheitä.

=SUMMA(JOS(ONVIRHE(Tiedot);"";Tiedot))

Kaava luo uuden taulukon, joka sisältää alkuperäiset arvot lukuun ottamatta virhearvoja. Sisimmistä funktioista aloitettaessa ONVIRHE-funktio etsii virheitä solualueelta (Tiedot). JOS-funktio palauttaa tietyn arvon, jos määrittämäsi arvo on TOSI, ja tietyn arvon, jos määrittämäsi arvo on EPÄTOSI. In this case, it returns empty strings ("") for all error values because they evaluate to TRUE, and it returns the remaining values from the range (Data) because they evaluate to FALSE, meaning that they don't contain error values. The SUM function then calculates the total for the filtered array.

Alueen virhearvojen määrän laskeminen

Tässä esimerkissä käytetään samantyyppistä kaavaa kuin edellisessä esimerkissä, mutta kaava palauttaa Tiedot-alueen virhearvojen määrän sen sijaan, että virhearvot suodatettaisiin pois:

=SUMMA(JOS(ONVIRHE(Tiedot);1;0))

Tämä kaava luo matriisin, joka sisältää arvon 1 soluille, joissa on virheitä, ja arvon 0 soluille, joissa ei ole virheitä. Voit yksinkertaistaa kaavaa ja saada saman tuloksen poistamalla JOS-funktion kolmannen argumentin:

=SUMMA(JOS(ONVIRHE(Tiedot);1))

Jos et määritä argumenttia, JOS-funktio palauttaa arvon EPÄTOSI, jos solu ei sisällä virhearvoa. Voit yksinkertaistaa kaavaa edelleen:

=SUMMA(JOS(ONVIRHE(Tiedot)*1))

Tämä kaava toimii, koska TOSI*1=1 ja EPÄTOSI*1=0.

Arvojen laskeminen yhteen ehtojen perusteella

Saatat joutua laskemaan arvot yhteen ehtojen perusteella. Esimerkiksi seuraava matriisikaava laskee yhteen vain positiiviset kokonaisluvut Myynti-nimisellä alueella:

=SUMMA(JOS(Myynti>0;Myynti))

JOS-funktio luo positiivisten arvojen ja epätosien arvojen matriisin. SUMMA-funktio ohittaa virheelliset arvot, koska 0+0=0. Kaavassa käytettävä solualue voi sisältää haluamasi määrän rivejä ja sarakkeita.

Voit myös laskea yhteen arvot, jotka vastaavat useampaa kuin yhtä ehtoa. Esimerkiksi seuraava matriisikaava laskee arvot, jotka ovat suurempia kuin 0, mutta pienempiä tai yhtä suuria kuin 5:

=SUMMA(Myynti>0)*(Myynti<=5)*(Myynti))

Huomaa, että tämä kaava palauttaa virheen, jos alue sisältää ei-numeerisia soluja.

Voit myös luoda matriisikaavoja, jotka käyttävät TAI-ehtoa. Voit esimerkiksi laskea yhteen arvot, jotka ovat pienempiä kuin 5 tai suurempia kuin 15:

=SUMMA(JOS((Myynti<5)+(Myynti>15);Myynti))

JOS-funktio etsii kaikki arvot, jotka ovat pienempiä kuin 5 tai suurempia kuin 15 ja siirtää arvot sitten SUMMA-funktiolle.

Matriisikaavoissa ei voi käyttää suoraan JA- ja TAI-funktioita, koska nämä funktiot palauttavat yksittäisen tuloksen (joko TOSI tai EPÄTOSI) ja matriisifunktiot edellyttävät tulosmatriiseja. Voit ohittaa ongelman käyttämällä edellisessä kaavassa esiteltyä logiikkaa. In other words, you perform math operations, such as addition or multiplication, on values that meet the OR or AND condition.

Nollat pois jättävän keskiarvon laskeminen

Tässä esimerkissä näytetään, miten voit poistaa nollat alueelta, kun haluat laskea alueen arvojen keskiarvon. Kaavassa käytetään Myynti-nimistä tietoaluetta:

=KESKIARVO(JOS(Myynti<>0;Myynti))

JOS-funktio luo matriisin arvoista, jotka ovat eri suuria kuin 0, ja siirtää arvot sitten KESKIARVO-funktiolle.

Kahden solualueen välisten eroavaisuuksien määrän laskeminen

This array formula compares the values in two ranges of cells named MyData and YourData and returns the number of differences between the two. If the contents of the two ranges are identical, the formula returns 0. Jotta voit käyttää tätä kaavaa, solualueiden on oltava samankokoisia ja samasta dimensiosta (jos esimerkiksi MyData on kolmen rivin ja viiden sarakkeen alue, YourDatan on oltava myös kolme riviä ja viisi saraketta):

=SUMMA(JOS(MyData=YourData,0,1))

Kaava luo uuden matriisin, joka on samankokoinen kuin vertailtavat alueet. JOS-funktio lisää matriisiin arvon 0 ja arvon 1 (0 tarkoittaa eroavaisuuksia ja 1 identtisiä soluja). SUMMA-funktio palauttaa matriisin arvojen summan.

Voit yksinkertaistaa kaavaa seuraavasti:

=SUMMA(1*(MyData<>YourData))

Tämä kaava toimii samalla tavalla kuin alueen virhearvoja laskeva kaava, koska TOSI*1=1 ja EPÄTOSI*1=0.

Alueen suurimman arvon sijainnin etsiminen

Tämä matriisikaava palauttaa yksisarakkeisen Tiedot-nimisen alueen suurimman arvon rivinumeron:

=MIN(JOS(Tiedot=MAKS(Tiedot);RIVI(Tiedot);""))

JOS-funktio luo uuden matriisin, joka vastaa Tiedot-aluetta. Jos solu sisältää alueen suurimman arvon, matriisissa on rivinumero. Muissa tapauksissa matriisi sisältää tyhjän merkkijonon (""). MIN-funktio käyttää uutta matriisia toisena argumenttinaan ja palauttaa pienimmän arvon, joka vastaa Tiedot-alueen suurimman arvon rivinumeroa. Jos Tiedot-alueella on useita täysin samanlaisia suurimpia arvoja, kaava palauttaa ensimmäisen arvon rivinumeron.

Jos haluat selvittää suurimman arvon todellisen solun osoitteen, käytä seuraavaa kaavaa:

=OSOITE(MIN(JOS(Tiedot=MAKS(Tiedot);RIVI(Tiedot);""));SARAKE(Tiedot))