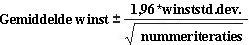Dit artikel is een bewerking van Microsoft Excel Data Analysis and Business Modeling door Wayne L. Winston.
Overzicht
- Wie gebruikt Monte Carlo-simulatie?
- Wat gebeurt er wanneer u =ASELECT() typt in een cel?
- Hoe kunt u waarden van een discrete willekeurige variabele simuleren?
- Hoe kunt u waarden van een normale willekeurige variabele simuleren?
- Hoe kan een bedrijf dat wenskaarten maakt, bepalen hoeveel kaarten moeten worden geproduceerd?
We willen graag de waarschijnlijkheid van onzekere gebeurtenissen nauwkeurig inschatten. Bijvoorbeeld: hoe groot is de kans dat de cashflows van een nieuw product een positieve netto huidige waarde (NHW) hebben? Wat is de risicofactor van onze beleggingsportefeuille? Monte Carlo-simulatie stelt ons in staat om situaties met onzekerheid te modelleren en ze vervolgens duizenden keren op een computer uit te spelen.
Opmerking
De naam Monte Carlo-simulatie komt van de computersimulaties die in de jaren 1930 en 1940 werden uitgevoerd om de waarschijnlijkheid in te schatten dat de kettingreactie die nodig was om een atoombom te laten ontploffen met succes zou werken. De natuurkundigen die bij dit werk betrokken waren, waren grote fans van gokken, dus gaven ze de simulaties de codenaam Monte Carlo.
In de volgende vijf hoofdstukken ziet u voorbeelden van hoe u Excel kunt gebruiken om Monte Carlo-simulaties uit te voeren.
Wie gebruikt Monte Carlo-simulatie?
Veel bedrijven gebruiken Monte Carlo-simulatie als een belangrijk onderdeel van hun besluitvormingsproces. Hier volgen enkele voorbeelden.
- General Motors, Proctor and Gamble, Pfizer, Bristol-Myers Squibb en Eli Lilly gebruiken simulatie om zowel het gemiddelde rendement als de risicofactor van nieuwe producten te schatten. Bij GM wordt deze informatie door de CEO gebruikt om te bepalen welke producten op de markt komen.
- GM gebruikt simulatie voor activiteiten zoals het voorspellen van netto-inkomsten voor het bedrijf, het voorspellen van structurele en inkoopkosten en het bepalen van de gevoeligheid voor verschillende soorten risico's (zoals rentewijzigingen en wisselkoersschommelingen).
- Lilly gebruikt simulatie om de optimale plantcapaciteit voor elk medicijn te bepalen.
- Proctor and Gamble gebruikt simulatie om valutarisico's te modelleren en optimaal af te dekken.
- Sears gebruikt simulatie om te bepalen hoeveel eenheden van elke productlijn bij leveranciers moeten worden besteld, bijvoorbeeld het aantal Dockers-broeken dat dit jaar moet worden besteld.
- Olie- en farmaceutische bedrijven gebruiken simulatie om 'echte opties' te waarderen, zoals de waarde van een optie om een project uit te breiden, te contracteren of uit te stellen.
- Financiële planners gebruiken Monte Carlo-simulatie om optimale beleggingsstrategieën te bepalen voor het pensioen van hun klanten.
Wat gebeurt er wanneer u =ASELECT() typt in een cel?
Wanneer u de formule =ASELECT() in een cel typt, krijgt u een getal waarvan het even waarschijnlijk is dat wordt uitgegaan van een waarde tussen 0 en 1. Dus ongeveer 25 procent van de tijd zou u een getal moeten krijgen dat kleiner is dan of gelijk is aan 0,25; Ongeveer 10 procent van de tijd moet u een getal krijgen dat minimaal 0,90 is, enzovoort. Om te laten zien hoe de functie RAND werkt, bekijkt u het bestand Randdemo.xlsx in afbeelding 60-1.
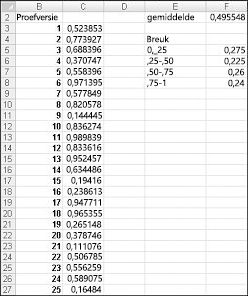
Opmerking
Wanneer u het bestand Randdemo.xlsx opent, ziet u niet dezelfde willekeurige getallen als in afbeelding 60-1. Met de functie ASELECT worden de gegenereerde getallen altijd automatisch opnieuw berekend wanneer een werkblad wordt geopend of wanneer nieuwe informatie wordt ingevoerd in het werkblad.
Kopieer eerst de formule =ASELECT()) van cel C3 naar C4:C402. Vervolgens geeft u het bereik de naam C3:C402 Gegevens. Vervolgens kunt u in kolom F het gemiddelde bijhouden van de 400 willekeurige getallen (cel F2) en de functie AANTAL.ALS gebruiken om de breuken te bepalen die tussen 0 en 0,25, 0,25 en 0,50, 0,50 en 0,75, en 0,75 en 1 liggen. Als u op F9 drukt, worden de willekeurige getallen opnieuw berekend. U ziet dat het gemiddelde van de 400 getallen altijd ongeveer 0,5 is en dat ongeveer 25 procent van de resultaten in intervallen van 0,25 valt. Deze resultaten komen overeen met de definitie van een willekeurig getal. De waarden die door ASELECT in verschillende cellen worden gegenereerd, zijn onafhankelijk. Als het willekeurige getal dat in cel C3 wordt gegenereerd bijvoorbeeld een groot getal is (bijvoorbeeld 0,99), zegt dit niets over de waarden van de andere willekeurige getallen die worden gegenereerd.
Hoe kunt u waarden van een discrete willekeurige variabele simuleren?
Stel dat de vraag naar een kalender wordt bepaald door de volgende discrete willekeurige variabele:
| Vraag | kans |
|---|---|
| 10.000 | 0,10 |
| 20.000 | 0,35 |
| 40,000 | 0,3 |
| 60.000 | 0,25 |
Hoe kunnen we deze vraag naar kalenders vele malen laten afspelen of simuleren in Excel? De truc is om elke mogelijke waarde van de functie ASELECT te koppelen aan een mogelijke vraag naar kalenders. De volgende toewijzing zorgt ervoor dat een vraag van 10.000 10 procent van de tijd voorkomt, enzovoort.
| Vraag | Willekeurig toegewezen getal |
|---|---|
| 10.000 | Kleiner dan 0,10 |
| 20.000 | Groter dan of gelijk aan 0,10 en kleiner dan 0,45 |
| 40,000 | Groter dan of gelijk aan 0,45 en kleiner dan 0,75 |
| 60.000 | Groter dan of gelijk aan 0,75 |
Om de simulatie van de vraag te demonstreren, kijkt u naar het bestand Discretesim.xlsx, weergegeven in figuur 60-2 op de volgende pagina.
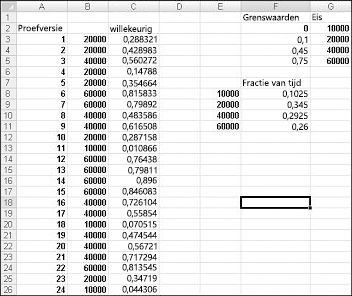
De sleutel tot onze simulatie is om een willekeurig getal te gebruiken om een zoekopdracht uit het tabelbereik F2:G5 (named lookup) te starten. Willekeurige getallen groter dan of gelijk aan 0 en kleiner dan 0,10 leveren een vraag van 10.000 op; willekeurige getallen groter dan of gelijk aan 0,10 en kleiner dan 0,45 leveren een eis van 20.000 op; willekeurige getallen groter dan of gelijk aan 0,45 en kleiner dan 0,75 leveren een eis van 40.000 op; en willekeurige getallen groter dan of gelijk aan 0,75 leveren een vraag van 60.000 op. U genereert 400 willekeurige getallen door de formule ASELECT()) te kopiëren van C3 naar C4:C402. Vervolgens genereert u 400 experimenten, of iteraties, van de kalendervraag door de formule VERT.ZOEKEN(C3;zoeken;2) te kopiëren van B3 naar B4:B402. Deze formule zorgt ervoor dat elk willekeurig getal kleiner dan 0,10 een vraag van 10.000 genereert, elk willekeurig getal tussen 0,10 en 0,45 een vraag van 20.000, enzovoort. Gebruik de functie AANTAL.ALS in het celbereik F8:F11 om te bepalen welk deel van de 400 iteraties elke vraag oplevert. Wanneer we op F9 drukken om de willekeurige getallen opnieuw te berekenen, liggen de gesimuleerde kansen dicht bij onze veronderstelde vraagkansen.
Hoe kunt u waarden van een normale willekeurige variabele simuleren?
Als u in een willekeurige cel de formule NORM.INV(rand(),mu,sigma) typt, genereert u een gesimuleerde waarde van een normale willekeurige variabele met een gemiddelde mu en standaarddeviatie sigma. Deze procedure wordt geïllustreerd in het bestand Normalsim.xlsx, weergegeven in figuur 60-3.
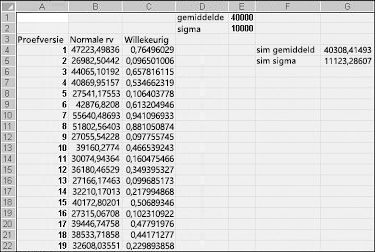
Laten we aannemen dat we 400 experimenten, of iteraties, willen simuleren voor een normale willekeurige variabele met een gemiddelde van 40.000 en een standaarddeviatie van 10.000. (U kunt deze waarden typen in de cellen E1 en E2 en de cellen respectievelijk gemiddelde en sigma noemen.) Als u de formule =ASELECT() kopieert van C4 naar C5:C403, worden 400 verschillende willekeurige getallen gegenereerd. Wanneer u de formule B4 naar B5:B403 kopieert, genereert NORM.INV(C4,gemiddelde,sigma) 400 verschillende experimentwaarden uit een normale willekeurige variabele met een gemiddelde van 40.000 en een standaarddeviatie van 10.000. Wanneer we op F9 drukken om de willekeurige getallen opnieuw te berekenen, blijft het gemiddelde dicht bij 40.000 en de standaarddeviatie dicht bij 10.000.
Voor een willekeurig getal x genereert de formule NORM.INV(p,mu,sigma) het pde percentiel van een normale willekeurige variabele met een gemiddelde mu en een standaarddeviatie sigma. Het willekeurige getal 0,77 in cel C4 (zie Figuur 60-3) genereert bijvoorbeeld in cel B4 ongeveer het 77e percentiel van een normale willekeurige variabele met een gemiddelde van 40.000 en een standaarddeviatie van 10.000.
Hoe kan een bedrijf dat wenskaarten maakt, bepalen hoeveel kaarten moeten worden geproduceerd?
In dit gedeelte ziet u hoe Monte Carlo-simulatie kan worden gebruikt als besluitvormingstool. Stel dat de vraag naar een Valentijnsdagkaart wordt bepaald door de volgende discrete willekeurige variabele:
| Vraag | kans |
|---|---|
| 10.000 | 0,10 |
| 20.000 | 0,35 |
| 40,000 | 0,3 |
| 60.000 | 0,25 |
De wenskaart wordt verkocht voor $ 4,00 en de variabele productiekosten van elke kaart bedragen $ 1,50. Overgebleven kaarten moeten worden weggegooid voor $ 0.20 per kaart. Hoeveel kaarten moeten er worden afgedrukt?
In principe simuleren we elke mogelijke productiehoeveelheid (10.000, 20.000, 40.000 of 60.000) vele malen (bijvoorbeeld 1000 iteraties). Vervolgens bepalen we welke orderhoeveelheid de maximale gemiddelde winst oplevert over de 1000 iteraties. U vindt de gegevens voor deze sectie in het bestand Valentine.xlsx, weergegeven in afbeelding 60-4. U wijst de bereiknamen in de cellen B1:B11 toe aan cellen C1:C11. Het celbereik G3:H6 wordt toegewezen aan het opzoeken van namen. De parameters voor verkoopprijs en kostprijs worden ingevoerd in cellen C4:C6.
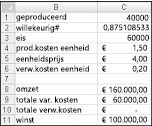
U kunt een proefproductiehoeveelheid (40.000 in dit voorbeeld) invoeren in cel C1. Maak vervolgens een willekeurig getal in cel C2 met de formule =ASELECT(). Zoals eerder is beschreven, simuleert u de vraag naar de kaart in cel C3 met de formule VERT.ZOEKEN(rand,zoeken,2). (In de formule VERT.ZOEKEN is rand de celnaam die is toegewezen aan cel C3, niet de functie RAND.)
Het aantal verkochte eenheden is het kleinste van onze productiehoeveelheid en vraag. In cel C8 berekent u onze opbrengst met de formule MIN(geproduceerd;vraag)*unit_price. In cel C9 berekent u de totale productiekosten met de geproduceerde formule*unit_prod_cost.
Als we meer kaarten produceren dan er vraag naar is, is het aantal overgebleven eenheden gelijk aan de productie minus de vraag; Anders blijven er geen eenheden over. We berekenen de verwijderingskosten in cel C10 met de formule unit_disp_cost*ALS(geproduceerde>vraag;geproduceerd–vraag;0). In cel C11 ten slotte berekenen we onze winst als opbrengst – total_var_cost-total_disposing_cost.
We willen graag een efficiënte manier om vaak op F9 te drukken (bijvoorbeeld 1000) voor elke productiehoeveelheid en onze verwachte winst voor elke hoeveelheid te tellen. Dit is er een waarin een tweerichtingsgegevenstabel ons te hulp schiet. (Zie hoofdstuk 15, 'Gevoeligheidsanalyse met gegevenstabellen' voor meer informatie over gegevenstabellen.) De gegevenstabel die in dit voorbeeld wordt gebruikt, wordt weergegeven in afbeelding 60-5.
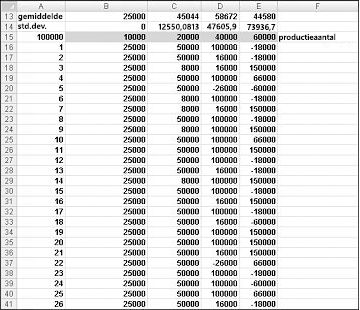
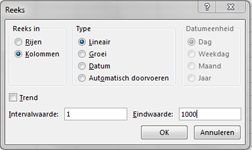
Voer in het celbereik A16:A1015 de getallen 1-1000 in (overeenkomend met onze 1000 experimenten). Een makkelijke manier om deze waarden te maken is eerst 1 in cel A16 in te voeren. Selecteer de cel en klik vervolgens op het tabblad Start in de groep Bewerken op Opvullen en selecteer Reeks om het dialoogvenster Reeks weer te geven. Voer in het dialoogvenster Reeks , weergegeven in afbeelding 60-6, een intervalwaarde van 1 en een stopwaarde van 1000 in. Selecteer in het gebied Reeksen in de optie Kolommen en klik vervolgens op OK. De getallen 1-1000 worden ingevoerd in kolom A vanaf cel A16.
Vervolgens voeren we de mogelijke productiegrootheden (10.000, 20.000, 40.000, 60.000) in de cellen B15:E15 in. We willen de winst berekenen voor elk proefnummer (1 tot en met 1000) en elke productiehoeveelheid. We verwijzen naar de formule voor winst (berekend in cel C11) in de cel linksboven in onze gegevenstabel (A15) door =C11 in te voeren.
We zijn nu klaar om Excel te misleiden om 1000 iteraties van de vraag voor elke productiehoeveelheid te simuleren. Selecteer het tabelbereik (A15:E1014) en klik in de groep Hulpmiddelen voor gegevens op het tabblad Gegevens op Wat-als-analyse en selecteer Gegevenstabel. Als u een tweerichtingsgegevenstabel wilt instellen, kiest u onze productiehoeveelheid (cel C1) als rij-invoercel en selecteert u een lege cel (we selecteren cel I14) als kolominvoercel. Nadat u op OK hebt geklikt, worden in Excel 1000 vraagwaarden voor elke bestelhoeveelheid gesimuleerd.
Als u wilt weten waarom dit werkt, kunt u kijken naar de waarden die door de gegevenstabel in het celbereik C16:C1015 worden geplaatst. Voor elk van deze cellen wordt in cel C1 de waarde 20.000 gebruikt. In C16 wordt de kolominvoercelwaarde 1 in een lege cel geplaatst en wordt het willekeurige getal in cel C2 opnieuw berekend. De bijbehorende winst wordt vervolgens in cel C16 opgenomen. Vervolgens wordt de kolomcelinvoerwaarde van 2 in een lege cel geplaatst en wordt het willekeurige getal in C2 opnieuw berekend. De bijbehorende winst wordt ingevoerd in cel C17.
Door de formule GEMIDDELDE(B16:B1015) te kopiëren van cel B13 naar C13:E13, berekenen we de gemiddelde gesimuleerde winst voor elke productiehoeveelheid. Door de formule STDEV(B16:B1015) te kopiëren van cel B14 naar C14:E14, berekenen we de standaarddeviatie van onze gesimuleerde winst voor elke bestelhoeveelheid. Elke keer dat we op F9 drukken, worden 1000 iteraties van de vraag gesimuleerd voor elke orderhoeveelheid. Het produceren van 40.000 kaarten levert altijd de grootste verwachte winst op. Daarom lijkt het erop dat het produceren van 40.000 kaarten de juiste beslissing is.
De impact van risico's op onze beslissing Als we 20.000 in plaats van 40.000 kaarten zouden produceren, daalt onze verwachte winst met ongeveer 22%, maar daalt ons risico (gemeten aan de hand van de standaarddeviatie van de winst) met bijna 73%. Daarom, als we extreem afkerig zijn van risico's, kan het produceren van 20.000 kaarten de juiste beslissing zijn. Overigens heeft het produceren van 10.000 kaarten altijd een standaarddeviatie van 0 kaarten, want als we 10.000 kaarten produceren, verkopen we ze altijd allemaal zonder restjes.
Opmerking
In deze werkmap is de optie Berekening ingesteld op Automatisch behalve tabellen. (Gebruik de opdracht Berekening in de groep Berekening op het tabblad Formules.) Deze instelling zorgt ervoor dat de gegevenstabel alleen opnieuw wordt berekend als we op F9 drukken. Dit is een goed idee omdat een grote gegevenstabel uw werk zal vertragen als het elke keer dat u iets in het werkblad typt, opnieuw wordt berekend. Houd er rekening mee dat in dit voorbeeld de gemiddelde winst verandert wanneer u op F9 drukt. Dit komt omdat telkens wanneer u op F9 drukt, een andere reeks van 1000 willekeurige getallen wordt gebruikt om eisen voor elke bestelhoeveelheid te genereren.
Betrouwbaarheidsinterval voor gemiddelde winst Een natuurlijke vraag om in deze situatie te stellen is: in welk interval zijn we er 95 procent zeker van dat de werkelijke gemiddelde winst zal dalen? Dit interval wordt het 95 procent betrouwbaarheidsinterval voor de gemiddelde winst genoemd. Een betrouwbaarheidsinterval van 95 procent voor het gemiddelde van een simulatie-uitvoer wordt berekend met de volgende formule:
In cel J11 berekent u de ondergrens voor het betrouwbaarheidsinterval van 95 procent van de gemiddelde winst als er 40.000 kalenders zijn geproduceerd met de formule D13–1,96*D14/WORTEL(1000). In cel J12 berekent u de bovengrens van het 95 procent-betrouwbaarheidsinterval met de formule D13+1,96*D14/SQRT(1000). Deze berekeningen zijn weergegeven in figuur 60-7.
We zijn er 95 procent zeker van dat onze gemiddelde winst bij 40.000 bestelde kalenders tussen de $ 56.687 en $ 62.589 ligt.
Problemen
Een GMC-dealer is van mening dat de vraag naar gezanten voor 2005 normaal zal worden verdeeld met een gemiddelde van 200 en een standaarddeviatie van 30. Zijn kosten voor het ontvangen van een gezant bedragen $ 25.000 en hij verkoopt een gezant voor $ 40.000. De helft van alle gezanten die niet voor de volle prijs worden verkocht, kan worden verkocht voor $ 30.000. Hij overweegt 200, 220, 240, 260, 280 of 300 gezanten te bestellen. Hoeveel moet hij er bestellen?
Een kleine supermarkt probeert te bepalen hoeveel exemplaren van het tijdschrift People ze elke week moeten bestellen. Ze denken dat hun vraag naar People wordt bepaald door de volgende discrete willekeurige variabele:
Vraag kans 15 0,10 20 0.20 25 0.30 30 0,25 35 0,15 De supermarkt betaalt $ 1,00 voor elk exemplaar van People en verkoopt het voor $ 1,95. Elk onverkocht exemplaar kan worden geretourneerd voor $ 0,50. Hoeveel exemplaren van People moet de winkel bestellen?
Meer hulp nodig?
U kunt altijd uw vraag stellen aan een expert in de Excel Tech Community of ondersteuning vragen in Community's.