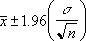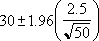Retorna o intervalo de confiança para uma média populacional com uma distribuição normal. O intervalo de confiança é um intervalo em ambos os lados de uma média de exemplo. Por exemplo, se você pedir um produto por email, poderá determinar, com um determinado nível de confiança, o mais antigo e mais recente que o produto chegará.
Sintaxe
CONFIDENCE(alpha,standard_dev,size)
Alfa é o nível de significância usado para calcular o nível de confiança. O nível de confiança é igual a 100*(1 - alfa)% ou, em outras palavras, um alfa de 0,05 indica um nível de confiança de 95%.
Desv_padrão é o desvio padrão da população para o intervalo de dados e supõe-se que seja conhecido.
Tamanho é o tamanho do exemplo.
Comentários
-
Se algum argumento for não numérico, o CONFIDENCE retornará o #VALUE! valor de erro.
-
Se alfa ≤ 0 ou alfa ≥ 1, o CONFIDENCE retornará o #NUM! valor de erro.
-
Se standard_dev ≤ 0, CONFIDENCE retornará o #NUM! valor de erro.
-
Se tamanho não for um inteiro, será truncado.
-
Se o tamanho < 1, o CONFIDENCE retornará o #NUM! valor de erro.
-
Se considerarmos que alfa é igual a 0,05, precisaremos calcular a área sob a curva normal padrão que é igual a (1 - alfa) ou 95%. Este valor é ± 1,96. O intervalo de confiança é, portanto:
Exemplo
Suponha que observemos que, em nossa amostra de 50 viajantes, o comprimento médio da viagem para o trabalho é de 30 minutos com um desvio padrão populacional de 2,5. Podemos estar 95% confiantes de que a média da população está no intervalo:
|
Alfa |
StdDev |
Tamanho |
Fórmula |
Descrição (Resultado) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=CONFIDENCE([Alpha],[StdDev],[Size]) |
O intervalo de confiança para uma média da população. Em outras palavras, o comprimento médio da viagem para o trabalho é igual a 30 ± 0,692951 minutos, ou 29,3 a 30,7 minutos. (0.692951) |