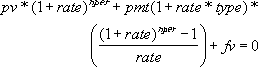Retorna o valor atual de um investimento. O valor presente é o valor total correspondente ao valor atual de uma série de pagamentos futuros. Por exemplo, quando você empresta dinheiro, o valor do empréstimo é o valor presente para o credor.
Sintaxe
PV(rate,nper,pmt,fv,type)
Taxa é a taxa de juros por período. Por exemplo, se você tiver um empréstimo para um automóvel com taxa de de juros de 10% ano ano e fizer pagamentos mensais, sua taxa de juros mensal será de 10%/12 ou 0,83%. Você deveria inserir 10%/12 ou 0,83%, ou 0,0083, na fórmula como taxa.
Nper é o número total de períodos de pagamento em uma anuidade. Por exemplo, se você conseguir um empréstimo de carro de quatro anos e fizer pagamentos mensais, seu empréstimo terá 4*12 (ou 48) períodos. Você deveria inserir 48 na fórmula para nper.
Pgto é o pagamento feito a cada período e não pode ser alterado ao longo da vida da anuidade. Geralmente, pgto inclui o principal e os juros e nenhuma outra taxa ou tributo. Por exemplo, os pagamentos mensais de R$ 10.000 de um empréstimo de quatro anos para um carro serão de R$ 263,33. Você deveria inserir -263,33 na fórmula como pgto. Se pgto for omitido, você deverá incluir o argumento vf.
Vf é o valor futuro ou um saldo em caixa que você deseja alcançar após o último pagamento ser feito. Se vf for omitido, será considerado 0 (o valor futuro de um empréstimo, por exemplo, é 0). Por exemplo, se você deseja economizar R$ 50.000 para pagar um projeto especial em 18 anos, então o valor futuro será de R$ 50.000. Você poderia então fazer uma estimativa conservadora na taxa de juros e concluir quanto economizaria por mês. Se vf for omitido, você deverá incluir o argumento pgto.
Tipo é o número 0 ou 1 e indica quando os pagamentos são devidos.
|
Definir tipo como |
Se os vencimentos forem |
|---|---|
|
0 ou omitido |
No final do período |
|
1 |
No início do período |
Comentários
-
Certifique-se de que esteja sendo consistente quanto às unidades usadas para especificar taxa e nper. Se fizer pagamentos mensais de um empréstimo de quatro anos com taxa de juros de 12% ao ano, use 12%/12 para taxa e 4*12 para nper. Se você fizer pagamentos anuais para o mesmo empréstimo, use 12% para taxa e 4 para nper.
-
As seguintes funções se aplicam a anuidades: FV; IPGTO; PGTO; PPGTO; PV; e RATE. Uma anuidade é uma série de constantes pagamentos em caixa realizados por um período contínuo. Por exemplo, um empréstimo para um carro ou um prestação é uma anuidade. Para obter mais informações, consulte a descrição para cada função de anuidade.
-
Nas funções de anuidade, o saldo em dinheiro pago, como depósitos em poupanças, é representado por um número negativo; o saldo em dinheiro recebido, como cheques de dividendos é representado por números positivos. Por exemplo, um depósito de R$ 1.000 no banco deveria ser representado pelo argumento -1000 se você for o depositante e pelo argumento 1000 se você for o banco.
-
Um argumento financeiro é resolvido em termos dos outros. Se a taxa não for 0, então:
Se a taxa for 0, então:
(pgto * nper) + vp + vf = 0
Exemplo
No exemplo a seguir:
-
Pmt é o dinheiro pago de uma anuidade de seguro no final de cada mês.
-
Taxa é a taxa de juros obtida sobre o dinheiro pago.
-
Nper é o ano em que o dinheiro será pago.
A taxa de juros é dividida por 12 para obter uma taxa mensal. Os anos em que o dinheiro é pago é multiplicado por 12 para obter o número de pagamentos.
|
Pgto |
Taxa |
Nper |
Fórmula |
Descrição (Resultado) |
|---|---|---|---|---|
|
500 |
8% |
20 |
=PV([Rate]/12, 12*[Nper], [Pmt], , 0) |
Valor presente de uma anuidade com os argumentos especificados (-59.777,15). |
O resultado é negativo porque representa o dinheiro que você pagaria, um fluxo de caixa de saída. Se você for solicitado a pagar (60.000) pela anuidade, você determinará que este não seria um bom investimento porque o valor presente da anuidade (59.777,15) é menor do que o que você é solicitado a pagar.