Importante: O suporte para Office 2016 e Office 2019 terminou em 14 de outubro de 2025. Atualize para o Microsoft 365 para trabalhar em qualquer lugar em qualquer dispositivo e continuar a receber suporte. Obter o Microsoft 365
Este artigo discute o uso do Solver, um programa de suplemento do Microsoft Excel que você pode usar para análise de e se, para determinar um mix de produtos ideal.
Como posso determinar o mix mensal de produtos que maximiza a rentabilidade?
As empresas geralmente precisam determinar a quantidade de cada produto a ser produzido mensalmente. Em sua forma mais simples, o problema do mix de produtos envolve como determinar a quantidade de cada produto que deve ser produzido durante um mês para maximizar os lucros. O mix de produtos geralmente deve seguir as seguintes restrições:
-
O mix de produtos não pode usar mais recursos do que estão disponíveis.
-
Há uma demanda limitada por cada produto. Não podemos produzir mais de um produto durante um mês do que a demanda determina, porque o excesso de produção é desperdiçado (por exemplo, uma droga perecível).
Agora vamos resolver o exemplo a seguir do problema do mix de produtos. Você pode encontrar a solução para esse problema no Prodmix.xlsx de arquivo, mostrado na Figura 27-1.
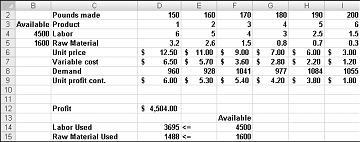
Digamos que trabalhamos para uma empresa farmacêutica que produz seis produtos diferentes em sua fábrica. A produção de cada produto requer trabalho e matéria-prima. A linha 4 na Figura 27-1 mostra as horas de trabalho de trabalho necessárias para produzir um quilo de cada produto, e a linha 5 mostra os quilos da matéria-prima necessária para produzir um quilo de cada produto. Por exemplo, produzir um quilo de Produto 1 requer seis horas de trabalho de parto e 3,2 quilos de matéria-prima. Para cada droga, o preço por libra é dado na linha 6, o custo unitário por libra é dado na linha 7, e a contribuição de lucro por libra é dada na linha 9. Por exemplo, o Produto 2 é vendido por US$ 11,00 por libra, incorre em um custo unitário de US$ 5,70 por libra e contribui com um lucro de US$ 5,30 por libra. A demanda do mês por cada droga é dada na linha 8. Por exemplo, a demanda pelo Produto 3 é de 1041 libras. Este mês, 4.500 horas de trabalho de parto e 1600 quilos de matéria-prima estão disponíveis. Como essa empresa pode maximizar seu lucro mensal?
Se não soubéssemos nada sobre o Excel Solver, atacaríamos esse problema construindo uma planilha para controlar o lucro e o uso de recursos associados ao mix de produtos. Em seguida, usaríamos a avaliação e o erro para variar o mix de produtos para otimizar o lucro sem usar mais mão-de-obra ou matéria-prima do que está disponível e sem produzir nenhuma droga acima da demanda. Usamos o Solver nesse processo somente na fase de avaliação e erro. Essencialmente, o Solver é um mecanismo de otimização que executa perfeitamente a pesquisa de tentativa e erro.
Uma chave para resolver o problema do mix de produtos é calcular com eficiência o uso de recursos e o lucro associados a qualquer determinado mix de produtos. Uma ferramenta importante que podemos usar para fazer essa computação é a função SOMARPRODUTO. A função SOMARPRODUTO multiplica valores correspondentes em intervalos de células e retorna a soma desses valores. Cada intervalo de células usado em uma avaliação SOMARPRODUTO deve ter as mesmas dimensões, o que implica que você pode usar SOMARPRODUTO com duas linhas ou duas colunas, mas não com uma coluna e uma linha.
Como exemplo de como podemos usar a função SOMARPRODUTO em nosso exemplo de mix de produtos, vamos tentar calcular nosso uso de recursos. Nosso uso de mão-de-obra é calculado por
(Trabalho usado por quilo de droga 1)*(Droga 1 libras produzida)+ (Trabalho usado por quilo de droga 2)*(Droga 2 libras produzida) + ... (Trabalho usado por quilo de droga 6)*(Droga 6 libras produzida)
Poderíamos calcular o uso do trabalho de forma mais tediosa como D2*D4+E2*E4+F2*F4+G2*G2*G4+H2*H4+I2*I4. Da mesma forma, o uso de matéria-prima poderia ser calculado como D2*D5+E2*E5+F2*F5+G2*G2*G5+H2*H5+I2*I5. No entanto, inserir essas fórmulas em uma planilha para seis produtos é demorado. Imagine quanto tempo levaria se você trabalhasse com uma empresa que produziu, por exemplo, 50 produtos em sua fábrica. Uma maneira muito mais fácil de calcular o uso de trabalho e matéria-prima é copiar de D14 para D15 a fórmula SOMARPRODUTO($D$2:$I$2,D4:I4). Essa fórmula calcula D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I2*I4 (que é nosso uso de trabalho), mas é muito mais fácil de inserir! Observe que uso o sinal $com o intervalo D2:I2 para que, quando copiar a fórmula, ainda capture o mix de produtos da linha 2. A fórmula na célula D15 calcula o uso de matéria-prima.
De maneira semelhante, nosso lucro é determinado por
(Lucro da droga 1 por libra)*(Droga 1 libras produzida) + (Lucro da droga 2 por libra)*(Droga 2 libras produzida) + ... (Lucro da droga 6 por libra)*(Droga 6 libras produzida)
O lucro é facilmente calculado na célula D12 com a fórmula SOMARPRODUTO(D9:I9,$D$2:$I$2).
Agora podemos identificar os três componentes do nosso modelo de solver de mix de produtos.
-
Célula de destino. Nosso objetivo é maximizar o lucro (computado na célula D12).
-
Alterando células. O número de libras produzidas de cada produto (listado no intervalo de células D2:I2)
-
Restrições. Temos as seguintes restrições:
-
Não use mais trabalho ou matéria-prima do que está disponível. Ou seja, os valores nas células D14:D15 (os recursos usados) devem ser menores ou iguais aos valores nas células F14:F15 (os recursos disponíveis).
-
Não produz mais de uma droga do que está em demanda. Ou seja, os valores nas células D2:I2 (quilos produzidos de cada droga) devem ser menores ou iguais à demanda por cada droga (listada nas células D8:I8).
-
Não podemos produzir uma quantidade negativa de qualquer droga.
-
Mostrarei como inserir a célula de destino, alterando células e restrições no Solver. Em seguida, tudo o que você precisa fazer é clicar no botão Resolver para encontrar um mix de produtos com maximização de lucro!
Para começar, clique na guia Dados e, no grupo Análise, clique em Solucionar.
Observação: Conforme explicado no Capítulo 26, "Uma Introdução à Otimização com o Excel Solver", o Solver é instalado clicando no Botão do Microsoft Office e em Opções do Excel, seguido por Suplementos. Na lista Gerenciar, clique em Suplementos do Excel, marcar a caixa Suplemento do Solver e clique em OK.
A caixa de diálogo Parâmetros do Solucionador será exibida, conforme mostrado na Figura 27-2.
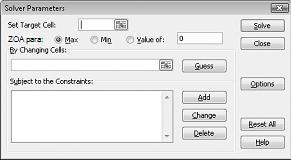
Clique na caixa Definir Célula de Destino e selecione nossa célula de lucro (célula D12). Clique na caixa Por Alterar Células e, em seguida, aponte para o intervalo D2:I2, que contém os quilos produzidos de cada droga. A caixa de diálogo agora deve parecer Figura 27-3.
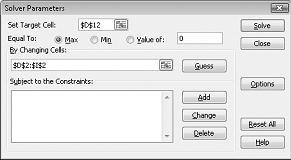
Agora estamos prontos para adicionar restrições ao modelo. Clique no botão Adicionar. Você verá a caixa de diálogo Adicionar Restrição, mostrada na Figura 27-4.
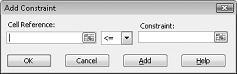
Para adicionar as restrições de uso do recurso, clique na caixa Referência de Célula e selecione o intervalo D14:D15. Selecione <= na lista do meio. Clique na caixa Restrição e selecione o intervalo de células F14:F15. A caixa de diálogo Adicionar Restrição agora deve se parecer com a Figura 27-5.
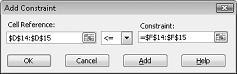
Agora garantimos que, quando o Solver tentar valores diferentes para as células em alteração, serão consideradas apenas combinações que atendam a D14<=F14 (o trabalho usado é menor ou igual ao trabalho disponível) e D15<=F15 (a matéria-prima usada é menor ou igual à matéria-prima disponível) será considerada. Clique em Adicionar para inserir as restrições de demanda. Preencha a caixa de diálogo Adicionar Restrição, conforme mostrado na Figura 27-6.
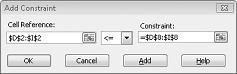
A adição dessas restrições garante que, quando o Solver tentar combinações diferentes para os valores de célula em alteração, somente combinações que satisfaçam os seguintes parâmetros serão consideradas:
-
D2<=D8 (a quantidade produzida da Droga 1 é menor ou igual à demanda por Droga 1)
-
E2<=E8 (a quantidade produzida da Droga 2 é menor ou igual à demanda por Droga 2)
-
F2<=F8 (a quantidade produzida da Droga 3 feita é menor ou igual à demanda por Droga 3)
-
G2<=G8 (a quantidade produzida da Droga 4 feita é menor ou igual à demanda por Droga 4)
-
H2<=H8 (a quantidade produzida da Droga 5 feita é menor ou igual à demanda por Droga 5)
-
I2<=I8 (a quantidade produzida da Droga 6 feita é menor ou igual à demanda por Droga 6)
Clique em OK na caixa de diálogo Adicionar Restrição. A janela Solver deve se parecer com a Figura 27-7.

Inserimos a restrição de que a alteração de células deve não ser negativa na caixa de diálogo Opções do Solucionador. Clique no botão Opções na caixa de diálogo Parâmetros do Solucionador. Verifique a caixa Assumir Modelo Linear e a caixa Assumir Não Negativo, conforme mostrado na Figura 27-8 na próxima página. Clique em OK.
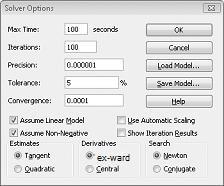
Verificar a caixa Assumir Não Negativo garante que o Solver considere apenas combinações de células de alteração nas quais cada célula em alteração pressupõe um valor não negativo. Verificamos a caixa Assumir Modelo Linear porque o problema do mix de produtos é um tipo especial de problema do Solver chamado de modelo linear. Essencialmente, um modelo solver é linear nas seguintes condições:
-
A célula de destino é calculada adicionando os termos do formulário (alterando célula)*(constante).
-
Cada restrição atende ao "requisito de modelo linear". Isso significa que cada restrição é avaliada adicionando os termos do formulário (alterando célula)*(constante) e comparando as somas com uma constante.
Por que esse problema do Solucionador é linear? Nossa célula de destino (lucro) é calculada como
(Lucro da droga 1 por libra)*(Droga 1 libras produzida) + (Lucro da droga 2 por libra)*(Droga 2 libras produzida) + ... (Lucro da droga 6 por libra)*(Droga 6 libras produzida)
Essa computação segue um padrão no qual o valor da célula de destino é derivado adicionando termos do formulário (alterando célula)*(constante).
Nossa restrição de trabalho é avaliada comparando o valor derivado de (trabalho usado por quilo de Droga 1)*(Droga 1 quilos produzido) + (Trabalho usado por quilo de Droga 2)*(Droga 2 quilos produzido)+ ... (Trabalho conoscoed por quilo de Droga 6)*(Droga 6 libras produzida) para o trabalho disponível.
Portanto, a restrição de trabalho é avaliada adicionando os termos do formulário (alterando célula)*(constante) e comparando as somas a uma constante. Tanto a restrição de mão-de-obra quanto a restrição de matéria-prima atendem ao requisito de modelo linear.
Nossas restrições de demanda tomam o formulário
(Droga 1 produzida)<=(Droga 1 Demanda) (Droga 2 produzida)<=(Droga 2 Demanda) §(Droga 6 produzida)<=(Droga 6 Demanda)
Cada restrição de demanda também atende ao requisito de modelo linear, pois cada uma é avaliada adicionando os termos do formulário (alterando célula)*(constante) e comparando as somas a uma constante.
Tendo mostrado que nosso modelo de mix de produtos é um modelo linear, por que devemos nos importar?
-
Se um modelo solver for linear e selecionarMos Assumir Modelo Linear, o Solver será garantido para encontrar a solução ideal para o modelo Solver. Se um modelo solver não for linear, o Solver poderá ou não encontrar a solução ideal.
-
Se um modelo solver for linear e selecionarMos Assumir Modelo Linear, o Solver usará um algoritmo muito eficiente (o método simplex) para encontrar a solução ideal do modelo. Se um modelo solver for linear e não selecionarMos Assumir Modelo Linear, o Solver usará um algoritmo muito ineficiente (o método GRG2) e poderá ter dificuldade em encontrar a solução ideal do modelo.
Depois de clicar em OK na caixa de diálogo Opções do Solucionador, retornamos à caixa de diálogo main Solver, mostrada anteriormente na Figura 27-7. Quando clicamos em Resolver, o Solver calcula uma solução ideal (se existir) para nosso modelo de mix de produtos. Como afirmou no Capítulo 26, uma solução ideal para o modelo de mixagem de produtos seria um conjunto de valores de células (libras produzidas de cada droga) que maximiza o lucro sobre o conjunto de todas as soluções viáveis. Novamente, uma solução viável é um conjunto de alteração de valores de célula que satisfazem todas as restrições. Os valores de célula de alteração mostrados na Figura 27-9 são uma solução viável porque todos os níveis de produção não são negativos, os níveis de produção não excedem a demanda e o uso de recursos não excede os recursos disponíveis.
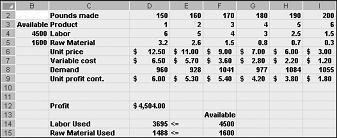
Os valores de célula de alteração mostrados na Figura 27-10 na próxima página representam uma solução inviável pelos seguintes motivos:
-
Produzimos mais da Droga 5 do que a demanda por ela.
-
Usamos mais trabalho do que o que está disponível.
-
Usamos mais matéria-prima do que o que está disponível.
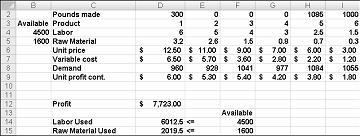
Depois de clicar em Resolver, o Solver encontra rapidamente a solução ideal mostrada na Figura 27-11. Você precisa selecionar Manter solução solver para preservar os valores ideais da solução na planilha.
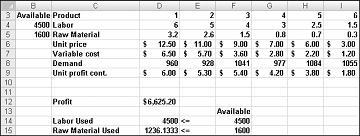
Nossa companhia farmacêutica pode maximizar seu lucro mensal a um nível de $6.625,20 produzindo 596,67 libras de Droga 4, 1084 libras de Droga 5, e nenhuma das outras drogas! Não podemos determinar se podemos obter o lucro máximo de US$ 6.625,20 de outras maneiras. Tudo o que podemos ter certeza é que, com nossos recursos limitados e demanda, não há como fazer mais de US $ 6.627,20 este mês.
Suponha que a demanda por cada produto deve ser atendida. (Consulte a planilha Sem solução viável no arquivo Prodmix.xlsx.) Em seguida, temos que alterar nossas restrições de demanda de D2:I2<=D8:I8 para D2:I2>=D8:I8. Para fazer isso, abra Solver, selecione a restrição D2:I2<=D8:I8 e clique em Alterar. A caixa de diálogo Restrição de Alteração, mostrada na Figura 27-12, é exibida.
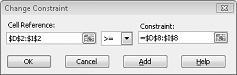
Selecione >=e clique em OK. Agora garantimos que o Solver considerará alterar apenas os valores de célula que atendem a todas as demandas. Ao clicar em Resolver, você verá a mensagem "O solucionador não conseguiu encontrar uma solução viável". Esta mensagem não significa que cometemos um erro em nosso modelo, mas sim que, com nossos recursos limitados, não podemos atender à demanda por todos os produtos. O Solver está simplesmente nos dizendo que, se quisermos atender à demanda por cada produto, precisamos adicionar mais mão-de-obra, mais matérias-primas ou mais de ambos.
Vamos ver o que acontece se permitirmos a demanda ilimitada por cada produto e permitirmos que quantidades negativas sejam produzidas de cada droga. (Você pode ver esse problema do Solucionador na planilha Definir Valores Não Convergir no arquivo Prodmix.xlsx.) Para encontrar a solução ideal para essa situação, abra Solver, clique no botão Opções e desmarque a caixa Assumir Não Negativo. Na caixa de diálogo Parâmetros do Solucionador, selecione a restrição de demanda D2:I2<=D8:I8 e clique em Excluir para remover a restrição. Quando você clica em Resolver, o Solver retorna a mensagem "Definir valores de célula não convergem". Essa mensagem significa que, se a célula de destino deve ser maximizada (como em nosso exemplo), há soluções viáveis com valores de célula de destino arbitrariamente grandes. (Se a célula de destino deve ser minimizada, a mensagem "Definir valores de célula não convergem" significa que há soluções viáveis com valores de célula de destino arbitrariamente pequenos.) Em nossa situação, ao permitir a produção negativa de uma droga, na verdade "criamos" recursos que podem ser usados para produzir quantidades arbitrariamente grandes de outras drogas. Dada a nossa demanda ilimitada, isso nos permite obter lucros ilimitados. Em uma situação real, não podemos fazer uma quantidade infinita de dinheiro. Em suma, se você vir "Definir valores não convergir", seu modelo terá um erro.
-
Suponha que nossa empresa farmacêutica possa comprar até 500 horas de trabalho a $1 a mais por hora do que os custos atuais de mão-de-obra. Como podemos maximizar o lucro?
-
Em uma fábrica de chips, quatro técnicos (A, B, C e D) produzem três produtos (Produtos 1, 2 e 3). Este mês, o fabricante de chips pode vender 80 unidades do Produto 1, 50 unidades do Produto 2 e no máximo 50 unidades do Produto 3. O Técnico A só pode fazer Produtos 1 e 3. O técnico B só pode criar Produtos 1 e 2. O técnico C só pode fazer o Produto 3. O Técnico D só pode fazer o Produto 2. Para cada unidade produzida, os produtos contribuem com o seguinte lucro: Produto 1, $6; Produto 2, $7; e Produto 3, $10. O tempo (em horas) que cada técnico precisa para fabricar um produto é o seguinte:
Produto
Técnico A
Técnico B
Técnico C
Técnico D
1
2
2,5
Não é possível fazer
Não é possível fazer
2
Não é possível fazer
3
Não é possível fazer
3,5
3
3
Não é possível fazer
4
Não é possível fazer
-
Cada técnico pode trabalhar até 120 horas por mês. Como o fabricante de chips pode maximizar seu lucro mensal? Suponha que um número fracionário de unidades possa ser produzido.
-
Uma fábrica de computadores produz joysticks de mouses, teclados e videogames. O lucro por unidade, o uso de mão-de-obra por unidade, a demanda mensal e o uso por unidade de tempo de máquina são dados na tabela a seguir:
Mouses
Teclados
Joysticks
Lucro/unidade
$8
US$ 11
9 dólares
Uso de mão-de-obra/unidade
.2 horas
.3 horas
.24 horas
Tempo/unidade do computador
.04 horas
.055 horas
.04 horas
Demanda mensal
15.000
27,000
11,000
-
A cada mês, um total de 13.000 horas de trabalho e 3.000 horas de tempo de máquina estão disponíveis. Como o fabricante pode maximizar sua contribuição mensal de lucro da fábrica?
-
Resolva nosso exemplo de drogas supondo que uma demanda mínima de 200 unidades para cada droga deve ser atendida.
-
Jason faz pulseiras de diamante, colares e brincos. Ele quer trabalhar no máximo 160 horas por mês. Ele tem 800 onças de diamantes. O lucro, o tempo de trabalho e as onças de diamantes necessários para produzir cada produto são dados abaixo. Se a demanda por cada produto é ilimitada, como Jason pode maximizar seu lucro?
Produto
Lucro unitário
Horas de trabalho por unidade
Onças de diamantes por unidade
Pulseira
$300
.35
1,2
Colar
$200
.15
0,75
Brincos
$100
0,05
.5










