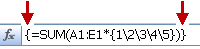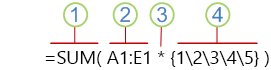Diretrizes e exemplos de fórmulas de matriz

Este exercício mostra como utilizar fórmulas de matriz de várias células e de uma célula para calcular um conjunto de números de vendas. O primeiro conjunto de passos utiliza uma fórmula de várias células para calcular um conjunto de subtotais. O segundo conjunto utiliza uma fórmula de uma célula para calcular um total geral.

• Fórmula de Matriz com várias células

  

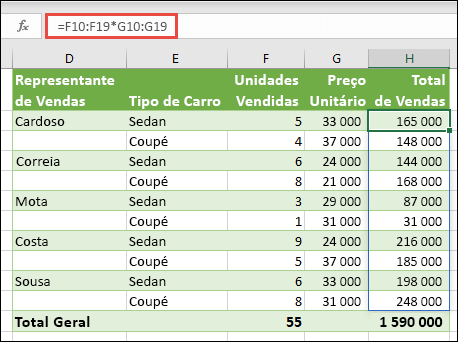
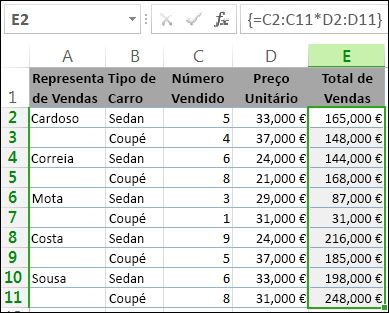
• Aqui, estamos a calcular o Total de Vendas de coupés e sedans para cada vendedor, introduzindo =F10:F19*G10:G19 na célula H10.

  Ao premir Enter, verá os resultados serem transpostos para as células H10:H19. Note que o intervalo de transposição de limites é realçado com um limite quando se seleciona qualquer célula dentro do intervalo de transposição de limites. Também se pode observar que as fórmulas nas células H10:H19 estão acinzentadas. Estão lá apenas para referência, por isso, se quiser ajustar a fórmula, terá de selecionar a célula H10, onde está a fórmula principal.

• Fórmula de matriz com uma célula

  

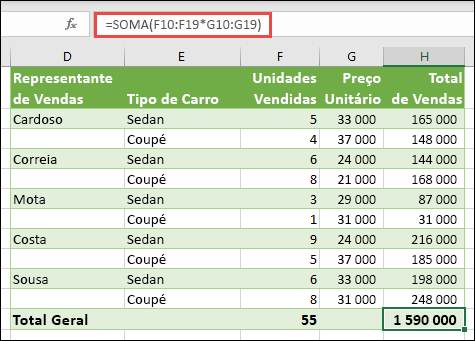
  Na célula H20 do livro de exemplo, escreva ou copie e cole =SOMA(F10:F19*G10:G19) e, em seguida, prima Enter.

  Neste caso, o Excel multiplica os valores da matriz (o intervalo de células entre F10 e G19) e, em seguida, utiliza a função SOMA para adicionar os totais. O resultado é um total geral de 1.590.000,00 € em vendas.

  Este exemplo mostra o poder deste tipo de fórmula. Por exemplo, suponhamos que tem 1000 linhas de dados. Pode somar esses dados de forma parcial ou total criando uma fórmula de matriz numa única célula em vez de arrastar a fórmula para baixo pelas 1000 linhas. Para além disso, tenha em atenção que a fórmula com uma célula (na célula H20) é completamente independente da fórmula com várias células (a fórmula nas células H10 a H19). Esta é outra vantagem subjacente à utilização de fórmulas de matriz: a flexibilidade. Pode alterar as outras fórmulas na coluna H sem afetar a fórmula na célula H20. Também pode ser uma boa prática ter totais independentes como este, uma vez que ajuda a validar a precisão dos seus resultados.

• As fórmulas de matriz dinâmica também oferecem estas vantagens:

  • Consistência    Se clicar em qualquer uma das células abaixo de H10, verá a mesma fórmula. Essa consistência pode ajudar a garantir uma maior exatidão.

  • Segurança    Não é possível substituir um componente de uma fórmula de matriz com várias células. Por exemplo, clique na célula H11 e prima Delete. O Excel não altera a saída da matriz. Para alterá-la, tem de selecionar a célula superior esquerda na matriz ou a célula H10.

  • Ficheiros de tamanho mais pequeno    Muitas vezes, é possível utilizar uma única fórmula de matriz em vez de várias fórmulas intermédias. O exemplo das vendas de automóveis que utiliza uma fórmula de matriz para calcular os resultados na coluna E. Se tivesse utilizado as fórmulas padrão como =F10*G10, F11*G11, F12*G12, etc., teria utilizado 11 fórmulas diferentes para obter os mesmos resultados. Isso não é grande coisa, mas e se tivesse milhares de linhas no total? Então pode fazer uma grande diferença.

  • Eficiência    As funções de matriz podem ser uma maneira eficiente de criar fórmulas complexas. A fórmula de matriz =SOMA(F10:F19*G10:G19) é a mesma que: =SOMA(F10*G10;F11*G11;F12*G12;F13*G13;F14*G14;F15*G15;F16*G16;F17*G17;F18*G18;F19*G19).

  • Transposição de Limites    As fórmulas de matriz dinâmica serão automaticamente transpostas para o intervalo de saída. Se os seus dados de origem estiverem numa tabela do Excel, então as fórmulas de matriz dinâmica serão automaticamente redimensionadas à medida que adiciona ou remove dados.

  • Erro de #TRANSPOSIÇÃO!    As matrizes dinâmicas introduziram o erro de #TRANSPOSIÇÃO!, o que indica que o intervalo de transposição de limites pretendido está bloqueado por algum motivo. Quando resolver o bloqueio, a fórmula será automaticamente transposta.

As constantes de matriz são um componente das fórmulas de matriz. As constantes de matriz são criadas através da introdução de uma lista de itens e, em seguida, da colocação manual da lista entre chavetas ({ }) da seguinte forma:

={1\2\3\4\5} or ={"Janeiro"\"Fevereiro"\"Março"}

Se separar os itens utilizando vírgulas, criará uma matriz horizontal (uma linha). Se separar os itens utilizando pontos e vírgulas, criará uma matriz vertical (uma coluna). Para criar uma matriz bidimensional, deverá delimitar os itens em cada linha com vírgula e delimitar cada linha com ponto e vírgula.

O procedimento que se segue dar-lhe-á alguma prática na criação de constantes horizontais, verticais e bidimensionais. Vamos mostrar exemplos com a função SEQUÊNCIA para gerar automaticamente constantes de matriz, bem como constantes de matriz introduzidas manualmente.

• Criar uma constante horizontal

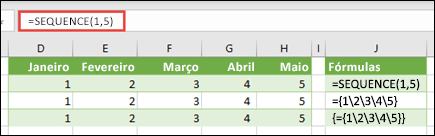
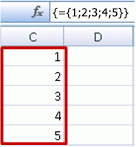
  Utilize o livro dos exemplos anteriores ou crie um novo livro. Selecione qualquer célula vazia e introduza =SEQUÊNCIA(1;5). A função SEQUÊNCIA cria uma matriz de 1 linha por 5 colunas da mesma forma que ={1\2\3\4\5}. É apresentado o seguinte resultado:

  

• Criar uma constante vertical

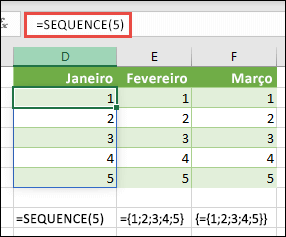
  Selecione qualquer célula em branco com espaço abaixo da célula e introduza =SEQUÊNCIA(5) ou ={1;2;3;4;5}. É apresentado o seguinte resultado:

  

• Criar uma constante bidimensional

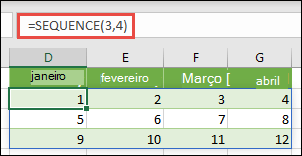
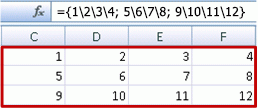
  Selecione qualquer célula em branco com espaço à direita e abaixo, e introduza =SEQUÊNCIA(3;4). Verá o seguinte resultado:

  

  Também pode introduzir: ={1\2\3\4;5\6\7\8;9\10\11\12}, mas terá de prestar atenção ao local onde coloca a vírgula ou o ponto e vírgula.

  Como pode ver, a opção SEQUÊNCIA oferece vantagens significativas em relação à entrada manual dos valores constantes da matriz. Principalmente, poupa-lhe tempo, mas também pode ajudar a reduzir os erros de entrada manual. Também é mais fácil de ler, especialmente porque um ponto e vírgula podem ser difícil de distinguir em relação aos separadores de vírgula.

Eis um exemplo que utiliza constantes de matriz como parte de uma fórmula maior. No livro de exemplo, vá para a folha de cálculo Constante numa fórmula ou crie uma nova folha de cálculo.

Na célula D9, introduzimos =SEQUÊNCIA(1;5;3;1), mas também pode introduzir 3, 4, 5, 6 e 7 nas células A9:H9. Não há nada de especial sobre essa seleção de números em particular, apenas escolhemos algo diferente de 1 a 5 para diferenciação.

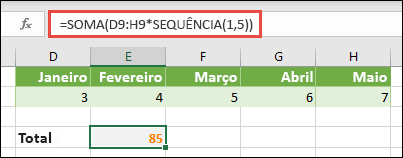
Na célula E11, introduza =SOMA(D9:H9*SEQUÊNCIA(1;5)) ou =SOMA(D9:H9*{1\2\3\4\5}). As fórmulas devolvem 85.

A função SEQUÊNCIA cria o equivalente da constante de matriz {1\2\3\4\5}. Uma vez que o Excel efetua operações sobre as expressões entre parênteses em primeiro lugar, os dois elementos seguintes a entrar em ação são os valores das células em D9:H9 e o operador de multiplicação (*). Nesse ponto, a fórmula multiplica os valores da matriz armazenada pelos valores correspondentes da constante. É o equivalente a:

=SOMA(D9*1;E9*2;F9*3;G9*4;H9*5) ou =SOMA(3*1;4*2;5*3;6*4;7*5)

Por fim, a função de SOMA adiciona os valores e devolve 85.

Para evitar utilizar a matriz armazenada e manter a operação totalmente na memória, pode substituí-la por outra constante de matriz:

=SOMA(SEQUÊNCIA(1;5;3;1)*SEQUÊNCIA(1;5)) ou =SOMA({3\4\5\6\7}*{1\2\3\4\5})

Elementos que é possível utilizar em constantes de matriz

• As constantes de matriz podem conter números, textos, valores lógicos (como VERDADEIRO e FALSO) e valores de erro tais como #N/D. Pode utilizar números em formatos inteiros, decimais e científicos. Se incluir texto, deverá colocá-lo entre aspas ("texto").

• Constantes de matriz não podem conter matrizes, fórmulas ou funções adicionais. Por outras palavras, só podem conter texto ou números separados por vírgulas ou pontos e vírgulas. O Excel mostra uma mensagem de aviso ao colocar uma fórmula como {1\2\A1:D4} ou {1\2\SOMA(Q2:Z8)}. Para além disso, valores numéricos não podem conter sinais, cifrões, vírgulas ou parênteses.

Um das melhores maneiras de usar constantes de matriz é atribuir-lhes nomes. Constantes com nomes atribuídos podem tornar-se muito mais fáceis de usar e podem omitir alguma da complexidade das fórmulas de matriz de outros. Para atribuir um nome a uma constante de matriz e usá-lo numa fórmula, faça o seguinte:

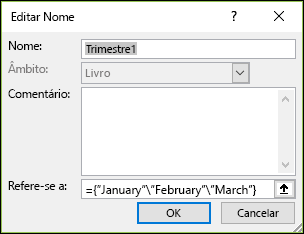
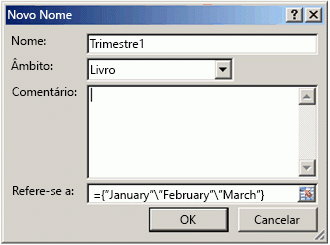
Aceda a Fórmulas > Nomes Definidos > Definir Nomes. Na caixa Nome, escreva Trimestre1. Na caixa Refere-se a, introduza a seguinte constante (não se esqueça de escrever as chavetas manualmente):

={"janeiro","fevereiro","março"}

A caixa de diálogo deverá ter o seguinte aspeto:

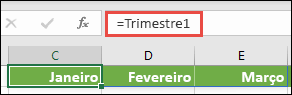
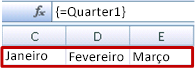
Clique OK, selecione qualquer linha com três células em branco e introduza =Trimestre1.

É apresentado o seguinte resultado:

Se quiser que os resultados sejam transpostos na vertical em vez de na horizontal, pode utilizar =TRANSPOR(Trimestre1).

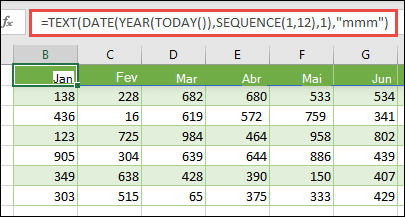
Se quiser apresentar uma lista de 12 meses, como pode utilizar ao criar um demonstrativo financeiro, pode basear uma no ano atual com a função SEQUÊNCIA. O mais interessante desta função é que, embora apenas o mês seja apresentado, existe uma data válida por trás dela que pode utilizar noutros cálculos. Encontrará estes exemplos nas folhas de cálculo Constante de matriz nomeada e no Conjunto de dados de exemplo rápido no livro de exemplo.

=TEXTO(DATA(ANO(HOJE());SEQUÊNCIA(1;12);1);"mmm")

Isto utiliza a função DATA para criar uma data com base no ano atual, a SEQUÊNCIA cria uma constante de matriz de 1 a 12 para janeiro a dezembro e, em seguida, a função TEXTO converte o formato de apresentação para "mmm" (jan, fev, mar, etc.). Se quisesse apresentar o nome completo do mês, tal como janeiro, utilizaria "mmmm".

Quando utilizar uma constante com nome como fórmula de matriz, não se esqueça de introduzir o sinal de igual, como em =Trimestre1, e não apenas Trimestre1. Se não o fizer, o Excel interpretará a matriz como sendo uma cadeia de texto e a fórmula não funcionará. Por fim, tenha em atenção que é possível utilizar combinações de funções, textos e números. Tudo depende da sua criatividade.

Os exemplos que se seguem demonstram algumas formas de utilização de constantes de matriz em fórmulas de matriz. Alguns dos exemplos utilizam a função TRANSPOR para converter linhas em colunas e vice-versa.

• Multiplicar cada item numa matriz

  Introduza =SEQUÊNCIA(1;12)*2 ou ={1\2\3\4;5\6\7\8;9\10\11\12}*2

  Também pode dividir com (/), adicionar com (+) e subtrair com (-).

• Elevar os itens de uma matriz ao quadrado

  Introduza =SEQUÊNCIA(1;12)^2 ou ={1\2\3\4;5\6\7\8;9\10\11\12}^2

• Encontrar a raiz quadrada de itens ao quadrado numa matriz

  Introduza =RAIZQ(SEQUÊNCIA(1;12)^2) ou =RAIZQ({1\2\3\4;5\6\7\8;9\10\11\12}^2)

• Transpor uma linha unidimensional

  Introduza =TRANSPOR(SEQUÊNCIA(1;5)) ou =TRANSPOR({1\2\3\4\5})

  Embora tenha introduzido uma constante de matriz horizontal, a função TRANSPOR converte a constante de matriz numa coluna.

• Transpor uma coluna unidimensional

  Introduza =TRANSPOR(SEQUÊNCIA(5;1)) ou =TRANSPOR({1;2;3;4;5})

  Embora tenha introduzido uma constante de matriz vertical, a função TRANSPOR converte a constante numa linha.

• Transpor uma constante bidimensional

  Introduza =TRANSPOR(SEQUÊNCIA(3;4)) ou =TRANSPOR({1\2\3\4;5\6\7\8;9\10\11\12})

  A função TRANSPOR converte cada linha numa série de colunas.

Esta secção oferece exemplos de fórmulas de matriz básicas.

• Criar uma matriz a partir de valores existentes

  O exemplo seguinte explica como utilizar fórmulas de matriz para criar uma nova matriz a partir de uma matriz existente.

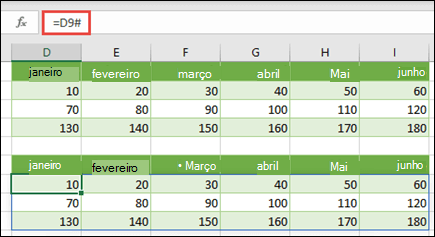
  Introduza =SEQUÊNCIA(3;6;10;10), ou ={10\20\30\40\50\60;70\80\90\100\110\120;130\140\150\160\170\180}

  Certifique-se de que introduz { (chaveta de abertura) antes de introduzir 10 e } (chaveta de fecho) depois de introduzir 180, porque está a criar uma matriz de números.

  Em seguida, =D9# ou =D9:I11 numa célula em branco. É apresentada uma matriz 3 x 6 de células com os mesmos valores que vê em D9:D11. O sinal # é denominado operador de intervalo de transposição de limites e é a forma do Excel de referenciar todo o intervalo de matriz em vez de ter de o escrever.

  

• Criar uma constante de matriz a partir de valores existentes

  Pode tirar os resultados de uma fórmula de matriz transposta e convertê-la nas partes componentes. Selecione a célula D9, depois prima F2 para mudar para o modo de edição. Em seguida, prima F9 para converter as referências das células em valores, que o Excel converte em seguida numa constante de matriz. Quando prime Enter, a fórmula =D9#, deve agora ser ={10\20\30;40\50\60;70\80\90}.

• Contar carateres num intervalo de células

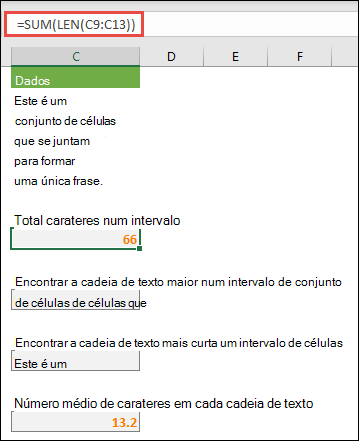
  O exemplo que se segue mostra como contar o número de carateres num intervalo de células. Isto inclui os espaços.

  

  =SOMA(NÚM.CARACT(C9:C13))

  Neste caso, a função NÚM.CARAT devolve o tamanho de cada cadeia de texto de cada uma das células do intervalo. A função SOMA soma esses valores e apresenta o resultado (66). Se quiser obter um número médio de caracteres, pode usar:

  =MÉDIA(NÚM.CARACT(C9:C13))

• Conteúdos da célula mais longa no intervalo C9:C13

  =ÍNDICE(C9:C13;CORRESP(MÁXIMO(NÚM.CARACT(C9:C13));NÚM.CARACT(C9:C13);0);1)

  Esta fórmula apenas funciona quando um intervalo de dados contém uma única coluna de células.

  Examinemos agora a fórmula, começando pelos elementos internos e trabalhando em direção ao exterior. A função NÚM.CARACT devolve o comprimento de cada um dos itens no intervalo de células D2:D6. A função MÁXIMO calcula o maior valor entre esses itens, que corresponde à cadeia de texto mais longa, que está na célula D3.

  É neste ponto que a questão fica algo complexa. A função CORRESP calcula o deslocamento (a posição relativa) da célula que contém a maior cadeia de texto. Para o fazer, requer três argumentos: um valor de pesquisa, uma matriz de pesquisa e um tipo de correspondência. A função CORRESP pesquisa na matriz de pesquisa o valor de pesquisa especificado. Neste caso, o valor de pesquisa é a maior cadeia de texto:

  MÁXIMO(NÚM.CARACT(C9:C13)

  e essa cadeia encontra-se na seguinte matriz:

  NÚM.CARACT(C9:C13)

  O argumento de tipo de correspondência neste caso é 0. O tipo de correspondência pode ser um valor de 1, 0 ou -1.

  • 1 – devolve o maior valor que seja menor ou igual ao valor de pesquisa.

  • 0 – devolve o primeiro valor que seja exatamente igual ao valor de pesquisa.

  • -1 – devolve o menor valor que seja maior ou igual ao valor de pesquisa especificado

  • Se omitir um tipo de correspondência, o Excel assumirá o valor 1.

  Por fim, a função ÍNDICE utiliza os seguintes argumentos: uma matriz e uma linha e número de coluna dentro dessa matriz. O intervalo de células C9:C13 indica a matriz, a função CORRESP indica o endereço da célula e o argumento final (1) especifica que o valor provém da primeira coluna da matriz.

  Se quisesse obter o conteúdo da menor cadeia de texto, substituiria MÁXIMO no exemplo acima por MÍNIMO.

• Encontrar os n valores menores de um intervalo

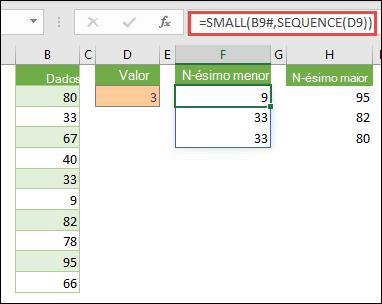
  Este exemplo mostra como encontrar os três menores valores num intervalo de células, onde foi criada uma matriz de dados de exemplo nas células B9:B18 com: =INT(MATRIZALEATÓRIA(10;1)*100). Note que MATRIZALEATÓRIA é uma função volátil, pelo que receberá um novo conjunto de números aleatórios cada vez que o Excel calcular.

  

  Enter =MENOR(B9#;SEQUENCE(D9), =MENOR(B9:B18;{1\2\3})

  Esta fórmula utiliza uma constante de matriz para avaliar a função MENOR três vezes e devolver os 3 menores membros na matriz contida nas células B9:B18, onde 3 é um valor variável na célula D9. Para encontrar mais valores, pode aumentar o valor na função SEQUÊNCIA ou adicionar mais argumentos à constante. Também pode utilizar funções adicionais com esta fórmula, como, por exemplo, SOMA ou MÉDIA. Por exemplo:

  =SOMA(MENOR(B9#;SEQUÊNCIA(D9))

  =MÉDIA(MENOR(B9#;SEQUÊNCIA(D9))

• Encontrar os n valores maiores de um intervalo

  Para encontrar os valores maiores de um intervalo, pode substituir a função MENOR pela função MAIOR. Para além disso, o exemplo que se segue utiliza as funções LIN e INDIRETO.

  Introduza =MAIOR(B9#;LIN(INDIRETO("1:3"))) ou =MAIOR(B9:B18;LIN(INDIRETO("1:3")))

  Neste momento, poderá ser útil conhecer um pouco das funções LIN e INDIRETO. Pode utilizar a função LIN para criar uma matriz de números inteiros consecutivos. Por exemplo, selecione uma célula vazia e introduza:

  =LIN(1:10)

  A fórmula cria uma coluna de 10 números inteiros consecutivos. Para ver um potencial problema, insira uma linha acima do intervalo que contém a fórmula de matriz (ou seja, acima da linha 1). O Excel ajusta as referências de linhas e a fórmula gera agora números inteiros de 2 a 11. Para corrigir esse problema, deverá adicionar a função INDIRETO à fórmula:

  =LIN(INDIRETO("1:10"))

  A função INDIRETO utiliza cadeias de texto como argumentos (motivo pelo qual o intervalo 1:10 está entre aspas). O Excel não ajusta valores de texto quando insere linhas nem move de qualquer outra forma a fórmula de matriz. Como resultado, a função LIN gera sempre a matriz de números inteiros pretendida. Pode utilizar a função SEQUÊNCIA com a mesma facilidade:

  =SEQUÊNCIA(10)

  Vamos examinar a fórmula que utilizou anteriormente — =MAIOR(B9#;LIN(INDIRETO("1:3"))) — a partir dos parênteses interiores e a trabalhar para fora: a função INDIRETO devolve um conjunto de valores de texto, neste caso os valores de 1 a 3. A função LIN, por sua vez, gera uma matriz de coluna de três células. A função MAIOR utiliza os valores no intervalo de células B9:B18 e é avaliada três vezes, uma vez para cada referência devolvida pela função LIN. Se quiser encontrar mais valores, adicione um maior intervalo de células à função INDIRETO. Por fim, como nos exemplos da função MENOR, pode utilizar esta fórmula com outras funções, como, por exemplo, SOMA e MÉDIA.

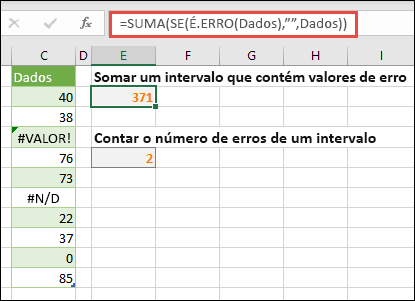
• Somar um intervalo que contém valores de erro

  A função SOMA do Excel não funciona quando tenta somar um intervalo que contém um valor de erro, como, por exemplo, #VALOR!. ou #N/D. Este exemplo mostra como somar os valores de um intervalo com o nome Dados que contém erros:

  

• =SOMA(SE(É.ERRO(Dados),"",Dados))

  A fórmula cria uma nova matriz que contém os valores originais menos os valores com erros. Começando pelas funções internas e trabalhando em direção ao exterior, a função É.ERRO procura erros no intervalo de células (Dados). A função SE devolve um valor específico se uma condição especificada devolver o valor VERDADEIRO e outro valor diferente se devolver FALSO. Neste caso, devolverá cadeias vazias ("") para todos os valores de erro, uma vez que devolvem VERDADEIRO e devolve os valores restantes do intervalo (Dados), pois devolvem FALSO, o que significa que não contêm valores de erro. A função SOMA calcula em seguida o total da matriz filtrada.

• Contar o número de valores de erro de um intervalo

  Este exemplo é como a fórmula anterior, mas devolve o número de valores de erro de um intervalo com o nome Dados em vez de os filtrar:

  =SOMA(SE(É.ERRO(Dados),1,0))

  Esta fórmula cria uma matriz que contém o valor 1 para as células que contêm erros e o valor 0 para as células que não contêm erros. É possível simplificar a fórmula e alcançar o mesmo resultado removendo o terceiro argumento da função SE da seguinte forma:

  =SOMA(SE(É.ERRO(Dados);1))

  Se não especificar o argumento, a função SE devolverá FALSO se uma célula não contiver um valor de erro. É possível simplificar ainda mais a fórmula:

  =SOMA(SE(É.ERRO(Dados)*1))

  Esta versão funciona porque VERDADEIRO*1=1 e FALSO*1=0.

Poderá necessitar de somar valores baseados em condições.

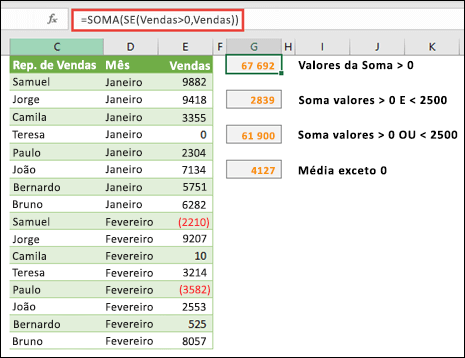
Por exemplo, esta fórmula de matriz soma apenas os números inteiros positivos de um intervalo com o nome Vendas, que representa as células E9:E24 no exemplo acima:

=SOMA(SE(Vendas>0;Vendas))

A função SE cria uma matriz de valores positivos e falsos. A função SOMA ignora essencialmente os valores falsos, pois 0+0=0. O intervalo de células utilizado nesta fórmula pode ser constituído por qualquer número de linhas e colunas.

Também pode somar valores que satisfaçam mais de uma condição. Por exemplo, esta fórmula de matriz calcula valores superiores a 0 E inferiores a 2500:

=SOMA((Vendas>0)*(Vendas<2500)*(Vendas))

Tenha em atenção que esta fórmula devolverá um erro se o intervalo contiver uma ou mais células não numéricas.

Também pode criar fórmulas de matriz que utilizem um tipo de condição OU. Por exemplo, pode somar valores superiores a 0 OU inferiores a 2500:

=SOMA(SE((Vendas>0)+(Vendas<2500);Vendas))

Não pode utilizar as funções E e OU diretamente em fórmulas de matriz, pois essas funções devolvem um único resultado (VERDADEIRO ou FALSO) e as funções de matriz requerem matrizes de resultados. Pode contornar o problema utilizando a lógica apresentada na fórmula anterior. Por outras palavras, são efetuadas operações matemáticas, como por exemplo adições ou multiplicações DE valores que satisfaçam a condição OU ou E.

Este exemplo mostra como remover zeros de um intervalo quando necessitar de calcular a média dos valores desse intervalo. A fórmula utiliza um intervalo de dados com o nome Vendas:

=MÉDIA(SE(Vendas<>0,Vendas))

A função SE cria uma matriz de valores que não sejam iguais a 0 e, em seguida, transmite esses valores para a função MÉDIA.

Esta fórmula de matriz compara os valores de dois intervalos de células com os nomes OsMeusDados e OsSeusDados e devolve o número de diferenças entre os dois. Se os conteúdos dos dois intervalos forem idênticos, a fórmula devolverá 0. Para utilizar esta fórmula, os intervalos de células têm de ter o mesmo tamanho e a mesma dimensão. Por exemplo, se OsMeusDados for um intervalo de 3 linhas por 5 colunas, OsSeusDados também têm de ter 3 linhas por 5 colunas:

=SOMA(SE(OsMeusDados=OsSeusDados;0;1))

A fórmula cria uma nova matriz com o mesmo tamanho dos intervalos que está a comparar. A função SE preenche a matriz com o valor 0 e o valor 1 (0 para incompatibilidades e 1 para células idênticas). A função SOMA devolve em seguida a soma dos valores na matriz.

É possível simplificar a fórmula do seguinte modo:

=SOMA(1*(OsMeusDados<>OsSeusDados))

À semelhança da fórmula que conta valores de erro de um intervalo, esta fórmula funciona porque VERDADEIRO*1=1 e FALSO*1=0.

Esta fórmula de matriz devolve o número de linha do valor máximo de um intervalo com uma coluna denominado Dados:

=MÍNIMO(SE(Dados=MÁXIMO(Dados),LIN(Dados),""))

A função SE cria uma nova matriz que corresponde ao intervalo denominado Dados. Se uma célula correspondente contiver o valor máximo do intervalo, a matriz conterá o número de linha. Caso contrário, a matriz conterá uma cadeia vazia (""). A função MÍNIMO utiliza a nova matriz como segundo argumento e devolve o valor mínimo, o qual corresponde ao número de linha do valor máximo de Dados. Se o intervalo denominado Dados contiver valores máximos idênticos, a fórmula devolverá a linha do primeiro valor.

Se pretender que seja devolvido o endereço de célula real de um valor máximo, utilize esta fórmula:

=ENDEREÇO(MÍNIMO(SE(Dados=MÁXIMO(Dados),LIN(Dados),"")),COL(Dados))

Encontrará exemplos semelhantes no livro de exemplo na folha de cálculo Diferenças entre conjuntos de dados.

Este exercício mostra como utilizar fórmulas de matriz de várias células e de uma célula para calcular um conjunto de números de vendas. O primeiro conjunto de passos utiliza uma fórmula de várias células para calcular um conjunto de subtotais. O segundo conjunto utiliza uma fórmula de uma célula para calcular um total geral.

• Fórmula de Matriz com várias células

Copie toda a tabela abaixo e cole dentro da célula A1 numa folha de cálculo em branco.

Representante de  Vendas	Tipo de  Carro	Número  Vendido	Preço  Unitário	Total de Vendas
Andrade	Sedan	5	33000
	Coupe	4	37000
Correia	Sedan	6	24000
	Coupe	8	21000
Neves	Sedan	3	29000
	Coupe	1	31000
Martins	Sedan	9	24000
	Coupe	5	37000
Sousa	Sedan	6	33000
	Coupe	8	31000
Fórmula (Total Geral)			Total Geral
'=SOMA(C2:C11*D2:D11)			=SOMA(C2:C11*D2:D11)

1. Para ver o Total Geral de coupés e sedans de cada vendedor, selecione as células E2:E11, introduza a fórmula =C2:C11*D2:D11 e, em seguida, prima Ctrl+Shift+Enter.

2. Para ver o Total Geral de todas as vendas, selecione a célula F11, introduza a fórmula =SOMA(C2:C11*D2:D11) e, em seguida, prima Ctrl+Shift+Enter.

Quando pressiona Ctrl+Shift+Enter, o Excel envolve a fórmula com chavetas ({ }) e insere uma instância da fórmula em cada célula do intervalo selecionado. Isto acontece de forma muito rápida e, por esta razão, o que vê na coluna E é o total de vendas de cada tipo de carro por cada vendedor. Ao selecionar E2 e, em seguida, E3, E4 e por diante, observará que é apresentada a mesma fórmula: {=C2:C11*D2:D11}. 

• Criar uma fórmula de matriz com uma célula

Na célula D13 do livro, escreva a seguinte fórmula e pressione Ctrl+Shift+Enter:

=SOMA(C2:C11*D2:D11)

Neste caso, o Excel multiplica os valores da matriz (o intervalo de células entre C2 e D11) e, em seguida, utiliza a função SOMA para adicionar os totais. O resultado é um total geral de 1.590.000,00 € em vendas. Este exemplo mostra o poder deste tipo de fórmula. Por exemplo, suponhamos que tem 1000 linhas de dados. Pode somar esses dados de forma parcial ou total criando uma fórmula de matriz numa única célula em vez de arrastar a fórmula para baixo pelas 1000 linhas.

Para além disso, tenha em atenção que a fórmula com uma célula (na célula D13) é completamente independente da fórmula com várias células (a fórmula nas células E2 a E11). Esta é outra vantagem subjacente à utilização de fórmulas de matriz: a flexibilidade. Pode alterar as fórmulas da coluna E ou eliminar essa coluna por completo sem afetar a fórmula na D13.

As fórmulas de matriz também oferecem estas vantagens:

• Consistência    Se clicar em qualquer uma das células abaixo de E2, verá a mesma fórmula. Essa consistência pode ajudar a garantir uma maior exatidão.

• Segurança    Não é possível substituir um componente de uma fórmula de matriz com várias células. Por exemplo, clique na célula E3 e prima Delete. Terá de selecionar o intervalo de células completo (E2 a E11) e alterar a fórmula para toda a matriz ou deixar a matriz tal como está. Como medida de segurança adicional, é necessário premirCtrl+Shift+Enter para confirmar qualquer alteração à fórmula.

• Ficheiros de tamanho mais pequeno    Muitas vezes, é possível utilizar uma única fórmula de matriz em vez de várias fórmulas intermédias. Por exemplo, o livro que utiliza uma fórmula de matriz para calcular os resultados na coluna E. Se tivesse utilizado fórmulas padrão (como por exemplo =C2*D2, C3*D3, C4*D4...), teria utilizado 11 fórmulas diferentes para obter os mesmos resultados.

No geral, as fórmulas de matriz utilizam uma sintaxe de fórmula padrão. Todas começam com um sinal de igual (=) e é possível utilizar a maioria das funções incorporadas do Excel nas fórmulas de matriz. A principal diferença reside no facto de, ao utilizar uma fórmula de matriz, ter de premir Ctrl+Shift+Enter para introduzir a fórmula. Ao fazê-lo, o Excel coloca a fórmula de matriz entre chavetas  - se escrever as chavetas manualmente, a fórmula será convertida numa cadeia de texto e não funcionará.

As funções de matriz podem ser uma maneira eficiente de criar fórmulas complexas. A fórmula de matriz =SOMA(C2:C11*D2:D11) é o mesmo que: =SOMA(C2*D2,C3*D3,C4*D4,C5*D5,C6*D6,C7*D7,C8*D8,C9*D9,C10*D10,C11*D11).

Sempre que trabalhar com fórmulas com várias células, lembre-se:

• Selecione o intervalo de células que irá conter os resultados antes de introduzir a fórmula. Efetuou este procedimento quando criou a fórmula de matriz de várias células quando selecionou as células E2 a E11.

• Não é possível alterar o conteúdo de uma célula individual numa fórmula de matriz. Para tentar fazê-lo, selecione a célula E3 no livro e prima DELETE. O Excel apresenta uma mensagem a indicar que não é possível alterar parte de uma matriz.

• É possível mover ou eliminar a totalidade de uma fórmula de matriz, mas não é possível mover ou eliminar parte dessa fórmula. Noutras palavras, para reduzir uma fórmula de matriz, deverá eliminar primeiro a fórmula existente e, em seguida, começar de novo.

• Para eliminar uma fórmula de matriz, selecione todo o intervalo da fórmula (por exemplo, E2:E11) e, em seguida, prima Delete.

• Não é possível inserir células em branco ou eliminar células de uma fórmula de matriz com várias células.

Por vezes, poderá ser necessário expandir uma fórmula de matriz. Selecione a primeira célula do intervalo de matriz existente e continue até selecionar todo o intervalo ao qual pretende expandir a fórmula. Prima F2 editar a fórmula, depois prima Ctrl+Shift+Enter para confirmar a fórmula depois de ajustar o intervalo da fórmula. A chave é selecionar todo o intervalo, começando pela célula superior esquerda na matriz. A célula no canto superior esquerdo é a que é editada.

As fórmulas de matriz são ótimas, mas também têm algumas desvantagens:

• Por vezes, poderá esquecer-se de premir Ctrl+Shift+Enter. Pode acontecer até aos utilizadores de Excel mais experientes. Não se esqueça de premir esta combinação de teclas sempre que introduzir ou editar uma fórmula de matriz.

• Outros utilizadores do seu livro poderão não compreender as suas fórmulas. Na prática, as fórmulas de matriz não são geralmente explicadas numa folha de cálculo. Por conseguinte, se outras pessoas precisarem de modificar os seus livros, deve evitar fórmulas de matriz ou certificar-se de que essas pessoas conhecem as fórmulas de matriz e compreendem como alterá-las, se for necessário.

• Dependendo da velocidade de processamento e da memória do computador, as fórmulas de matriz de grandes dimensões poderão diminuir a velocidade dos cálculos.

As constantes de matriz são um componente das fórmulas de matriz. As constantes de matriz são criadas através da introdução de uma lista de itens e, em seguida, da colocação manual da lista entre chavetas ({ }) da seguinte forma:

={1\2\3\4\5}

Nesta altura já sabe que tem de premir Ctrl+Shift+Enter ao criar fórmulas de matriz. Uma vez que as constantes de matriz são um componente das fórmulas de matriz, deverá colocar manualmente as constantes entre chavetas escrevendo-as. Em seguida, deverá utilizar Ctrl+Shift+Enter para introduzir toda a fórmula.

Se separar os itens utilizando vírgulas, criará uma matriz horizontal (uma linha). Se separar os itens utilizando pontos e vírgulas, criará uma matriz vertical (uma coluna). Para criar uma matriz bidimensional, deverá delimitar os itens em cada linha utilizando vírgulas e delimitar cada linha utilizando pontos e vírgulas.

Aqui está uma matriz numa única linha: {1\2\3\4}. Aqui está uma matriz numa única coluna: {1;2;3;4}. E aqui está uma matriz de duas linhas e quatro colunas: {1\2\3\4;5\6\7\8}. Na matriz de duas linhas, a primeira linha é 1, 2, 3 e 4. A segunda linha é 5, 6, 7 e 8. Um único ponto e vírgula separa as duas linhas, entre 4 e 5.

À semelhança do que acontece com as fórmulas de matriz, pode utilizar as constantes de matriz com a maioria das funções incorporada oferecida pelo Excel. As secções que se seguem explicam como criar cada tipo de constante e como utilizar essas constantes com funções do Excel.

O procedimento que se segue dar-lhe-á alguma prática na criação de constantes horizontais, verticais e bidimensionais.

Criar uma constante horizontal

1. Numa folha em branco, selecione as células A1 até E1.

2. Na barra de fórmulas, introduza a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter:

   ={1\2\3\4\5}

   Neste caso, deve escrever as chavetas de abertura e de fecho ({ }) e o Excel irá adicionar o segundo conjunto para si.

   É apresentado o seguinte resultado.

   

Criar uma constante vertical

1. No livro, selecione uma coluna com cinco células.

2. Na barra de fórmulas, introduza a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter:

   ={1;2;3;4;5}

   É apresentado o seguinte resultado.

   

Criar uma constante bidimensional

1. No livro, selecione um bloco de células com uma largura de quatro colunas e uma altura de três linhas.

2. Na barra de fórmulas, introduza a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter:

   ={1\2\3\4;5\6\7\8;9\10\11\12}

   Verá o seguinte resultado:

   

Utilizar constantes em fórmulas

Eis um exemplo simples que utiliza constantes:

1. No livro de exemplo, crie uma nova folha de cálculo.

2. Na célula A1, escreva 3 e, em seguida, escreva 4 em B1, 5 em C1, 6 em D1 e 7 em E1.

3. Na célula A3, escreva a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter:

   =SOMA(A1:E1*{1\2\3\4\5})

   Note que o Excel coloca outro conjunto de chavetas à volta da constante, dado que a introduziu como uma fórmula de matriz.

   

   O valor 85 é apresentado na célula A3.

A secção seguinte explica como funciona a fórmula.

A fórmula que acabou de utilizar contém várias partes.

1. Função

2. Matriz armazenada

3. Operador

4. Constante de matriz

O último elemento dentro dos parênteses é a constante de matriz: {1\2\3\4\5}. Lembre-se que o Excel não coloca constantes de matriz entre chavetas - terá de as escrever manualmente. Para além disso, lembre-se que após adicionar uma constante a uma fórmula de matriz, pressiona Ctrl+Shift+Enter para introduzir a fórmula.

Uma vez que o Excel efetua operações sobre as expressões entre parênteses em primeiro lugar, os dois elementos seguintes a entrar em ação são os valores armazenados no livro (A1:E1) e o operador. Nesse ponto, a fórmula multiplica os valores da matriz armazenada pelos valores correspondentes da constante. É o equivalente a:

=SOMA(A1*1,B1*2,C1*3,D1*4,E1*5)

Por fim, a função de SOMA adiciona os valores e a soma85 aparece na célula A3.

Para evitar utilizar a matriz armazenada e para manter a operação totalmente na memória, substitua a matriz armazenada por outra constante de matriz:

=SOMA({3\4\5\6\7}*{1\2\3\4\5})

Para efetuar esta operação, copie a função, selecione uma célula em branco no livro, cole a fórmula na barra de fórmulas e, em seguida, prima Ctrl+Shift+Enter. Verá o mesmo resultado que viu anteriormente no exercício que utilizava a fórmula de matriz:

=SOMA(A1:E1*{1\2\3\4\5})

Constantes de matriz podem conter números, textos, valores lógicos (como VERDADEIRO e FALSO) e valores de erro (como #N/A). Pode utilizar números de formato inteiro, decimal e científico. Se incluir texto, deverá colocar o texto entre aspas (").

Constantes de matriz não podem conter matrizes, fórmulas ou funções adicionais. Por outras palavras, só podem conter texto ou números separados por vírgulas ou pontos e vírgulas. O Excel mostra uma mensagem de aviso ao colocar uma fórmula como {1\2\A1:D4} ou {1\2\SOMA(Q2:Z8)}. Para além disso, valores numéricos não podem conter sinais, cifrões, vírgulas ou parênteses.

Possivelmente a melhor maneira de usar constantes de matriz é atribuir-lhes nomes. Constantes com nomes atribuídos podem tornar-se muito mais fáceis de usar e podem omitir alguma da complexidade das fórmulas de matriz de outros. Para atribuir um nome a uma constante de matriz e usá-lo numa fórmula, faça o seguinte:

1. No separador Fórmulas, no grupo Nomes Definidos, clique em Definir Nome.
   É apresentada a caixa de diálogo Definir Nome.

2. Na caixa Nome, escreva Trimestre1.

3. Na caixa Refere-se a, introduza a seguinte constante (não se esqueça de escrever as chavetas manualmente):

   ={"janeiro"\"fevereiro"\"março"}

   Agora, o conteúdo da caixa de diálogo tem o seguinte aspeto:

   

4. Clique OK e selecione uma linha de três células brancas.

5. Escreva a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter.

   =Trimestre1

   É apresentado o seguinte resultado.

   

Quando utilizar uma constante com nome como fórmula de matriz, não se esqueça de introduzir o sinal de igual. Se não o fizer, o Excel interpretará a matriz como sendo uma cadeia de texto e a fórmula não funcionará. Por fim, tenha em atenção que é possível utilizar combinações de texto e números.

Procure os seguintes problemas quando as constantes de matriz não funcionarem:

• Alguns elementos poderão não estar separados pelo caráter adequado. Se omitir uma vírgula ou um ponto e vírgula, ou se os colocar no local errado, a constante de matriz poderá não ser criada corretamente ou poderá ser apresentada uma mensagem de aviso.

• Poderá ter selecionado um intervalo de células que não corresponda ao número de elementos da constante. Por exemplo, se selecionar uma coluna de seis células para utilizar com uma constante de cinco células, será apresentado o valor de erro #N/A na célula vazia. Por outro lado, se selecionar células a menos, o Excel omitirá os valores que não tenham uma célula correspondente.

Os exemplos que se seguem demonstram algumas formas de utilização de constantes de matriz em fórmulas de matriz. Alguns dos exemplos utilizam a função TRANSPOR para converter linhas em colunas e vice-versa.

Multiplicar cada item numa matriz

1. Crie uma nova folha de cálculo e, em seguida, selecione um bloco de células vazias com uma largura de quatro colunas e uma altura de três linhas.

2. Escreva a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter:

   ={1\2\3\4;5\6\7\8;9\10\11\12}*2

Elevar os itens de uma matriz ao quadrado

1. Selecione um bloco de células vazias com uma largura de quatro colunas e uma altura de três linhas.

2. Escreva a seguinte fórmula de matriz e, em seguida, prima Ctrl+Shift+Enter:

   ={1\2\3\4;5\6\7\8;9\10\11\12}*{1\2\3\4;5\6\7\8;9\10\11\12}

   Em alternativa, introduza esta fórmula de matriz, que utiliza o operador de acento circunflexo (^):

   ={1\2\3\4;5\6\7\8;9\10\11\12}^2

Transpor uma linha unidimensional

1. Selecione uma coluna com cinco células em branco.

2. Escreva a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter:

   =TRANSPOR({1\2\3\4\5})

   Embora tenha introduzido uma constante de matriz horizontal, a função TRANSPOR converte a constante de matriz numa coluna.

Transpor uma coluna unidimensional

1. Selecione uma linha com cinco células em branco.

2. Introduza a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter:

   =TRANSPOR({1;2;3;4;5})

Embora tenha introduzido uma constante de matriz vertical, a função TRANSPOR converte a constante numa linha.

Transpor uma constante bidimensional

1. Selecione um bloco de células com uma largura de três colunas e uma altura de quatro linhas.

2. Introduza a seguinte constante e, em seguida, prima Ctrl+Shift+Enter:

   =TRANSPOR({1\2\3\4;5\6\7\8;9\10\11\12})

   A função TRANSPOR converte cada linha numa série de colunas.

Esta secção oferece exemplos de fórmulas de matriz básicas.

Criar matrizes e constantes de matriz a partir de valores existentes

O exemplo que se segue explica como utilizar fórmulas de matriz para criar hiperligações entre intervalos de células em diferentes folhas de cálculo. O exemplo mostra também como criar uma constante de matriz a partir do mesmo conjunto de valores.

Criar uma matriz a partir de valores existentes

1. Numa folha de cálculo no Excel, selecione as células C8:E10 e introduza esta fórmula:

   ={10\20\30;40\50\60;70\80\90}

   Certifique-se de que introduz { (chaveta de abertura) antes de introduzir 10 e } (chaveta de fecho) depois de introduzir 90, porque está a criar uma matriz de números.

2. Prima Ctrl+Shift+Enter, que introduz esta matriz de números no intervalo de células C8:E10 utilizando uma fórmula de matriz. Na sua folha de cálculo, o intervalo entre C8 e E10 têm o seguinte aspeto:

   10	20	30
   40	50	60
   70	80	90

3. Selecione o intervalo de células entre C1 e E3.

4. Introduza a seguinte fórmula na barra de fórmulas, em seguida, prima Ctrl+Shift+Enter:

   =C8:E10

   Uma matriz de células de 3x3 aparece nas células C1 a E3 com os mesmos valores se veem em C8 a E10.

Criar uma constante de matriz a partir de valores existentes

1. Com as células C1:C3 selecionadas, prima F2 para alterar para modo de edição. 

2. Prima F9 para converter as referências de células para valores. O Excel converte os valores para uma constante de matriz. A fórmula deve agora ser ={10\20\30;40\50\60;70\80\90}.

3. Prima Ctrl+Shift+Enter para introduzir a constante de matriz como fórmula de matriz.

Contar carateres num intervalo de células

O exemplo que se segue mostra como contar o número de carateres, incluindo espaços, de um intervalo de células.

1. Copie esta tabela toda e cole-a numa folha de cálculo na célula A1.

   Dados
   Isto é um
   conjunto de células
   unidas
   para formar uma
   única frase.
   Carateres totais em A2:A6
   =SOMA(NÚM.CARAT(A2:A6))
   Conteúdos da célula mais longa (A3)
   =ÍNDICE(A2:A6,CORRESP(MÁXIMO(NÚM.CARAT(A2:A6)),NÚM.CARAT(A2:A6),0),1)

2. Selecione a célula A8 e, em seguida, prima Ctrl+Shift+Enter para ver o número total de carateres nas células A2:A6 (66).

3. Selecione a célula A10 e, em seguida, prima Ctrl+Shift+Enter para ver os conteúdos da célula mais longa de todas as células A2:A6 (célula A3).

A seguinte fórmula usada na célula A8 conta o número total de carateres (66) nas células A2 a A6.

=SOMA(NÚM.CARAT(A2:A6))

Neste caso, a função NÚM.CARAT devolve o tamanho de cada cadeia de texto de cada uma das células do intervalo. A função SOMA soma os valores e apresenta o resultado (66).

Encontrar os n valores menores de um intervalo

Este exemplo mostra como encontrar os três valores menores de um intervalo de células.

1. Insira alguns números aleatórios nas células A1:A11.

2. Selecione as células C1 a C3. Este conjunto de células irá conter os resultados devolvidos pela fórmula de matriz.

3. Introduza a seguinte fórmula e, em seguida, prima Ctrl+Shift+Enter:

   =MENOR(A1:A11,{1;2;3})

Esta fórmula utiliza uma constante de matriz para avaliar a função MENOR três vezes e devolver o membro menor (1), o segundo membro menor (2) e o terceiro membro menor (3) da matriz contida nas células A1:A10. Para encontrar mais valores, adicione mais argumentos à constante. Também pode utilizar funções adicionais com esta fórmula, como, por exemplo, SOMA ou MÉDIA. Por exemplo:

=SOMA(MENOR(A1:A10,{1\2\3})

=MÉDIA(MENOR(A1:A10,{1\2\3})

Encontrar os n valores maiores de um intervalo

Para encontrar os valores maiores de um intervalo, pode substituir a função MENOR pela função MAIOR. Para além disso, o exemplo que se segue utiliza as funções LIN e INDIRETO.

1. Selecione as células D1 a D3.

2. Na barra de fórmulas, introduza esta fórmula e, em seguida, prima Ctrl+Shift+Enter:

   =MAIOR(A1:A10;LIN(INDIRETO("1:3")))

Neste momento, poderá ser útil conhecer um pouco das funções LIN e INDIRETO. Pode utilizar a função LIN para criar uma matriz de números inteiros consecutivos. Por exemplo, selecione uma coluna vazia de 10 células no seu livro, introduza esta fórmula de matriz e, em seguida, prima Ctrl+Shift+Enter:

=LIN(1:10)

A fórmula cria uma coluna de 10 números inteiros consecutivos. Para ver um potencial problema, insira uma linha acima do intervalo que contém a fórmula de matriz (ou seja, acima da linha 1). O Excel ajusta as referências de linhas e a fórmula gera números inteiros de 2 a 11. Para corrigir esse problema, deverá adicionar a função INDIRETO à fórmula:

=LIN(INDIRETO("1:10"))

A função INDIRETO utiliza cadeias de texto como argumentos (motivo pelo qual o intervalo 1:10 está entre aspas duplas). O Excel não ajusta valores de texto quando insere linhas nem move de qualquer outra forma a fórmula de matriz. Como resultado, a função LIN gera sempre a matriz de números inteiros pretendida.

Vejamos a fórmula que utilizou anteriormente — =MAIOR(A5:A14;LIN(INDIRETO("1:3"))) — a partir dos parênteses interiores e a trabalhar para fora: a função INDIRETO devolve um conjunto de valores de texto, neste caso os valores de 1 a 3. A função LINHA gera, por sua vez, uma matriz colunar de três células. A função MAIOR utiliza os valores no intervalo de células A5:A14 e é avaliada três vezes, uma vez para cada referência devolvida pela função LIN. Os valores 3200, 2700 e 2000 são devolvidos à matriz colunar de três células. Se quiser encontrar mais valores, adicione um maior intervalo de células à função INDIRETO.

Tal como nos exemplos anteriores, pode utilizar esta fórmula com outras funções, como, por exemplo, SOMA e MÉDIA.

Encontrar a cadeia de texto maior num intervalo de células

Volte ao exemplo de cadeia de texto anterior, introduza a seguinte fórmula numa célula vazia e prima Ctrl+Shift+Enter:

=ÍNDICE(A2:A6,CORRESP(MÁXIMO(NÚM.CARAT(A2:A6)),NÚM.CARAT(A2:A6),0),1)

O texto "conjunto de células que" é apresentado.

Examinemos agora a fórmula, começando pelos elementos internos e trabalhando em direção ao exterior. A função NÚM.CARACT devolve o comprimento de cada um dos itens no intervalo de células A2:A6. A função MÁXIMO calcula o maior valor entre esses itens, que corresponde à cadeia de texto mais longa, que está na célula A3.

É neste ponto que a questão fica algo complexa. A função CORRESP calcula o deslocamento (a posição relativa) da célula que contém a maior cadeia de texto. Para o fazer, requer três argumentos: um valor de pesquisa, uma matriz de pesquisa e um tipo de correspondência. A função CORRESP pesquisa na matriz de pesquisa o valor de pesquisa especificado. Neste caso, o valor de pesquisa é a maior cadeia de texto:

(MÁXIMO(NÚM.CARACT(A2:A6))

e essa cadeia encontra-se na seguinte matriz:

NÚM.CARACT(A2:A6)

O argumento do tipo de correspondência é 0. O tipo de correspondência pode ser constituído por um valor de 1, 0 ou -1. Se especificar 1, CORRESP devolverá o maior valor que seja menor ou igual ao valor de pesquisa. Se especificar 0, CORRESP devolverá o primeiro valor que seja exatamente igual ao valor de pesquisa. Se especificar -1, CORRESP encontrará o menor valor que seja maior ou igual ao valor de pesquisa especificado. Se omitir um tipo de correspondência, o Excel assumirá o valor 1.

Por fim, a função ÍNDICE utiliza os seguintes argumentos: uma matriz e uma linha e número de coluna dentro dessa matriz. O intervalo de células A2:A6 indica a matriz, a função CORRESP indica o endereço da célula e o argumento final (1) especifica que o valor provém da primeira coluna da matriz.

Esta secção oferece exemplos de fórmulas de matriz avançadas.

Somar um intervalo que contém valores de erro

A função SOMA do Excel não funciona quando tenta somar um intervalo que contém um valor de erro, como, por exemplo, #N/D. Este exemplo mostra como somar os valores de um intervalo com o nome Dados que contém erros.

=SOMA(SE(É.ERRO(Dados),"",Dados))

A fórmula cria uma nova matriz que contém os valores originais menos os valores com erros. Começando pelas funções internas e trabalhando em direção ao exterior, a função É.ERRO procura erros no intervalo de células (Dados). A função SE devolve um valor específico se uma condição especificada devolver o valor VERDADEIRO e outro valor diferente se devolver FALSO. Neste caso, devolverá cadeias vazias ("") para todos os valores de erro, uma vez que devolvem VERDADEIRO e devolve os valores restantes do intervalo (Dados), pois devolvem FALSO, o que significa que não contêm valores de erro. A função SOMA calcula em seguida o total da matriz filtrada.

Contar o número de valores de erro de um intervalo

Este exemplo é semelhante à fórmula anterior, mas devolve o número de valores de erro de um intervalo com o nome Dados em vez de os filtrar:

=SOMA(SE(É.ERRO(Dados),1,0))

Esta fórmula cria uma matriz que contém o valor 1 para as células que contêm erros e o valor 0 para as células que não contêm erros. É possível simplificar a fórmula e alcançar o mesmo resultado removendo o terceiro argumento da função SE da seguinte forma:

=SOMA(SE(É.ERRO(Dados),1))

Se não especificar o argumento, a função SE devolverá FALSO se uma célula não contiver um valor de erro. É possível simplificar ainda mais a fórmula:

=SOMA(SE(É.ERRO(Dados)*1))

Esta versão funciona porque VERDADEIRO*1=1 e FALSO*1=0.

Somar valores baseados em condições

Poderá necessitar de somar valores baseados em condições. Por exemplo, esta fórmula de matriz soma apenas os números inteiros positivos de um intervalo com o nome Vendas:

=SOMA(SE(Vendas>0,Vendas))

A função SE cria uma matriz de valores positivos e valores falsos. A função SOMA ignora essencialmente os valores falsos, pois 0+0=0. O intervalo de células utilizado nesta fórmula pode ser constituído por qualquer número de linhas e colunas.

Também pode somar valores que satisfaçam mais de uma condição. Por exemplo, esta fórmula de matriz calcula os valores maiores que 0 e menores ou iguais a 5:

=SOMA((Vendas>0)*(Vendas<=5)*(Vendas))

Tenha em atenção que esta fórmula devolverá um erro se o intervalo contiver uma ou mais células não numéricas.

Também pode criar fórmulas de matriz que utilizem um tipo de condição OU. Por exemplo, pode somar valores que sejam inferiores a 5 e superiores a 15:

=SOMA(SE((Vendas<5)+(Vendas>15),Vendas))

A função SE encontra todos os valores inferiores a 5 e superiores a 15 e, em seguida, transmite esses valores para a função SOMA.

Não pode utilizar as funções E e OU diretamente em fórmulas de matriz, pois essas funções devolvem um único resultado (VERDADEIRO ou FALSO) e as funções de matriz requerem matrizes de resultados. Pode contornar o problema utilizando a lógica apresentada na fórmula anterior. Por outras palavras, são efetuadas operações matemáticas, como por exemplo adições ou multiplicações, em valores que satisfaçam a condição OU ou E.

Calcular uma média que exclua zeros

Este exemplo mostra como remover zeros de um intervalo quando necessitar de calcular a média dos valores desse intervalo. A fórmula utiliza um intervalo de dados com o nome Vendas:

=MÉDIA(SE(Vendas<>0,Vendas))

A função SE cria uma matriz de valores que não sejam iguais a 0 e, em seguida, transmite esses valores para a função MÉDIA.

Contar o número de diferenças entre dois intervalos de células

Esta fórmula de matriz compara os valores de dois intervalos de células com os nomes OsMeusDados e OsSeusDados e devolve o número de diferenças entre os dois. Se os conteúdos dos dois intervalos forem idênticos, a fórmula devolverá 0. Para utilizar esta fórmula, os intervalos de células deverão ter o mesmo tamanho e pertencer à mesma dimensão (por exemplo, se OsMeusDados for um intervalo de 3 linhas por 5 colunas, OsSeusDados deve também ter 3 linhas por 5 colunas.

=SOMA(SE(OsMeusDados=OsSeusDados;0;1))

A fórmula cria uma nova matriz com o mesmo tamanho dos intervalos que está a comparar. A função SE preenche a matriz com o valor 0 e o valor 1 (0 para incompatibilidades e 1 para células idênticas). A função SOMA devolve em seguida a soma dos valores na matriz.

É possível simplificar a fórmula do seguinte modo:

=SOMA(1*(OsMeusDados<>OsSeusDados))

À semelhança da fórmula que conta valores de erro de um intervalo, esta fórmula funciona porque VERDADEIRO*1=1 e FALSO*1=0.

Encontrar a localização do valor máximo de um intervalo

Esta fórmula de matriz devolve o número de linha do valor máximo de um intervalo com uma coluna denominado Dados:

=MÍNIMO(SE(Dados=MÁXIMO(Dados),LIN(Dados),""))

A função SE cria uma nova matriz que corresponde ao intervalo denominado Dados. Se uma célula correspondente contiver o valor máximo do intervalo, a matriz conterá o número de linha. Caso contrário, a matriz conterá uma cadeia vazia (""). A função MÍNIMO utiliza a nova matriz como segundo argumento e devolve o valor mínimo, o qual corresponde ao número de linha do valor máximo de Dados. Se o intervalo denominado Dados contiver valores máximos idênticos, a fórmula devolverá a linha do primeiro valor.

Se pretender que seja devolvido o endereço de célula real de um valor máximo, utilize esta fórmula:

=ENDEREÇO(MÍNIMO(SE(Dados=MÁXIMO(Dados),LIN(Dados),"")),COL(Dados))