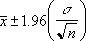ДОВЕРИТ.НОРМ (функция ДОВЕРИТ.НОРМ)

Описание

Доверительный интервал — это диапазон значений. Выборка "x" находится в центре этого диапазона, а диапазон — x ± ДОВЕРИТ.НОРМ. Например, если x — это пример времени доставки продуктов, заказаных по почте, x ± ДОВЕРИТ. НОРМ — это диапазон способов численностью населения. Для любого средней численности населения (μ0) в этом диапазоне вероятность получения выборки от μ0 больше, чем x, больше, чем альфа; для любого средней численности населения (μ0, не в этом диапазоне), вероятность получения выборки от μ0 больше, чем x, меньше, чем альфа. Другими словами, предположим, что для построения двунамерного теста на уровне значимости альфа гипотезы о том, что это μ0, используются значения x, standard_dev и размер. Тогда мы не отклонить эту гипотезу, если μ0 находится через доверительный интервал, и отклонить ее, если μ0 не находится в доверительный интервал. Доверительный интервал не позволяет нам сделать вывод о том, что вероятность 1 — альфа, что следующий пакет займет время доставки через доверительный интервал.

Синтаксис

ДОВЕРИТ.НОРМ(альфа;стандартное_откл;размер)

Аргументы функции ДОВЕРИТ.НОРМ описаны ниже.

• Альфа     — обязательный аргумент. Уровень значимости, используемый для вычисления доверительного уровня. Доверительный уровень равен 100*(1 - альфа) процентам или, иными словами, значение аргумента "альфа", равное 0,05, означает 95-процентный доверительный уровень.

• Стандартное_откл     — обязательный аргумент. Стандартное отклонение генеральной совокупности для диапазона данных, предполагается известным.

• Размер     — обязательный аргумент. Размер выборки.

Замечания

• Если какой-либо из аргументов не является числом, доверит. Норм возвращает #VALUE! значение ошибки #ЗНАЧ!.

• Если альфа ≤ 0 или альфа ≥ 1, доверит. Норм возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если standard_dev ≤ 0, доверит. Норм возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если значение аргумента "размер" не является целым числом, оно усекается.

• Если размер < 1, доверит. Норм возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если предположить, что альфа = 0,05, то нужно вычислить область под стандартной нормальной кривой, которая равна (1 - альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал определяется по формуле:

  

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.