Важно: Поддержка Office 2016 и Office 2019 была прекращена 14 октября 2025 года. Перейдите на Microsoft 365, чтобы работать удаленно с любого устройства и продолжать получать поддержку. Получить Microsoft 365
В этой статье рассматривается использование Solver, программы надстроек Microsoft Excel, с помощью которой можно использовать анализ "что если", чтобы определить оптимальное сочетание продуктов.
Как определить ежемесячный набор продуктов, который обеспечивает максимальную прибыльность?
Компаниям часто приходится определять количество каждого продукта, который будет производиться ежемесячно. В своей простейшей форме проблема ассортимента продуктов включает в себя, как определить количество каждого продукта, которое должно быть произведено в течение месяца, чтобы максимизировать прибыль. Ассортимент продуктов обычно должен соответствовать следующим ограничениям:
-
Набор продуктов не может использовать больше ресурсов, чем доступно.
-
Существует ограниченный спрос на каждый продукт. Мы не можем производить больше продукта в течение месяца, чем диктует спрос, потому что избыточное производство тратится впустую (например, скоропортящихся наркотиков).
Теперь давайте разберем следующий пример проблемы с сочетанием продуктов. Решение этой проблемы можно найти в Prodmix.xlsx файла, показанном на рис. 27.1.
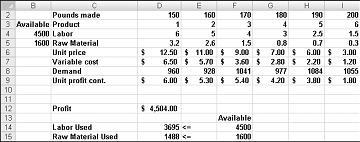
Предположим, что мы работаем на лекарственную компанию, которая производит шесть различных продуктов на своем заводе. Производство каждого продукта требует труда и сырья. В строке 4 на рис. 27-1 показаны часы труда, необходимые для производства фунта каждого продукта, а в строке 5 показаны фунты сырья, необходимые для производства фунта каждого продукта. Например, для производства фунта продукта 1 требуется шесть часов труда и 3,2 фунта сырья. Для каждого препарата цена за фунт указана в строке 6, стоимость единицы за фунт указана в строке 7, а вклад прибыли за фунт — в строке 9. Например, продукт 2 продается по цене 11,00 долл. США за фунт, стоимость единицы составляет 5,70 долл. США за фунт и обеспечивает прибыль в размере 5,30 долл. США за фунт. Потребность в каждом препарате за месяц указана в строке 8. Например, спрос на продукт 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов сырья. Как эта компания может максимизировать свою ежемесячную прибыль?
Если бы мы ничего не знали о решении Excel, мы бы атаковали эту проблему, создав лист для отслеживания прибыли и использования ресурсов, связанных с набором продуктов. Тогда мы будем использовать пробу и ошибку, чтобы изменить сочетание продуктов для оптимизации прибыли, не используя больше труда или сырья, чем доступно, и без производства каких-либо наркотиков сверх спроса. В этом процессе мы используем Средство решения только на этапе проб и ошибок. По сути, Рефер — это подсистема оптимизации, которая безупречно выполняет поиск проб и ошибок.
Ключом к решению проблемы с ассортиментом продуктов является эффективное вычисление потребления ресурсов и прибыли, связанных с любым конкретным сочетанием продуктов. Важным инструментом, который можно использовать для выполнения этого вычисления, является функция СУММПРОИЗВ. Функция СУММПРОИЗВ умножает соответствующие значения в диапазоны ячеек и возвращает сумму этих значений. Каждый диапазон ячеек, используемый в оценке СУММПРОИЗВ, должен иметь одинаковые размеры. Это означает, что можно использовать СУММПРОИЗВ с двумя строками или двумя столбцами, но не с одним столбцом и одной строкой.
В качестве примера того, как мы можем использовать функцию СУММПРОИЗВ в нашем примере набора продуктов, давайте попробуем вычислить использование ресурсов. Использование нашей рабочей силы рассчитывается по
(Труд, используемый за фунт препарата 1)*(Наркотик 1 фунт производства)+ (Труд используется за фунт препарата 2)*(Препарат 2 фунт производства) + ... (Труд, используемый за фунт препарата 6)*(Наркотик 6 фунтов производства)
Мы могли бы вычислить использование рабочей силы более утомительным способом, как D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Аналогичным образом, использование сырья может вычисляться как D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Однако ввод этих формул на лист для шести продуктов занимает много времени. Представьте, сколько времени потребуется, если бы вы работали с компанией, которая произвела, например, 50 продуктов на своем заводе. Гораздо более простой способ вычисления рабочей силы и использования сырья заключается в копировании из D14 в D15 формулы СУММПРОИЗВ($D$2:$I$2;D4:I4). Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (это наш трудозатрат), но гораздо проще ввести! Обратите внимание, что я использую знак $с диапазоном D2:I2, чтобы при копировании формулы я по-прежнему захватывал набор продуктов из строки 2. Формула в ячейке D15 вычисляет использование сырья.
Аналогичным образом, наша прибыль определяется
(Наркотик 1 прибыль на фунт)*(Препарат 1 фунт производства) + (Наркотик 2 прибыль за фунт)*(Наркотик 2 фунта произведено) + ... (Наркотик 6 прибыль за фунт)*(Препарат 6 фунтов производства)
Прибыль легко вычисляется в ячейке D12 с формулой СУММПРОИЗВ(D9:I9,$D$2:$I$2).
Теперь мы можем определить три компонента модели решения для сочетания продуктов.
-
Целевая ячейка. Наша цель — максимизировать прибыль (вычисляется в ячейке D12).
-
Изменение ячеек. Количество фунтов каждого продукта (указано в диапазоне ячеек D2:I2)
-
Ограничения целостности. У нас есть следующие ограничения:
-
Не используйте больше рабочей силы или сырья, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
-
Не производить больше препарата, чем пользуется спросом. То есть значения в клетках D2:I2 (фунты производства каждого препарата) должны быть меньше или равны потребности в каждом препарате (перечислены в клетках D8:I8).
-
Мы не можем производить отрицательное количество какого-либо препарата.
-
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в решателя. Затем все, что вам нужно сделать, это нажать кнопку Решить, чтобы найти максимально прибыльный набор продуктов!
Чтобы начать, перейдите на вкладку Данные и в группе Анализ щелкните Решатель.
Примечание: Как описано в главе 26 "Введение в оптимизацию с помощью решателя Excel", средство решения устанавливается путем нажатия кнопки Microsoft Office, затем параметров Excel, а затем надстроек. В списке Управление щелкните Надстройки Excel, проверка поле Надстройка "Решение", а затем нажмите кнопку ОК.
Откроется диалоговое окно Параметры решателя, как показано на рис. 27-2.
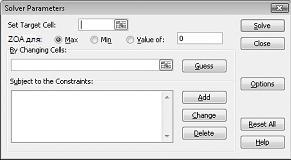
Щелкните поле Задать целевую ячейку и выберите ячейку прибыли (ячейка D12). Щелкните поле Путем изменения ячеек и укажите диапазон D2:I2, который содержит фунты, произведенные для каждого препарата. Теперь диалоговое окно должно выглядеть на рисунке 27-3.
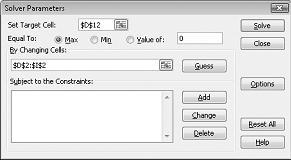
Теперь мы готовы добавить ограничения в модель. Нажмите кнопку Добавить. Откроется диалоговое окно Добавление ограничения, показанное на рис. 27-4.
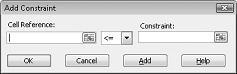
Чтобы добавить ограничения на использование ресурсов, щелкните поле Ссылка на ячейку и выберите диапазон D14:D15. Выберите <= в среднем списке. Щелкните поле Ограничение и выберите диапазон ячеек F14:F15. Диалоговое окно Добавление ограничения теперь должно выглядеть так, как рис. 27-5.
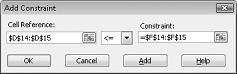
Теперь мы убедились, что при попытке решателя различных значений для изменяющихся ячеек будут рассматриваться только сочетания, удовлетворяющие как D14<=F14 (используемый труд меньше или равен трудоемкому труду) и D15<=F15 (используемое сырье меньше или равно доступному сырью). Нажмите кнопку Добавить, чтобы ввести ограничения спроса. Заполните диалоговое окно Добавление ограничения, как показано на рис. 27-6.
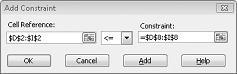
Добавление этих ограничений гарантирует, что при попытке решателя различных сочетаний для изменяющихся значений ячеек будут рассматриваться только сочетания, удовлетворяющие следующим параметрам:
-
D2<=D8 (объем производства препарата 1 меньше или равен спросу на препарат 1)
-
E2<=E8 (объем производства наркотика 2 меньше или равен спросу на наркотик 2)
-
F2<=F8 (количество произведенного препарата 3 меньше или равно спросу на препарат 3)
-
G2<=G8 (количество произведенных наркотиков 4 меньше или равно спросу на препарат 4)
-
H2<=H8 (количество произведенного препарата 5 меньше или равно спросу на препарат 5)
-
I2<=I8 (количество произведенных наркотиков 6 меньше или равно спросу на Наркотик 6)
Нажмите кнопку ОК в диалоговом окне Добавление ограничения. Окно решателя должно выглядеть так, как рис. 27-7.
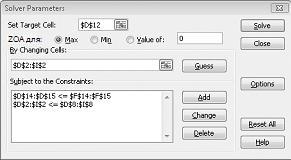
В диалоговом окне Параметры решателя мы вводим ограничение на то, что изменение ячеек не должно быть отрицательным. Нажмите кнопку Параметры в диалоговом окне Параметры решателя. Установите флажки Предполагать линейную модель и Предположить не отрицательное значение, как показано на рисунке 27-8 на следующей странице. Нажмите кнопку "ОК".
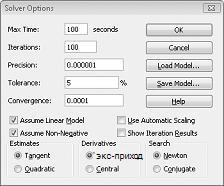
Если флажок Предположить неотрицательно, решатель рассматривает только комбинации изменяющихся ячеек, в которых каждая изменяющаяся ячейка принимает неотрицательное значение. Мы поместили флажок Предполагать линейную модель, так как проблема набора продуктов является особым типом задачи Решателя, называемой линейной моделью. По сути, модель Решателя является линейной при следующих условиях:
-
Целевая ячейка вычисляется путем сложения условий формы (изменяющаяся ячейка)*(константы).
-
Каждое ограничение удовлетворяет "линейному требованию модели". Это означает, что каждое ограничение вычисляется путем сложения условий формы (изменение ячейки)*(константы) и сравнения сумм с константой.
Почему эта задача решателя является линейной? Наша целевая ячейка (прибыль) вычисляется как
(Наркотик 1 прибыль на фунт)*(Препарат 1 фунт производства) + (Наркотик 2 прибыль за фунт)*(Наркотик 2 фунта произведено) + ... (Наркотик 6 прибыль за фунт)*(Препарат 6 фунтов производства)
Это вычисление следует шаблону, в котором значение целевой ячейки выводится путем сложения вместе терминов формы (изменение ячейки)*(константы).
Наше ограничение труда оценивается путем сравнения стоимости, полученной из (труд, используемый на фунт снадобья 1)*(Наркотик 1 фунт производства) + (Труд, используемый на фунт снадобья 2)*(Наркотик 2 фунт производства)+ ... (Труд насed за фунт снадобья 6)*(Наркотик 6 фунтов производится) для труда доступны.
Таким образом, ограничение труда оценивается путем сложения условий формы (изменение ячейки)*(константы) и сравнения сумм с константой. Ограничение трудозатрат и ограничение на сырье удовлетворяют требованиям линейной модели.
Наши ограничения спроса принимают форму
(Препарат 1 производится)<=(Спрос на наркотики 1) (Препарат 2 производится)<=(Спрос на наркотики 2) §(Препарат 6 производится)<=(Спрос на наркотики 6)
Каждое ограничение спроса также удовлетворяет требованию линейной модели, так как каждое из них вычисляется путем сложения условий формы (изменение ячейки)*(константы) и сравнения сумм с константой.
Проявив, что наша модель смешивания продуктов является линейной моделью, почему мы должны заботиться?
-
Если модель Решателя является линейной и выбран вариант Предполагать линейную модель, решатель гарантированно найдет оптимальное решение для модели Решателя. Если модель Решателя не является линейной, средство решения может найти оптимальное решение или не найти его.
-
Если модель Решателя является линейной и выбран вариант Предполагать линейную модель, решатель использует очень эффективный алгоритм (симплексный метод) для поиска оптимального решения модели. Если модель Решателя является линейной и мы не выбираем пункт Предполагать линейную модель, решатель использует очень неэффективный алгоритм (метод GRG2) и может возникнуть трудности с поиском оптимального решения модели.
После нажатия кнопки ОК в диалоговом окне Параметры решателя мы вернемся к диалоговому окою main решатель, показанное ранее на рисунке 27-7. При нажатии кнопки "Решить" решатель вычисляет оптимальное решение (если оно существует) для нашей модели набора продуктов. Как я уже говорил в главе 26, оптимальным решением модели смешения продуктов будет набор изменяющихся значений клеток (фунтов, произведенных каждого препарата), который максимизирует прибыль по сравнению с набором всех возможных решений. Опять же, приемлемым решением является набор изменяющихся значений ячеек, удовлетворяющих всем ограничениям. Изменяющиеся значения ячеек, показанные на рис. 27-9, являются приемлемым решением, так как все уровни производства не являются отрицательными, уровни производства не превышают спрос, а потребление ресурсов не превышает доступных ресурсов.
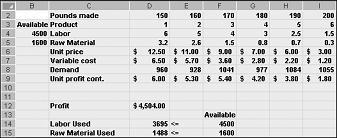
Изменяющиеся значения ячеек, показанные на рисунке 27-10 на следующей странице, представляют собой неценимое решение по следующим причинам:
-
Мы производим больше препарата 5, чем спрос на него.
-
Мы используем больше труда, чем доступно.
-
Мы используем больше сырья, чем доступно.
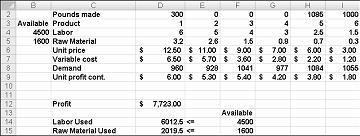
После нажатия кнопки Решить решатель быстро находит оптимальное решение, показанное на рис. 27-11. Чтобы сохранить оптимальные значения решения на листе, необходимо выбрать Сохранить решение.
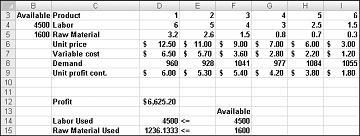
Наша лекарственная компания может максимизировать свою ежемесячную прибыль на уровне $ 6625,20 путем производства 596,67 фунтов наркотика 4, 1084 фунтов наркотиков 5, и ни одного из других наркотиков! Мы не можем определить, сможем ли мы достичь максимальной прибыли в размере $ 6625,20 другими способами. Все, что мы можем быть уверены, это то, что с нашими ограниченными ресурсами и спросом, нет способа заработать более $ 6627,20 в этом месяце.
Предположим, что спрос на каждый продукт должен быть удовлетворен. (См. лист "Нет возможного решения " в файле Prodmix.xlsx.) Затем необходимо изменить ограничения спроса с D2:I2<=D8:I8 на D2:I2>=D8:I8. Для этого откройте средство поиска, выберите ограничение D2:I2<=D8:I8 и нажмите кнопку Изменить. Откроется диалоговое окно Изменение ограничения, показанное на рис. 27-12.
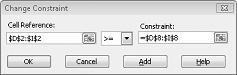
Выберите >=, а затем нажмите кнопку ОК. Теперь мы убедились, что Решатель рассмотрит возможность изменения только значений ячеек, которые соответствуют всем требованиям. При нажатии кнопки Решить отобразится сообщение "Решателям не удалось найти возможное решение". Это сообщение не означает, что мы совершили ошибку в нашей модели, а скорее, что с нашими ограниченными ресурсами мы не можем удовлетворить спрос на все продукты. Рефер просто говорит нам, что если мы хотим удовлетворить спрос на каждый продукт, мы должны добавить больше рабочей силы, больше сырья или больше обоих.
Давайте посмотрим, что произойдет, если мы допустим неограниченный спрос на каждый продукт и разрешите отрицательное количество каждого препарата. (Эта проблема с решателем отображается на листе Установка значений Не сходится в файле Prodmix.xlsx.) Чтобы найти оптимальное решение для этой ситуации, откройте Средство решения, нажмите кнопку Параметры и снимите флажок Предположить, что неотрицатель. В диалоговом окне Параметры решателя выберите ограничение спроса D2:I2<=D8:I8, а затем нажмите кнопку Удалить, чтобы удалить это ограничение. При нажатии кнопки Решить решатель возвращает сообщение "Задать значения ячеек не сходятся". Это сообщение означает, что если целевая ячейка должна быть развернута (как в нашем примере), существуют возможные решения с произвольно большими значениями целевой ячейки. (Если целевая ячейка должна быть свернута, сообщение "Задать значения ячеек не сходится" означает, что существуют возможные решения с произвольно небольшими значениями целевой ячейки.) В нашей ситуации, разрешая отрицательное производство наркотиков, мы фактически "создаем" ресурсы, которые могут быть использованы для производства произвольно большого количества других наркотиков. Учитывая наш неограниченный спрос, это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечное количество денег. Короче говоря, если отображается сообщение "Задать значения не сходится", в модели возникает ошибка.
-
Предположим, что наша лекарственная компания может приобрести до 500 часов труда на $ 1 больше в час, чем текущие затраты на рабочую силу. Как мы можем максимизировать прибыль?
-
На заводе по производству микросхем четыре техника (A, B, C и D) производят три продукта (продукты 1, 2 и 3). В этом месяце производитель микросхем может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Техник А может делать только Продукты 1 и 3. Техник Б может сделать только Продукты 1 и 2. Техник C может сделать только продукт 3. Технический специалист D может сделать только продукт 2. Для каждой произведенной единицы продукции предоставляется следующая прибыль: Продукт 1, $6; Продукт 2, $7; и Продукт 3, $10. Время (в часах), необходимое каждому техническому специалисту для производства продукта, составляет следующее:
Продукт
Техник А
Техник Б
Техник C
Техник D
1
2
2,5
Не удается сделать
Не удается сделать
2
Не удается сделать
3
Не удается сделать
3,5
3
3
Не удается сделать
4
Не удается сделать
-
Каждый техник может работать до 120 часов в месяц. Как производитель микросхем может максимизировать свою ежемесячную прибыль? Предположим, что может быть создано дробное количество единиц.
-
Завод по производству компьютеров производит мышей, клавиатуры и джойстики для видеоигр. В следующей таблице приведены сведения о прибыли на единицу, использовании рабочей силы на единицу, ежемесячном спросе и использовании на единицу машинного времени.
Мыши
Клавиатуры
Джойстики
Прибыль/единица
$8
$11
9 долл. США
Использование рабочей силы/единица
.2 часа
.3 часа
.24 часа
Машинное время или единица измерения
04 часа
.055 час
04 часа
Ежемесячный спрос
15 000
27,000
11,000
-
Каждый месяц доступно в общей сложности 13 000 рабочих часов и 3000 часов машинного времени. Как производитель может максимизировать свой ежемесячный вклад в прибыль от завода?
-
Разрешите наш пример с лекарственными средствами, предполагая, что для каждого препарата должен быть достигнут минимальный спрос в 200 единиц.
-
Джейсон делает бриллиантовые браслеты, ожерелья и серьги. Он хочет работать максимум 160 часов в месяц. У него 800 унций алмазов. Прибыль, рабочее время и унции алмазов, необходимые для производства каждого продукта, приведены ниже. Если спрос на каждый продукт неограничен, как Джейсон может максимизировать свою прибыль?
Продукт
Прибыль за единицу
Трудозатрат на единицу
Унции алмазов на единицу
Браслет
300р.
.35
1,2
Ожерелье
200 ₽
.15
.75
Серьги
100р.
0,05
.5










