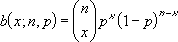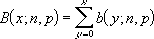Возвращает отдельное значение биномиального распределения. Функция БИНОМРАСП используется в задачах с фиксированным числом тестов или испытаний, когда результатом любого испытания может быть только успех или неудача, испытания независимы, а вероятность успеха одинакова на протяжении всего эксперимента. Например, при помощи БИНОМРАСП можно вычислить, с какой вероятностью двое из трех следующих новорожденных будут мальчиками.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция БИНОМ.РАСП.
Синтаксис
БИНОМРАСП(число_успехов;число_испытаний;вероятность_успеха;интегральная)
Аргументы функции БИНОМРАСП описаны ниже.
-
Число_успехов Обязательный. Количество успешных испытаний.
-
Число_испытаний Обязательный. Количество независимых испытаний.
-
Вероятность_успеха — обязательный аргумент. Вероятность успеха каждого испытания.
-
Интегральная Обязательный. Логическое значение, определяющее форму функции. Если кумулятив имеет значение TRUE, функция BINOMDIST возвращает функцию накопительного распределения, которая является вероятностью наличия не более number_s успехов. Если значение FALSE, возвращается функция вероятностной массы, то есть вероятность number_s успехов.
Замечания
-
Число_успехов и число_испытаний усекаются до целых.
-
Если number_s, пробных версий или probability_s не является числом, функция BINOMDIST возвращает #VALUE! (значение ошибки).
-
Если number_s < 0 или number_s > пробных версий, BINOMDIST возвращает #NUM! (значение ошибки).
-
Если probability_s < 0 или probability_s > 1, ФУНКЦИЯ BINOMDIST возвращает #NUM! (значение ошибки).
-
Если x = число_успехов, n = число_испытаний и p = вероятность_успеха, то весовая функция биномиального распределения выглядит следующим образом:
где
— ЧИСЛКОМБ(n;x).
-
Если x = число_успехов, n = число_испытаний и p = вероятность_успеха, то интегральное биномиальное распределение выглядит следующим образом:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
6 |
Количество успешных испытаний |
|
|
10 |
Количество независимых испытаний |
|
|
0,5 |
Вероятность успеха в каждом испытании |
|
|
Формула |
Описание |
Результат |
|
=БИНОМРАСП(A2;A3;A4;ЛОЖЬ) |
Вероятность того, что ровно 6 испытаний из 10 будут успешными |
0,2050781 |