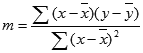LINEST (funkcia)

Popis

Funkcia LINEST vypočítava štatistiky pre určitú čiaru tak, že pomocou metódy najmenších štvorcov vypočítava priebeh priamky, ktorá najlepšie zodpovedá daným údajom, a potom vráti pole popisujúce túto priamku. Funkciu LINEST môžete skombinovať s inými funkciami a vypočítavať tak štatistiky pre iné typy modelov s lineárnymi neznámymi vrátane polynomických, logaritmických, exponenciálnych a mocninových radov. Keďže táto funkcia vráti pole hodnôt, musí byť zadaná ako vzorec poľa. Pokyny k tejto funkcii sa vzťahujú na príklady v tomto článku.

Rovnica pre výpočet tejto priamky je:

y = mx + b

alebo

y = m1x1 + m2x2 + ... + b

ak existuje viacero rozsahov hodnôt x, kde závislé hodnoty y sú funkciou nezávislých hodnôt x. Hodnoty m sú koeficienty zodpovedajúce každej hodnote x a b je konštanta. Všimnite si, že y, x a m môžu byť vektory. Pole, ktoré vráti funkcia LINEST, je {mn;mn-1,...,m1;b}. LineST môže vrátiť aj ďalšie regresné štatistiky.

Syntax

LINEST(známe_y; [známe_x]; [konštanta]; [štatistika])

Syntax funkcie LINEST obsahuje nasledovné argumenty:

Syntax

• známe_y    Povinný argument. Je to množina známych hodnôt y pre rovnicu y = mx + b.

  • Ak sa rozsah argumentu známe_y nachádza v jednom stĺpci, potom sa každý stĺpec argumentu známe_x považuje za samostatnú premennú.

  • Ak sa rozsah argumentu známe_y nachádza v jedinom riadku, potom sa každý riadok argumentu známe_x považuje za samostatnú premennú.

• známe_x    Voliteľný argument. Je to množina známych hodnôt x pre rovnicu y = mx + b.

  • Rozsah pre argument známe_x môže zahŕňať viacero množín premenných. Ak sa použije iba jedna premenná, argumenty známe_y a známe_x môžu byť rozsahy ľubovoľného tvaru, ak majú rovnaké rozmery. Ak sa použijú viaceré premenné, argument známe_y musí byť vektor (t.j. rozsah s výškou jedného riadka alebo šírkou jedného stĺpca).

  • Ak sa argument známe_x vynechá, predpokladá sa, že ide o pole {1;2;3;...} rovnakej veľkosti, akú má aj argument známe_y.

• konštanta    Voliteľný argument. Je to logická hodnota, ktorá určuje, či sa má konštanta b rovnať hodnote 0.

  • Ak je hodnota argumentu konštanta TRUE alebo nie je zadaná, konštanta b sa vypočítava normálne.

  • Ak je hodnota argumentu konštanta FALSE, konštanta b = 0 a hodnoty m sa upravia tak, aby platilo, že y = mx.

• štatistika    Voliteľný argument. Je to logická hodnota, ktorá určuje, či má funkcia vrátiť aj ďalšie regresné štatistiky.

  • Ak má štatistika hodnotu TRUE, funkcia LINEST vráti ďalšie regresné štatistiky. Výsledkom je vrátené pole {mn;mn-1,...,m1;b;sen;sen-1,...,se1;seb;r²;sey; F;df;ssreg;ssresid}.

  • Ak je hodnota argumentu štatistika FALSE alebo nie je zadaná, funkcia LINEST vráti iba koeficienty m a konštantu b.

    Ďalšie regresné štatistiky sú:

Nasledujúci príklad uvádza poradie, v ktorom sa vracajú dodatočné regresné štatistiky.

Poznámky

• Ľubovoľnú priamku môžete jednoznačne určiť pomocou smernice a priesečníka s osou y:

  Smernica (m):
  Smernicu čiary, často písanej ako m, nájdete tak, že vezmete dva body tejto čiary, (x1,y1) a (x2,y2). smernica sa rovná (y2 - y1)/(x2 - x1).

  Prieseesené y (b):
  Priesech riadka s osou y, často napísaný ako b, je hodnota y v bode, kde čiara prekríži os y.

  Rovnica priamky je y = mx + b. Keď poznáte hodnoty m a b, môžete vypočítať ľubovoľný bod v riadku tak, že do rovnice pripojíte hodnotu y alebo x. Môžete použiť aj funkciu TREND.

• Ak máte iba jedinú nezávislú premennú x, hodnoty smernice a priesečníka s osou y môžete získať priamo z nasledujúcich vzorcov:

  Smernica:
  =INDEX(LINEST(known_y;known_x;1)

  Prieseesené y:
  =INDEX(LINEST(known_y;known_x;2)

• Presnosť priamky vypočítanej funkciou LINEST závisí od miery rozptylu údajov. Čím je linearita údajov väčšia, tým je model funkcie LINEST presnejší. Funkcia LINEST používa na určenie najvhodnejšej závislosti pre údaje metódu najmenších štvorcov. Ak máte iba jednu nezávislú premennú x, hodnoty m a b sa budú počítať podľa nasledovných vzorcov:

  

  

  kde x a y sú priemerné hodnoty vzorky, t. j. x =AVERAGE(známe_x) a y = AVERAGE(známe_y).

• Funkcie LINEST a CURVE-fit dokáže vypočítať najlepšiu priamku alebo exponenciálnu krivku, ktorá vyhovuje údajom. Musíte sa však rozhodnúť, ktorý z týchto dvoch výsledkov najlepšie vyhovuje vašim údajom. Funkcia TREND(known_y;known_x) môžete vypočítať pre priamku alebo GROWTH(known_y, known_xje) pre exponenciálnu krivku. Tieto funkcie vrátia bez new_x argumentu hodnoty y predpokladané pozdĺž tejto čiary alebo krivky na aktuálnych údajových bodoch. Potom môžete porovnávať predpokladané hodnoty s aktuálnymi hodnotami. Možno ich budete chcieť vytvoriť v grafe na vizuálne porovnanie.

• V regresnej analýze Excel vypočíta pre každý bod rozdiel k štvorcovi medzi hodnotou y odhadom pre tento bod a jeho skutočnou hodnotou y. Súčet týchto druhých mocníz rozdielov sa nazýva reziduálny súčet štvorcov, ssresid. Excel vypočíta celkový súčet štvorcov, ssstotal. Ak argument básn = TRUE alebo je vynechaný, celkový súčet druhých mocnín je súčet druhých mocnín rozdielov medzi skutočnými hodnotami y a priemerom hodnôt y. Ak argument const = FALSE, celkový súčet štvorcov je súčet druhých mocnín skutočných hodnôt y (bez odčítania priemernej hodnoty y od každej jednotlivej hodnoty y). Potom možno nájsť regresný súčet štvorcov, ssreg, z: ssreg = sstotal - ssresid. Čím je reziduálny súčet štvorcov menší, v porovnaní s celkovým súčtom štvorcov, tým väčšia je hodnota určujúceho koeficientu^r2,čo je indikátor toho, ako dobre rovnica vyplývajúca z regresnej analýzy vysvetľuje vzťah medzi premennými. Hodnota r^{2 sa} rovná ssreg/sstotal.

• V niektorých prípadoch jeden alebo viacero stĺpcov X (predpokladá sa, že Y a X sú v stĺpcoch) nemusia mať v prítomnosti iných stĺpcov X ďalšiu prediktívnu hodnotu. Inými slovami, odstránenie jedného alebo viacerých stĺpcov X môže viesť k predpovedať hodnoty Y, ktoré sú rovnako presné. V tomto prípade by sa tieto nadbytočné stĺpce X mali vynechať z regresného modelu. Táto priepustnosť sa nazýva "kolinearita", pretože každý nadbytočný stĺpec X možno vyjadriť ako súčet násobkov ne redundantných stĺpcov X. Funkcia LINEST kontroluje kolinearitu a odstráni nadbytočné stĺpce X z regresného modelu, keď ich identifikuje. Odstránené stĺpce X je možné vo výstupe LINEST rozpoznať ako hodnoty s 0 koeficientmi okrem 0 se. Ak sa jeden alebo viaceré stĺpce odstránia ako nadbytočné, df bude ovplyvnené, pretože df závisí od počtu stĺpcov X použitých na predvídateľné účely. Podrobnosti o výpočte df nájdete v príklade 4. Pri zmene df z dôvodu nadbytočných stĺpcov X sa tiež odstránia hodnoty sey a F. Kolinearita by v praxi mala byť relatívne zriedkavá. Ak však niektoré stĺpce X obsahujú iba hodnoty 0 a 1 ako ukazovatele toho, či predmet experimentu je alebo nie je členom konkrétnej skupiny, je to prípad, v ktorom je pravdepodobnejšie, že ide o jeden prípad. Ak argument const = TRUE alebo sa vynechá, funkcia LINEST efektívne vloží ďalší stĺpec X všetkých 1 hodnôt na modelovanie prieseného úseku. Ak máte stĺpec s číslom 1 pre každý predmet, ak muž, alebo 0, ak nie, a máte tiež stĺpec s číslom 1 pre každú tému, ak žena, alebo 0, ak nie, tento druhý stĺpec je nadbytočný, pretože jej príspevky možno získať z odčítania záznamu v stĺpci "Mužský indikátor" od položky v druhom stĺpci všetkých 1 hodnôt pridaných funkciou LINEST.

• Ak sa z modelu neodstránia žiadne stĺpce X v dôsledku kolinearity, hodnota df sa vypočíta nasledovným spôsobom: Ak existuje počet stĺpcov k s hodnotami známe_x a argument konštanta = TRUE alebo je vynechaný, df = n – k – 1. Ak argument konštanta = FALSE, df = n – k. V oboch prípadoch každý stĺpec X, ktorý bol odstránený z dôvodu kolinearity, zvyšuje hodnotu df o 1.

• Keď zadávate ako argument konštantu poľa (ako je napríklad známe_x), hodnoty v tom istom riadku oddeľujte čiarkou a jednotlivé riadky oddeľujte bodkočiarkou. Znaky oddeľovača závisia od miestnych nastavení počítača a môžu sa odlišovať.

• Poznamenávame, že hodnoty y predpovedané regresnou rovnicou nemusia platiť, ak sú mimo oblasti hodnôt y, z ktorých ste rovnicu vytvárali.

• Algoritmus použitý vo funkcii LINEST je odlišný od algoritmu použitého vo funkciách SLOPE a INTERCEPT. V prípade neurčených a kolineárnych údajov môže rozdiel medzi týmito algoritmami viesť k odlišným výsledkom. Ak napríklad údajové body argumentu známe_y sú 0 a údajové body argumentu známe_x sú 1:

  • Funkcia LINEST vráti hodnotu 0. Algoritmus funkcie LINEST je navrhnutý tak, aby vrátil primerané výsledky pre kolineárne údaje, a v tomto prípade je možné získať najmenej jednu odpoveď.

  • Funkcie SLOPE a INTERCEPT vrátia #DIV/0! . Algoritmus funkcií SLOPE a INTERCEPT je navrhnutý tak, aby hľadať iba jednu odpoveď, a v tomto prípade môže odpovedať aj viac než jedna odpoveď.

• Okrem funkcie LOGEST môžete na výpočet štatistiky iných regresných typov použiť aj funkciu LINEST, a to tak, že zadáte funkcie premenných x a y ako rady x a y funkcie LINEST. Napríklad pomocou vzorca:

  =LINEST(hodnotyy; hodnotyx^STĹPEC($A:$C))

  v prípade, že máte jeden stĺpec hodnôt y a jeden stĺpec hodnôt x, môžete vypočítať kubickú (polynómnu tretieho rádu) aproximáciu vo forme:

  y = m1*x + m2*x^2 + m3*x^3 + b

  Úpravou tohto vzorca môžete vypočítať iné typy regresií, ale v niektorých prípadoch treba upraviť výstupné hodnoty a iné štatistiky.

• Hodnota F-testu, ktorú vracia funkcia LINEST, sa odlišuje od hodnoty F-testu, ktorú vracia funkcia FTEST. Funkcia LINEST vracia F-štatistiku, zatiaľ čo funkcia FTEST vracia pravdepodobnosť.

Príklady