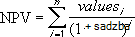NPV (funkcia)

Syntax

NPV(sadzba;hodnota1;hodnota2;...)

Sadzba     je diskontná sadzba počas jedného obdobia.

Hodnota1; hodnota2,...     sú 1 až 29 argumentmi predstavujúcimi platby a príjmy. Hodnota1; hodnota2,... musia byť rovnomerne rozmiestnené v čase a musia sa nachádzať na konci každého obdobia. NPV používa poradie hodnoty1, hodnota2,... na interpretáciu poradia hotovostných tokov. Nezabudnite zadať hodnoty platieb a príjmov v správnom poradí. Počítajú sa argumenty, ktoré sú číslami, prázdnymi, logickými hodnotami alebo textovými vyjadreniami čísel. argumenty, ktoré sú chybovými hodnotami alebo textom, ktorý nemožno preložiť na čísla, sa ignorujú.

Poznámky

• Pri funkcii NPV sa investícia začína jedno obdobie pred dňom, ktorý je vyjadrený argumentom hodnota1, a končí sa poslednou platbou v zozname. Výpočet funkcie NPV vychádza z budúcich hotovostných tokov. Ak sa prvý hotovostný tok vyskytne na začiatku prvého obdobia, táto prvá hodnota sa musí pripočítať k výsledku funkcie NPV, ale nesmie sa zahrnúť medzi argumenty. Ďalšie informácie nájdete v nasledujúcich príkladoch.

• Ak je n počet hotovostných tokov v zozname hodnôt, potom vzorec pre funkciu NPV je:

  

• NPV sa podobá na funkciu PV (súčasná hodnota). Hlavný rozdiel medzi funkciami PV a NPV spočíva v tom, že funkcia PV umožňuje začiatok toku hotovosti buď na konci, alebo na začiatku obdobia. Na rozdiel od premenlivých hodnôt toku hotovosti pri funkcii NPV musia byť toky hotovosti funkcie PV počas trvania investície konštantné. Ďalšie informácie o anuitách a finančných funkciách nájdete pri popise funkcie PV.

Príklad 1

V nasledujúcom príklade:

• Sadzba je ročná diskontná sadzba.

• Hodnota1 je počiatočná cena investície za jeden rok od dnešného dňa.

• Hodnota2 je výnos z prvého roka.

• Hodnota3 je výnos z druhého roka.

• Hodnota4 je výnos z tretieho roka.

V príklade zahrniete počiatočnú cenu 10 000 EUR ako jednu z hodnôt, pretože platba sa uskutoční na konci prvého obdobia.

Príklad 2

V nasledujúcom príklade:

• Sadzba je ročná diskontná sadzba. Môže predstavovať mieru inflácie alebo úrokovú sadzbu konkurenčnej investície.

• Hodnota1 je počiatočná cena investície za jeden rok od dnešného dňa.

• Hodnota2 je výnos z prvého roka.

• Hodnota3 je výnos z druhého roka.

• Hodnota4 je výnos z tretieho roka.

• Hodnota5 je výnos zo štvrtého roka.

• Hodnota6 je výnos z piateho roka.

V príklade nezahrniete počiatočné náklady vo výške 40 000 EUR ako jednu z hodnôt, pretože platba sa uskutoční na začiatku prvého obdobia.