Using Solver for capital budgeting

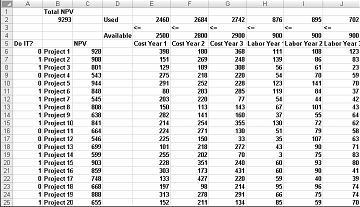
Većina korporacija želi da poduzme projekte koji doprinose najvećoj neto sadašnjoj vrednosti (NPV), podložni ograničenim resursima (obično velikim i velikim slovom). Recimo da neko preduzeće za razvoj softvera pokušava da utvrdi koji od 20 softverskih projekata treba da se shvate. NPV (u milionima dolara) doprinosi svakom projektu, kao i glavnom gradu (u milionima dolara) i broj programera koji su potrebni programerima tokom svake od sledeće tri godine dat je na radnom listu Osnovni model u datoteci Capbudget.xlsx, koja je prikazana na stranici Slika 30-1 na sledećoj stranici. Na primer, Project 2 dodelja 908 miliona USD. To zahteva 151 milion USD tokom 1. godine, 269 miliona USD tokom 2. godine i 248 miliona USD tokom 3. godine. Project 2 zahteva 139 programera tokom 1. godine, 86 programera tokom 2. godine i 83 programera tokom 3. godine. Ćelije E4:G4 pokazuju glavni grad (u milionima dolara) dostupan tokom svake od tri godine, a ćelije H4:J4 ukazuju na to koliko programera je dostupno. Na primer, tokom 1. godine je dostupno do 2,5 miliona usd, a dostupno je 900 programera.

Preduzeće mora da odluči da li treba da se poduhvati svakog projekta. Recimo da ne možemo da preuzmemo deo softverskog projekta; ako dodelimo 0,5 potrebnih resursa, na primer, imamo neradni program koji će nam doneti prihod od 0 USD!

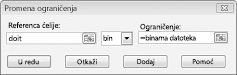
Trik u situaciji modelovanja u kojima nešto radite ili ne uradite jeste da koristite binarne promenljive ćelije. Binarna promenljiva ćelija uvek iznosi 0 ili 1. Kada binarna promenljiva ćelija koja odgovara projektu iznosi 1, mi radimo na projektu. Ako je binarna ćelija koja odgovara projektu jednaka 0, ne treba da radimo na projektu. Programski dodatak "Rešavač" podesite tako da koristi opseg binarnih ćelija tako što ćete dodati ograničenje – izaberite promenljive ćelije koje želite da koristite, a zatim odaberite stavku Bin sa liste u dijalogu Dodavanje ograničenja.

Sa ovom pozadinom, spremni smo da rešimo problem sa izborom softverskog projekta. Kao i uvek kod modela rešavača, počinjemo identifikovanjem ciljne ćelije, promenljive ćelije i ograničenja.

• Ciljna ćelija. Uvećavamo NPV generisano izabranim projektima.

• Promenljive ćelije. Potražimo 0 ili 1 binarnu promenljivu ćeliju za svaki projekat. Ove ćelije sam locirao u opsegu A6:A25 (pod imenom doit opsega). Na primer, 1 u ćeliji A6 označava da smo Project 1; a 0 u ćeliji C6 označava da ne učestvujemo Project 1.

• Ograničenja. Moramo da obezbedimo da za svaku godinu t (t=1, 2, 3), iskorišćena godina t glavnica bude manja ili jednaka godini t glavnici, a da je iskorišćeni t-godina dostupan za manje ili jednako godini t.

Kao što možete da vidite, naš radni list mora da se nadograđuje za bilo koji izbor projekata, NPV, glavni grad koji se koristi godišnje i programeri koji se koriste svake godine. U ćeliji B2 koristim formulu SUMPRODUCT(doit,NPV) da bih zbir NPV generisao izabrani projekt. (Ime opsega NPV odnosi se na opseg C6:C25.) Za svaki projekat sa 1 u koloni A ova formula pokupi NPV projekta, a za svaki projekat sa 0 u koloni A ova formula ne pokupi NPV projekta. Stoga možemo da proučimo NPV svih projekata, a ciljna ćelija je linearna zato što je ona se komprimuje sabiranjem termina koji slede obrazac (promenljive ćelije )*(konstanta). Na sličan način, procjenio sam glavni grad koji se koristi svake godine i primerak koji se koristi svake godine tako što kopiram iz E2 u F2:J2 formulu SUMPRODUCT(doit,E6:E25).

Sada popunjavam dijalog Parametri programskog sandučeta "Rešavač" kao što je prikazano u okviru "Slika 30-2".

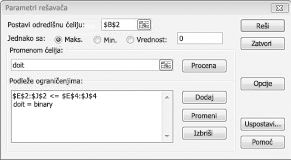
Cilj nam je da uvećamo NPV izabranih projekata (ćelija B2). Naše promenljive ćelije (opseg koji se zove "doit") jesu binarne promenljive ćelije za svaki projekat. Ograničenje E2:J2<=E4:J4 obezbeđuje da tokom svake godine glavni i iskorišćeni godišnji glavni grad bude manji od ili jednak sa velikim slovom i dostupnim laboratorijom. Da biste dodali ograničenje koje čini binarne promenljive ćelije, kliknite na dugme Dodaj u dijalogu Parametri programskog dodatka "Rešavač", a zatim sa liste u sredini dijaloga izaberite stavku Bin. Dijalog Dodavanje ograničenja bi trebalo da se pojavi kao što je prikazano u okviru "Slika 30-3".

Naš model je linearan jer se ciljna ćelija broji kao zbir termina koji imaju obrazac (promena ćelije )*( konstanta) i zbog toga što se ograničenja korišćenja resursa broje poređenjem zbira (promenljivih ćelija )*(konstanti) sa konstantom.

Kada se popuni dijalog Parametri programskog broja Solver, kliknite na dugme Reši i imamo rezultate prikazane ranije u 30-1 slikama. Preduzeće može da dobije maksimalni NPV od 9.293 miliona USD (9,293 usd) biranjem projekta 2, 3, 6–10, 14–16, 19 i 20.

Ponekad modeli za izbor projekta imaju druga ograničenja. Na primer, pretpostavimo da ako izaberemo Project 3, takođe moramo da izaberemo Project 4. Pošto je naše trenutno optimalno rešenje izabrano Project 3, a ne Project 4, znamo da trenutno rešenje ne može ostati optimalno. Da biste rešili ovaj problem, jednostavno dodajte ograničenje da je binarna promena ćelija za Project 3 manja od ili jednaka binarnim promenljivoj ćeliji Project 4.

Ovaj primer možete da pronađete na radnom listu Ako je 3, zatim 4 , u datoteci Capbudget.xlsx, koja je prikazana u 30-4. Ćelija L9 upućuje na binarnu vrednost povezanu sa ćelijom Project 3, a ćelija L12 na binarnu vrednost povezanu Project 4. Dodavanjem ograničenja L9<=L12, ako izaberemo Project 3, L9 jednako 1, a naše ograničenje primorava L12 (Project 4 binarni) da bude jednak 1. Naše ograničenje takođe mora da ostavi binarnu vrednost u promenljivoj ćelije Project 4 neograničene ako ne izaberemo Project 3. Ako ne izaberemo Project 3, L9 jednako 0, a naše ograničenje omogućava da Project 4 binarna bude jednaka 0 ili 1, što je ono što želimo. Novo optimalno rešenje prikazano je na slikama 30-4.

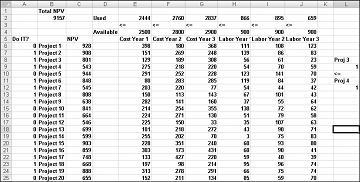
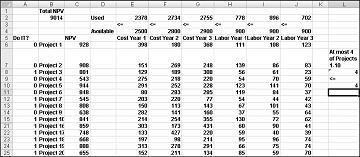
Novo optimalno rešenje se izračunava ako se izabere Project 3 znači da takođe moramo da izaberemo Project 4. Pretpostavimo da sada možemo da uradimo samo četiri projekta između 1. projekta od 1 do 10. (Pogledajte radni list Od najviše 4 od P1 do P10 , prikazan na slikama 30-5.) U ćeliji L8 zbir binarnih vrednosti povezanih sa projektima od 1 do 10 ćemo sa formulom SUM(A6:A15). Zatim dodajemo ograničenje L8<=L10, što obezbeđuje da se, u većini razloga, izabere 4 od prvih 10 projekata. Novo optimalno rešenje prikazano je na slikama 30-5. NPV je zaokupalo do 9,014 USD više od sada.

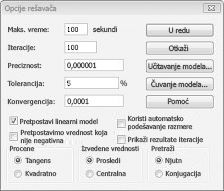
Linearni modeli rešavača u kojima su neke ili sve promenljive ćelije neophodne za binarni ili ceo broj obično se teže rešavaju od linearnih modela u kojima je svim promenljivama ćelija dozvoljeno da budu razlomci. Iz tog razloga često smo zadovoljni skoro optimalnim rešenjem za binarni ili problem sa programerima sa svim brojevima. Ako se model rešavača dugo pokreće, možda bi trebalo da razmotrite prilagođavanje postavke tolerancije u dijalogu Opcije rešavača. (Pogledajte Figure 30-6.) Na primer, postavka tolerancije od 0,5% znači da će rešavač zaustaviti kada prvi put pronađe izvodljivo rešenje koje je na 0,5 procenata od teoretički optimalne ciljne ćelije (optimalna ciljna vrednost je optimalna ciljna vrednost koja se nalazi kada se izostave binarna i celi broj ograničenja). Često smo suočeni sa izborom da pronađemo odgovor u roku od 10 procenata optimalnog za 10 minuta ili pronalaženja optimalnog rešenja za dve sedmice vremena računara! Podrazumevana vrednost tolerancije je 0,05%, što znači da se "Rešavač" zaustavlja kada pronađe vrednost ciljne ćelije na 0,05 procenata od teoretičke optimalne ciljne ćelije.

1. Preduzeće ima devet projekata koji se uzimaju u obzir. NPV koji dodaje svaki projekat i glavni grad koji je neophodan za svaki projekat u sledeće dve godine prikazuje se u sledećoj tabeli. (Svi brojevi su u milionima.) Na primer, Project 1 će dodati 14 miliona USD u NPV i zahtevati troškove od 12 miliona USD tokom 1. godine i 3 miliona USD tokom 2. godine. Tokom 1. godine za projekate je dostupno 50 miliona USD, a tokom 2. godine je dostupno 20 miliona.

	NPV	1. godina	2. godina
Project 1	14	12	3
Project 2	17	54	7
Project 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
Project 6	12	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	12	18	3

• Ako ne možemo da poduhvatmo deo projekta, ali moramo da ga iskoristimo za ceo projekat ili nijedan projekat, kako možemo da uvećamo NPV?

• Pretpostavimo da Project 4 bude u toku, Project 5 mora biti u toku. Kako možemo da uvećamo NPV?

• Preduzeće za objavljivanje pokušava da utvrdi koja od 36 knjiga treba da objavi ove godine. Datoteka u Pressdata.xlsx pruža sledeće informacije o svakoj knjizi:

  • Predviđeni prihod i troškovi razvoja (u hiljadama dolara)

  • Stranice u svakoj knjizi

  • Da li je knjiga zupčanik prema publici programera softvera (označeno brojem 1 u koloni E)

    Preduzeće za objavljivanje može da objavi knjige sa do 8500 stranica ove godine i mora da objavi najmanje četiri knjige opremene projektantima softvera. Kako preduzeće može da uveća profit?

Ovaj članak se prilagođava iz Microsoft kancelarija Excel 2007 analiza podataka i poslovnog modelinga od Veljka L. Winston.

Ovu knjigu u stilu učionice razvila je grupa prezentacija od Vene Winston, poznatog statističkog i poslovnog profesora koji je specijalizovao kreativne, praktične aplikacije Excel.