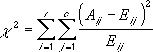Returnerar oberoendetestet. CHI2.TEST returnerar värdet från chi2-fördelningen (χ2) för statistiken och rätt frihetsgrader. Du kan använda χ2-tester för att avgöra om hypotetiska resultat kan verifieras genom ett experiment.
Syntax
CHI2.TEST(observerat_omr;förväntat_omr)
Syntaxen för funktionen CHI2.TEST har följande argument:
-
Observerat_omr Obligatoriskt. Det dataområde som innehåller observationer att testas mot förväntade värden.
-
Förväntat_omr Obligatoriskt. Det dataområde som innehåller förhållandet mellan produkten av rad- och kolumnsummor och totalsumman.
Kommentarer
-
Om observerat_omr och förväntat_omr har olika antal datapunkter returneras felvärdet #SAKNAS! av CHI2.TEST.
-
χ2-testet beräknar först en χ2-statistik med följande formel:
där:
Aij = observerad frekvens i i-raden, j-kolumnen
Eij = förväntad frekvens i i-raden, j-kolumnen
r = antalet rader
c = antalet kolumner
-
Ett lågt χ2-värde är ett tecken på oberoende. Som det framgår av formeln är χ2 alltid större än eller lika med 0, och endast 0 om Aij = Eij för alla i,j.
-
CHI2.TEST returnerar sannolikheten för att ett värde av χ2-statistik som är i alla fall lika högt som det värde som beräknas med formeln ovan kan ha uppstått av en slump under antagandet om oberoende. När den här sannolikheten beräknas använder CHI2.TEST χ2-fördelningen med ett lämpligt antal frihetsgrader (fg). Om r > 1 och c > 1, så är fg = (r - 1)(c-1). Om r = 1 och c > 1, så är fg = c - 1 eller om r > 1 och c = 1, så är fg= r - 1. r = c = 1 är inte tillåtet och #SAKNAS! returneras.
-
Användningen av CHI2.TEST fungerar bäst om Eij-värdena inte är för små. Vissa statistiker anser att Eij ska vara större än eller lika 5.
Exempel
Kopiera exempeldata i följande tabell och klistra in dem i cell A1 i ett nytt Excel-kalkylblad. När du vill att formlerna ska visa resultat markerar du dem, trycker på F2 och sedan på Retur. Om det behövs kan du justera kolumnbredderna så att alla data visas.
|
Män (Faktiskt) |
Kvinnor (Faktiskt) |
Beskrivning |
|
58 |
35 |
Instämmer |
|
11 |
25 |
Neutral |
|
10 |
23 |
Instämmer inte |
|
Män (Förväntat) |
Kvinnor (Förväntat) |
Beskrivning |
|
45,35 |
47,65 |
Instämmer |
|
17,56 |
18,44 |
Neutral |
|
16,09 |
16,91 |
Instämmer inte |
|
Formel |
Beskrivning |
Resultat |
|
=CHI2.TEST(A2:B4;A6:B8) |
χ2-statistiken för ovanstående data är 16,16957 med 2 frihetsgrader |
0,0003082 |