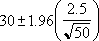Returnerar konfidensintervallet för ett populationsmedelvärde med en normal fördelning. Konfidensintervallet är ett område på vardera sidan om ett sampelmedelvärde. Om du till exempel beställer en produkt via e-post kan du med en viss förtroendenivå fastställa att den tidigaste och senaste produkten kommer.
Syntax
KONFIDENS(alfa;standard_dev;storlek)
Alfa är signifikansnivån som används för att beräkna konfidensnivån. Konfidensnivån är 100*(1 - alfa)%, eller med andra ord, ett alfa på 0,05 anger en konfidensnivå på 95 procent.
Standardavvikelse är populationens standardavvikelse för dataområdet och antas vara känd.
Storlek är exempelstorleken.
Anmärkningar
-
Om något argument inte är numeriskt returnerar KONFIDENS #VALUE! felvärdet #REFERENS!.
-
Om alfa ≤ 0 eller alfa ≥ 1 returnerar KONFIDENS #NUM! felvärdet #REFERENS!.
-
Om standard_dev ≤ 0 returnerar KONFIDENS #NUM! felvärdet #OGILTIGT!.
-
Om storlek inte är ett heltal, avkortas det.
-
Om storlek < 1 returnerar KONFIDENS #NUM! felvärdet #REFERENS!.
-
Om vi utgår från att alfa är lika med 0,05, måste vi beräkna området under standardnormalkurvan som är lika med (1 - alfa), eller 95 procent. Detta värde är ± 1.96. Konfidensintervallet är därför:
Exempel
Anta att vi observerar att i vårt urval av 50 pendlare är den genomsnittliga längden på resan till jobbet 30 minuter med en population standardavvikelse på 2,5. Vi kan vara 95 procent säkra på att populationsmedelvärdet är i intervallet:
|
Alfa |
StdddAv |
Storlek |
Formel |
Beskrivning (resultat) |
|---|---|---|---|---|
|
0,05 |
.5 |
50 |
=KONFIDENS([Alfa],[StdddAv],[Storlek]) |
Konfidensintervallet för en populations medelvärde. Med andra ord är den genomsnittliga längden på resan till arbetet 30 ± 0,692951 minuter eller 29,3 till 30,7 minuter. (0.692951) |