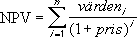Funktionen NETNUVÄRDE

Syntax

NETNUVÄRDE(ränta;värde1;värde2;...)

Ränta     är diskonteringsräntan under en period.

Värde1, värde2,...     är 1 till 29 argument som representerar betalningar och intäkter. Värde1, värde2,... måste vara jämnt fördelade i tid och ske i slutet av varje period. NETNUVÄRDE använder ordningen på värde1, värde2,... för att tolka ordningsföljden på betalningarna. Var noga med att lägga in betalningar och intäkter i rätt ordning. Argument som är tal, tomma, logiska värden eller textrepresentationer av tal räknas. argument som är felvärden eller text som inte kan översättas till tal ignoreras.

Anmärkningar

• Investeringen i NETNUVÄRDE börjar en period före datumet för betalningen i värde1 och slutar med den sista betalningen i listan. Beräkningen av NETNUVÄRDE baseras på framtida betalningar. Om den första betalningen inträffar i början av den första perioden måste det värdet adderas till resultatet av NETNUVÄRDE och inte tas med i värde-argumenten. Se följande exempel för mer information.

• Om n är antal betalningar i värde-listan så är formeln för NETNUVÄRDE:

  

• NETNUVÄRDE påminner om funktionen NUVÄRDE. Den viktigaste skillnaden mellan NUVÄRDE och NETNUVÄRDE är att NUVÄRDE tillåter betalningar att börja antingen i periodens slut eller i periodens början. Till skillnad från de varierande betalningarna i NETNUVÄRDE måste betalningarna i NUVÄRDE vara konstanta under hela investeringen. Mer information om annuiteter och finansiella funktioner finns under NUVÄRDE.

Exempel

I följande exempel:

• Ränta är den årliga diskonteringsräntan.

• Värde1 är den initiala investeringskostnaden från och med i dag.

• Värde2 är avkastningen från det första året.

• Värde3 är avkastningen från det andra året.

• Värde4 är avkastningen från tredje året.

I exemplet tar du med den ursprungliga kostnaden på 10 000 kr som ett av värdena, eftersom betalningen sker i slutet av den första perioden.

Exempel 2

I följande exempel:

• Ränta är den årliga diskonteringsräntan. Kan representera inflationsräntan eller räntesatsen för en konkurrerande investering.

• Värde1 är den initiala investeringskostnaden från och med i dag.

• Värde2 är avkastningen från det första året.

• Värde3 är avkastningen från det andra året.

• Värde4 är avkastningen från tredje året.

• Värde5 är avkastningen från det fjärde året.

• Värde6 är avkastningen från femte året.

I exemplet tar du inte med den ursprungliga kostnaden på 40 000 kr som ett av värdena, eftersom betalningen sker i början av den första perioden.