I den här artikeln beskrivs formelsyntaxen för och användningen av REGR i Microsoft Excel.
Beskrivning
Med funktionen REGR beräknas statistik för en linje genom att, med hjälp av minsta kvadratmetoden, beräkna en rät linje som bäst passar dina data, och sedan returneras en matris som beskriver linjen. Du kan även kombinera REGR med andra funktioner för att beräkna statistik för andra typer av modeller som är linjära i de okända parametrarna, inklusive polynoma, logaritmiska och exponentiella serier samt potensserier. Eftersom den här funktionen returnerar en värdematris måste den anges som en matrisformel. Instruktioner följer efter exemplen i den här artikeln.
Ekvationen för linjen är:
y = mx + b
- eller -
y = m1x1 + m2x2 + ... + b
om det finns flera områden med x-värden, där de beroende y-värdena är en funktion av de oberoende x-värdena. m-värdena är koefficienter som motsvarar varje x-värde och b är ett konstantvärde. Observera att y, x och m kan vara vektorer. Den matris som funktionen REGR returnerar är {mn;mn-1;...;m1;b}. REGR kan också returnera ytterligare regressionsstatistik.
Syntax
REGR(kända_y; [kända_x]; [konst]; [stat])
Syntaxen för funktionen REGR har följande argument:
Syntax
-
kända_y Obligatoriskt. Den mängd y-värden som är kända i förhållandet y = mx + b.
-
Om området med kända_y finns i en enskild kolumn tolkas varje kolumn i kända_x som en separat variabel.
-
Om området med kända_y finns på en enskild rad tolkas varje rad i kända_x som en separat variabel.
-
-
kända_x Valfritt. Den mängd x-värden som kan vara kända i förhållandet y = mx + b.
-
Området med known_x kan innehålla en eller flera uppsättningar variabler. Om bara en variabel används kan known_y och known_x vara områden av valfri form, så länge de har samma dimensioner. Om fler än en variabel används måste known_y vara en vektor (d.a. ett område med en rads höjd eller en kolumns bredd).
-
Om kända_x utelämnas antas argumentet vara matrisen {1;2;3;...} med samma storlek som kända_y.
-
-
konst Valfritt. Ett logiskt värde som anger om konstanten b ska vara lika med 0.
-
Om konst är SANT eller utelämnas beräknas b på normalt sätt.
-
Om konst är FALSKT, blir b lika med 0, och m-värdena justeras så att de stämmer med y = mx.
-
-
stat Valfritt. Ett logiskt värde som anger om utökad regressionsstatistik ska returneras.
-
Om statistik är SANT returnerar REGR den ytterligare regressionsstatistiken. Därför är den returnerade matrisen {mn;mn-1,...,m1;b; sen,sen-1,...,se1,seb; r2,sey; F,df; ssreg,ssresid}.
-
Om stat är FALSKT eller utelämnas returnerar REGR endast m-koefficienterna och konstanten b.
Den ytterligare regressionsstatistiken ser ut som följande.
-
|
Statistik |
Beskrivning |
|---|---|
|
se1,se2,...,sen |
Standardfelvärdena för koefficienterna m1,m2,...,mn. |
|
seb |
Standardfelvärdet för konstanten b (seb = #Saknas! när konst har värdet FALSKT). |
|
r2 |
Bestämnings koefficienten. Jämför uppskattade och faktiska y-värden och intervall i värde från 0 till 1. Om det är 1 finns det en perfekt korrelation i provet – det finns ingen skillnad mellan det uppskattade y-värdet och det faktiska y-värdet. Vid den andra extrem, om koefficienten för bestämning är 0, är regressionsekvationen inte användbar för att förutsäga ett y-värde. Mer information om hurär 2 beräknas finns i Kommentarer längre fram i det här avsnittet. |
|
sey |
Standardfelet för y-uppskattningen. |
|
f |
F-statistiken eller det observerade F-värdet. Använd F-statistiken för att avgöra om den observerade relationen mellan de beroende och de oberoende variablerna är slumpmässig. |
|
df |
Frihetsgrader. Använd frihetsgrader för att hitta F-kritiska värden i en statistiskt tabell. Jämför värdena som du hittar i tabellen med den F-statistik som returneras av REGR för att avgöra en konfidensnivå för modellen. Mer information om hur df beräknas finns i Kommentarer senare i det här avsnittet. I Exempel 4 visas hur F och df används. |
|
ssreg |
Regressionssumman av kvadrater. |
|
ssresid |
Restsumman av kvadrater. Mer information om hur ssreg och ssresid beräknas finns i Kommentarer senare i det här avsnittet. |
I följande bild visas i vilken ordning den ytterligare regressionsstatistiken returneras.

Anmärkningar
-
Du kan beskriva vilken rät linje som helst med lutningen och y-skärningspunkten:
Lutning (m):
För att hitta lutningen på en linje, ofta skriven som m, tar du två punkter på linjen, (x1,y1) och (x2,y2); lutningen är lika med (y2 - y1)/(x2 - x1).Y-skärningspunkt (b):
Y-skärningspunkten för en linje, som ofta skrivs som b, är värdet på y vid den punkt där linjen korsar y-axeln.Ekvationen för en rät linje är y = mx + b. När du känner till värdena för m och b kan du beräkna vilken punkt som helst på linjen genom att sätta in y- eller x-värdet i ekvationen. Du kan även använda funktionen TREND.
-
När du bara har en oberoende x-variabel, kan du ta reda på värdena för lutningen och y-skärningspunkten direkt med följande formler:
Backe:
=INDEX(REGR(known_y;known_x);1)Y-skärningspunkt:
=INDEX(REGR(known_y;known_x);2) -
Exaktheten för den linje som beräknas med funktionen REGR beror på spridningen av data. Ju mer linjära data, desto exaktare är REGR -modellen. REGR använder minsta kvadratmetoden för att avgöra den bästa passningen för data. När du bara har en oberoende x-variabel bygger beräkningarna för m och b på följande formler:
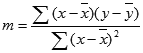
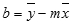
där x och y är sampelmedelvärden, alltså x = MEDEL(kända_x) och y = MEDEL(kända_y).
-
Linje- och kurvpassningsfunktionerna REGR och EXPREGR kan beräkna den bästa raka linje- eller exponentiella kurvan som passar dina data. Du måste dock bestämma vilket av de två resultaten som bäst passar dina data. Du kan beräkna TREND(known_y,known_x) för en rak linje eller EXPTREND(known_y, known_x) för en exponentiell kurva. Dessa funktioner returnerar, utan new_x argument, en matris med y-värden som förutsägs längs den linjen eller kurvan vid dina faktiska datapunkter. Sedan kan du jämföra de förväntade värdena med de faktiska värdena. Du kanske vill göra diagram med dem båda för en visuell jämförelse.
-
Vid regressionsanalys beräknas kvadraten på skillnaden mellan det uppskattade y-värdet för varje punkt och det verkliga y-värdet. Summan av kvadraten på skillnaden kallas den kvadratiska restsumman, ssresid. Därefter beräknas totalsumman av kvadraterna, sstotal. Om argumentet konst = SANT eller har utelämnats, är totalsumman summan av de kvadrerade skillnaderna mellan de verkliga y-värdena och medelvärdet av y-värdena. Om argumentet konst = FALSKT är totalsumman kvadratsumman av de verkliga y-värdena (utan att medelvärdet dras från varje y-värde). Regressionskvadratsumman ssreg ges av ssreg = sstotal - ssresid. Ju mindre restsumman av kvadrater är, jämfört med den totala summan av kvadrater, desto större är bestämningssamfficientens värde, r2, vilket är en indikator på hur väl ekvationen som följer av regressionsanalysen förklarar förhållandet mellan variablerna. Värdet på r2 är lika med ssreg/sstotal.
-
I vissa fall kan en eller flera av x-kolumnerna (om x- och y-värden är ordnade i kolumner) sakna ytterligare förutsägelsevärden i förhållande till övriga x-kolumner. En eliminering av en eller flera x-kolumner kan alltså leda till förutsagda y-värden som är lika riktiga. I detta fall bör de överflödiga x-kolumnerna uteslutas från regressionsanalysen. Fenomenet kallas "kolinjäritet" eftersom de redundanta x-kolumnerna kan uttryckas som en linjär kombination av de icke-redundanta x-kolumnerna. Funktionen REGR reagerar på kolinjäritet och tar bort alla redundanta x-kolumner från regressionsanalysen när funktionen stöter på dem. Borttagna x-kolumner kan identifieras i REGR-utdata genom att de har 0 koefficienter och dessutom 0 se-värden. Om en eller flera kolumner utesluts som redundanta påverkas df, eftersom df är beroende av det antal x-kolumner som faktiskt används i förutsägelsesyfte. Information om beräkning av df finns i Exempel 4. Om df förändras på grund av att redundanta x-kolumner utesluts, kommer värdet på sey och F också att påverkas. Kolinjäritet bör vara ganska ovanligt i verkliga sammanhang. Ett möjligt scenario är emellertid när vissa x-kolumner endast innehåller värdena 0 och 1 som indikatorer på om en deltagare i en undersökning ingår i en viss grupp eller inte. Om konst = SANT eller har utelämnats, infogar funktionen REGR en extra x-kolumn med alla 1-värden för att skapa en modell av skärningspunkten. Om du har en kolumn där 1 anger att deltagaren är en man och 0 att deltagaren inte är det, och du samtidigt har en kolumn där 1 anger att deltagaren är en kvinna och 0 att deltagaren inte är det, blir denna senare kolumn redundant eftersom posterna i den kan fås genom att posten i kolumnen med indikering av män subtraheras från posten i den extra kolumnen med alla 1-värden som läggs till en funktionen REGR.
-
Om inga x-kolumner utesluts från modellen på grund av kolinjäritet beräknas df på följande sätt: om det finns kkolumner med kända_x och konst = SANT eller har utelämnats, är df = n - k - 1. Om konst = FALSKT är df = n - k. I båda fallen kommer varje utesluten x-kolumn att öka df med 1.
-
När du anger en matriskonstant (t.ex. known_x) som argument använder du kommatecken för att avgränsa värden som finns på samma rad och semikolon för att separera rader. Avgränsningstecknet kan variera, beroende på de nationella inställningarna.
-
Observera att y-värdena som förutsägs av regressionsekvationen kanske inte är giltiga om de går utanför det intervall med y-värden som du använde för att beräkna ekvationen.
-
Den underliggande algoritmen som används i funktionen REGR är inte densamma som den underliggande algoritm som används i funktionerna LUTNING och SKÄRNINGSPUNKT. Skillnaden mellan dessa algoritmer kan innebära olika resultat vid obestämbara och kolinjära data. Till exempel, datapunkterna för argumentet kända_y är 0 och datapunkterna för argumentet kända_x är 1:
-
REGR returnerar värdet 0. Algoritmen för funktionen REGR har utformats för att returnera rimliga resultat för kolinjära data och i det här exemplet finns det minst ett svar.
-
LUTNING och SKÄRNINGSPUNKT returnerar en #DIV/0! #REF!. Algoritmen för funktionerna LUTNING och SKÄRNINGSPUNKT är utformad för att bara söka efter ett svar, och i det här fallet kan det finnas fler än ett svar.
-
-
Förutom att använda EXPREGR för att beräkna statistik för andra regressionstyper, kan du använda REGR för att beräkna en rad andra regressionstyper genom att ange funktioner för x- och y-variablerna som x- och y-serier för REGR. Till exempel fungerar följande formel:
=REGR(yvärden, xvärden^KOLUMN($A:$C))
när du har en enstaka kolumn med y-värden och en enstaka kolumn med x-värden för att beräkna kubapproximeringen (polynom för ordning 3) för formen:
y = m1*x + m2*x^2 + m3*x^3 + b
Du kan justera den här formeln för att beräkna andra typer av regression, men i vissa fall krävs en justering av utdatavärdena och annan statistik.
-
Det F-testvärde som returneras av funktionen REGR skiljer sig från det F-testvärde som returneras av funktionen FTEST. REGR returnerar F-statistiken medan FTEST returnerar sannolikheten.
Exempel
Exempel 1: Lutning och y-skärningspunkt
Kopiera exempeldata i följande tabell och klistra in dem i cell A1 i ett nytt Excel-kalkylblad. När du vill att formlerna ska visa resultat markerar du dem, trycker på F2 och sedan på Retur. Om det behövs kan du justera kolumnbredderna så att alla data visas.
|
Känt y-värde |
Känt x-värde |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Resultat (lutning) |
Resultat (y-skärningspunkt) |
|
2 |
1 |
|
Formel (matrisformel i cellerna A7:B7) |
|
|
=REGR(A2:A5;B2:B5;;FALSKT) |
Exempel 2: Enkel linjär regression
Kopiera exempeldata i följande tabell och klistra in dem i cell A1 i ett nytt Excel-kalkylblad. När du vill att formlerna ska visa resultat markerar du dem, trycker på F2 och sedan på Retur. Om det behövs kan du justera kolumnbredderna så att alla data visas.
|
Månad |
Försäljning |
|---|---|
|
1 |
3 100 kr |
|
2 |
4 500 kr |
|
3 |
4 400 kr |
|
4 |
5 400 kr |
|
5 |
7 500 kr |
|
6 |
8 100 kr |
|
Formel |
Resultat |
|
=SUMMA(REGR(B1:B6; A1:A6)*{9;1}) |
110 000 kr |
|
Gör en uppskattning av försäljningen den 9:e månaden, baserat på försäljningen under månaderna 1 till och med 6. |
Exempel 3: Multipel linjär regression
Kopiera exempeldata i följande tabell och klistra in dem i cell A1 i ett nytt Excel-kalkylblad. När du vill att formlerna ska visa resultat markerar du dem, trycker på F2 och sedan på Retur. Om det behövs kan du ändra kolumnbredden så att alla data visas.
|
Golvyta (x1) |
Kontor (x2) |
Ingångar (x3) |
Ålder (x4) |
Taxeringsvärde (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
1 420 000 kr |
|
2333 |
2 |
2 |
1,2 |
1 440 000 kr |
|
2356 |
3 |
1,5 |
33 |
1 510 000 kr |
|
2379 |
3 |
2 |
43 |
1 500 000 kr |
|
2402 |
2 |
3 |
53 |
1 390 000 kr |
|
2425 |
4 |
2 |
23 |
1 690 000 kr |
|
2448 |
2 |
1,5 |
99 |
1 260 000 kr |
|
2471 |
2 |
2 |
34 |
1 429 000 kr |
|
2494 |
3 |
3 |
23 |
1 630 000 kr |
|
2517 |
4 |
4 |
55 |
1 690 000 kr |
|
2540 |
2 |
3 |
22 |
1 490 000 kr |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Formel (dynamisk matrisformel som anges i A19) |
||||
|
=REGR(E2:E12;A2:D12;SANT;SANT) |
Exempel 4 – Använda statistik för F och r2
I föregående exempel är bestämnings koefficienten, eller r2, 0,99675 (se cell A17 i resultatet för REGR), vilket indikerar ett starkt samband mellan de oberoende variablerna och försäljningspriset. Använd F-statistik för att avgöra om resultaten med detta höga r2-värde uppstod av en slump.
Anta att det inte finns något samband mellan variablerna och att samplet med de 11 kontorsbyggnaderna inte var representativt, men att du har fått den statistiska analysen att visa ett samband. Risken för den felaktiga slutsatsen att det finns ett samband kallas Alfa.
F- och df-värdena i utdata från funktionen REGR kan användas för att bedöma sannolikheten för att ett högre F-värde inträffar av en slump. F kan jämföras med kritiska värden i publicerade F-fördelningstabeller eller så kan funktionen FFÖRD i Excel användas för att beräkna sannolikheten för att ett större F-värde ska inträffa av en slump. Lämplig F-fördelning har v1 och v2 frihetsgrader. Om n är antalet datapunkter och konst = SANT eller utelämnat, så är v1 = n – df – 1 och v2 = df. (Om konst = FALSKT, v1 = n – df och v2 = df.) Funktionen FFÖRD , med syntaxen F,v1,v2, returnerar sannolikheten för att ett högre F-värde inträffar av en slump. I det här exemplet är df = 6 (cell B18) och F = 459,753674 (cell A18).
Om vi antar att alfa-värdet är 0,05 är v1 = 11 - 6 - 1 = 4 och v2 = 6, är den kritiska F-nivån 4,53. Eftersom F = 459,753674 är väsentligt högre än 4,53, är det ytterst osannolikt att ett så högt F-värde är en slumphändelse. (Om alfa = 0,05 måste hypotesen att det inte finns något samband mellan kända_y och kända_x förkastas när F når den kritiska nivån 4,53.) Du kan använda funktionen FFÖRD i Excel för att beräkna sannolikheten för att ett så högt F-värde är en slumphändelse. Exempelvis FFÖRD(459,753674; 4; 6) = 1,37E-7, vilket är en extremt låg sannolikhet. Du kan dra slutsatsen, antingen genom att leta reda på den kritiska F-nivån i en tabell eller genom att använda funktionen FFÖRD i Excel, att regressionsekvationen är användbar för att förutsäga värdet på kontorsbyggnader i det här området. Kom ihåg att du måste använda korrekta värden på v1 och v2 enligt beräkningarna i föregående stycke.
Exempel 5: Beräkna t-statistik
Ett annat hypotestest som avgör om varje lutningskoefficient är användbar för att uppskatta värdet på en kontorsbyggnad finns i Exempel 3. Om du t.ex. vill testa ålderskoefficientens statistiska signifikans dividerar du -234,24 (ålderslutningskoefficienten) med 13,268 (det uppskattade standardfelet för ålderskoefficienter i cell A15). Följande är det t-observerade värdet:
t = m4 / se4 = -234,24/13,268 = -17,7
Om absolutvärdet på t är tillräckligt högt, kan lutningskoefficienten användas för att uppskatta värdet på en kontorsbyggnad i Exempel 3. I följande tabell finns absolutvärdena för de fyra t-observerade värdena.
Om du använder en tabell i en statistisk handbok kommer du att se att t-kritiskt, tvåsidigt, med 6 frihetsgrader och Alfa = 0,05 har värdet 2,447. Du kan hitta det kritiska värdet med hjälp av funktionen TINV i Excel. TINV(0,05;6) = 2,447. Eftersom det absoluta t-värdet 17,7 är högre än 2,447, är ålder en viktig variabel när värdet på en kontorsbyggnad ska uppskattas. På samma sätt kan den statistiska signifikansen i var och en av de övriga oberoende variablerna testas. De observerade t-värdena för var och en av de oberoende variablerna är:
|
Variabel |
t-observerat värde |
|---|---|
|
Golvyta |
5,1 |
|
Antal kontor |
31,3 |
|
Antal ingångar |
4,8 |
|
Ålder |
17,7 |
De här värdena har alla ett absolut värde som är större än 2,447, vilket innebär att alla variabler som används i regressionsekvationen är användbara vid uppskattning av taxeringsvärde på kontorsbyggnader i detta område.










