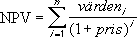I den här artikeln beskrivs formelsyntaxen för och användningen av NETNUVÄRDE i Microsoft Excel.
Beskrivning
Beräknar nuvärdet av en investering genom att använda en räntesats och en serie framtida betalningar (negativa värden) och intäkter (positiva värden).
Syntax
NETNUVÄRDE(ränta;värde1;[värde2];...)
Syntaxen för funktionen NETNUVÄRDE har följande argument:
-
Ränta Obligatoriskt. Detta är räntesatsen per period.
-
Värde1;värde2;... Värde1 är obligatoriskt, alla efterföljande värden är valfria. Detta är de 1 till 254 argument som motsvarar betalningar och intäkter.
-
Värde1;värde2;... måste ske med lika stora tidsintervall och förekomma i slutet av varje period.
-
NETNUVÄRDE använder ordningen på värde1; värde2; ... för att tolka ordningsföljden på betalningarna. Var noga med att lägga in betalningar och intäkter i rätt ordning.
-
Argument som är tomma celler, logiska värden eller textrepresentationer av tal, felvärden eller text som inte kan översättas till tal ignoreras.
-
Om ett argument är en matris eller en referens räknas endast talen i matrisen eller referensen. Tomma celler, logiska värden, text eller felvärden i matrisen eller referensen ignoreras.
-
Kommentarer
-
Investeringen i NETNUVÄRDE börjar en period före datumet för betalningen i värde1 och slutar med den sista betalningen i listan. Beräkningen av NETNUVÄRDE baseras på framtida betalningar. Om den första betalningen inträffar i början av den första perioden måste det värdet adderas till resultatet av NETNUVÄRDE och inte tas med i värde-argumenten. Se följande exempel för mer information.
-
Om n är antal betalningar i värde-listan så är formeln för NETNUVÄRDE:
-
NETNUVÄRDE påminner om funktionen NUVÄRDE. Den viktigaste skillnaden mellan NUVÄRDE och NETNUVÄRDE är att NUVÄRDE tillåter betalningar att börja antingen i periodens slut eller i periodens början. Till skillnad från de varierande betalningarna i NETNUVÄRDE måste betalningarna i NUVÄRDE vara konstanta under hela investeringen. Mer information om annuiteter och finansiella funktioner finns under NUVÄRDE.
-
NETNUVÄRDE relaterar också till funktionen IR (internränta). IR är den ränta för vilken NETNUVÄRDE ger resultatet noll: NETNUVÄRDE(IR(...); ...)=0.
Exempel
Kopiera exempeldata i följande tabell och klistra in dem i cell A1 i ett nytt Excel-kalkylblad. När du vill att formlerna ska visa resultat markerar du dem, trycker på F2 och sedan på Retur. Om det behövs kan du justera kolumnbredderna så att alla data visas.
|
Data |
Beskrivning |
|
|---|---|---|
|
0,1 |
Årlig diskonteringsränta |
|
|
-10000 |
Initialkostnad för investering ett år från dagens datum |
|
|
3000 |
Retur från första året |
|
|
4200 |
Retur från andra året |
|
|
6800 |
Retur från tredje året |
|
|
Formel |
Beskrivning |
Resultat |
|
=NETNUVÄRDE(A2; A3; A4; A5; A6) |
Nettonuvärdet för investeringen |
1 188,44 kr |
Exempel 2
|
Data |
Beskrivning |
|
|---|---|---|
|
0,08 |
Årlig diskonteringsränta. Kan representera inflationsräntan eller räntesatsen för en konkurrerande investering. |
|
|
-40000 |
Initialkostnad för investering |
|
|
8000 |
Retur från första året |
|
|
9200 |
Retur från andra året |
|
|
10000 |
Retur från tredje året |
|
|
12000 |
Retur från fjärde året |
|
|
14500 |
Retur från femte året |
|
|
Formel |
Beskrivning |
Resultat |
|
=NETNUVÄRDE(A2; A4:A8)+A3 |
Nettonuvärdet för investeringen |
1 922,06 kr |
|
=NETNUVÄRDE(A2; A4:A8; -9000)+A3 |
Nettonuvärdet för investeringen med en förlust under det sjätte året på 9000 |
(3 749,47 kr) |