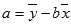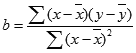SKÄRNINGSPUNKT (Funktionen SKÄRNINGSPUNKT)

Beskrivning

Beräknar punkten där en linje skär y-axeln genom att använda befintliga x-värden och y-värden. Skärningspunkten är baserad på en regressionslinje som dragits genom de kända x-värdena och de kända y-värdena. Använd funktionen SKÄRNINGSPUNKT när du vill avgöra värdet på den beroende variabeln när den oberoende variabeln är 0 (noll). Du kan också använda funktionen SKÄRNINGSPUNKT för att förutsäga det elektriska motståndet för en metall vid 0°C om datapunkterna registrerades i exempelvis rumstemperatur och högre temperatur.

Syntax

SKÄRNINGSPUNKT(kända_y; kända_x)

Syntaxen för funktionen SKÄRNINGSPUNKT har följande argument:

• Kända_y    Obligatoriskt. Detta är den underordnade uppsättningen observationer eller data.

• Kända_x    Obligatoriskt. Detta är den överordnade uppsättningen observationer eller data.

Kommentarer

• Argumenten måste vara antingen tal eller namn, matriser eller referenser som innehåller tal.

• Om ett matris- eller referensargument innehåller text, logiska värden eller tomma celler ignoreras dessa värden. Celler med värdet 0 tas däremot med i beräkningen.

• Om kända_x och kända_y innehåller olika antal datapunkter eller saknar datapunkter returnerar SKÄRNINGSPUNKT felvärdet #Saknas!.

• Ekvationen för regressionslinjens skärningspunkt är:

  

  där lutningen (b) är beräknad till:

  

  och där x och y är sampelmedelvärdena MEDEL(kända_x) och MEDEL(kända_y).

• Den underliggande algoritmen som används i funktionerna SKÄRNINGSPUNKT och LUTNING är inte samma som den underliggande algoritm som används i funktionen REGR. Skillnaden mellan dessa algoritmer kan leda till olika resultat vid obestämbara och parallella data. Exempel: om datapunkterna för argumentet kända_y är 0 och datapunkterna för argumentet kända_x är 1:

  • SKÄRNINGSPUNKT och LUTNING returnerar felet #DIVISION/0!. Algoritmen bakom SKÄRNINGSPUNKT och LUTNING har utformats att söka efter ett enda svar, och i det här exemplet kan det finnas mer än ett svar.

  • returnerar REGR värdet 0. Algoritmen bakom REGR har utformats att returnera rimliga resultat för parallella data, och i det här exemplet finns det minst ett svar.

Exempel

Kopiera exempeldata i följande tabell och klistra in dem i cell A1 i ett nytt Excel-kalkylblad. När du vill att formlerna ska visa resultat markerar du dem, trycker på F2 och sedan på Retur. Om det behövs kan du justera kolumnbredderna så att alla data visas.