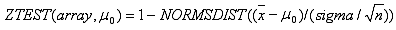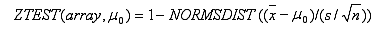บทความนี้จะอธิบายเกี่ยวกับไวยากรณ์ของสูตรและการใช้ฟังก์ชัน ZTEST ใน Microsoft Excel
ส่งกลับค่าความน่าจะเป็นด้านเดียวของ z-test ในค่าเฉลี่ยประชากรตามสมมติฐานนั้น μ0 ฟังก์ชัน ZTEST จะส่งกลับค่าความน่าจะเป็นที่ค่าเฉลี่ยของตัวอย่างจะสูงกว่าค่าเฉลี่ยของค่าที่สังเกตได้ในชุดข้อมูล (อาร์เรย์) นั่นคือค่าเฉลี่ยของตัวอย่างที่สังเกตได้
เมื่อต้องการดูวิธีการใช้ ZTEST ในสูตรเพื่อคำนวณค่า P แบบสองด้าน ให้ดูที่ "ข้อสังเกต" ด้านล่างนี้
สิ่งสำคัญ: ฟังก์ชันนี้ได้ถูกแทนที่ด้วยฟังก์ชันใหม่อย่างน้อยหนึ่งฟังก์ชันที่มีความถูกต้องแม่นยํายิ่งขึ้น และชื่อของฟังก์ชันสื่อถึงการใช้งานได้ดีขึ้น แม้ว่าฟังก์ชันนี้จะยังคงเข้ากันได้กับเวอร์ชันก่อนหน้า คุณควรพิจารณาใช้ฟังก์ชันใหม่จากนี้เนื่องจากฟังก์ชันนี้อาจไม่พร้อมใช้งานในเวอร์ชันExcelในอนาคต
สำหรับข้อมูลเพิ่มเติมเกี่ยวกับฟังก์ชันใหม่ ให้ดูที่ ฟังก์ชัน Z.TEST
ไวยากรณ์
ZTEST(array,x,[sigma])
ไวยากรณ์ของฟังก์ชัน ZTEST มีอาร์กิวเมนต์ดังนี้
-
อาร์เรย์ จำเป็น อาร์เรย์หรือช่วงข้อมูลที่จะทดสอบ x
-
X จำเป็น ค่าที่จะทดสอบ
-
Sigma ไม่จำเป็น ค่าเบี่ยงเบนมาตรฐาน (ที่ทราบค่า) ของประชากร ถ้าไม่ใส่ค่าไว้ จะใช้ค่าเบี่ยงเบนมาตรฐานของตัวอย่าง
ข้อสังเกต
-
ถ้า Array ว่างเปล่า ฟังก์ชัน ZTEST จะส่งกลับ #N/A เป็นค่าความผิดพลาด
-
ฟังก์ชัน ZTEST จะถูกคำนวณในรูปแบบต่อไปนี้ เมื่อมีการระบุค่า Sigma
หรือเมื่อไม่ได้ระบุค่า Sigma จะคำนวณดังนี้
โดยที่ X คือค่าเฉลี่ยเลขคณิตตัวอย่าง AVERAGE(array) และ s แทนค่าเบี่ยงเบนมาตรฐานตัวอย่าง STDEV(array) และ n คือจำนวนค่าที่สังเกตได้ในตัวอย่าง COUNT(array)
-
ZTEST คือความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างจะมากกว่าค่าสังเกต AVERAGE(array) เมื่อค่าเฉลี่ยประชากรที่เป็นตัวอย่างคือ μ0 จากสมมาตรของการแจกแจงปกติ ถ้า AVERAGE(array) < μ0 แล้ว ZTEST จะส่งกลับค่าที่มากกว่า 0.5
-
สูตร Excel ต่อไปนี้สามารถใช้ในการคำนวณค่าความน่าจะเป็นแบบสองด้าน ที่ค่าเฉลี่ยตัวอย่างจะแตกต่างจาก μ0 (ไม่ว่าในทิศทางใด) ไปมากกว่า AVERAGE(array) เมื่อค่าเฉลี่ยประชากรที่เป็นฐานคือ μ0
=2 * MIN(ZTEST(array,μ0,sigma), 1 - ZTEST(array,μ0,sigma))
ตัวอย่าง
คัดลอกข้อมูลตัวอย่างในตารางต่อไปนี้ และวางในเซลล์ A1 ของเวิร์กชีต Excel ใหม่ เพื่อให้สูตรแสดงผลลัพธ์ ให้เลือกสูตร กด F2 แล้วกด Enter ถ้าคุณต้องการ คุณสามารถปรับความกว้างของคอลัมน์เพื่อดูข้อมูลทั้งหมดได้
|
ข้อมูล |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
สูตร |
คำอธิบาย (ผลลัพธ์) |
ผลลัพธ์ |
|
=ZTEST(A2:A11,4) |
ค่าความน่าจะเป็นแบบด้านเดียวของ z-test ของชุดข้อมูลด้านบน โดยมีค่าเฉลี่ยประชากรที่ได้จากสมมติฐานเท่ากับ 4 (.090574) |
0.090574 |
|
=2 * MIN(ZTEST(A2:A11,4), 1 - ZTEST(A2:A11,4)) |
ค่าความน่าจะเป็นแบบสองด้านของ z-test ของชุดข้อมูลด้านบน โดยมีค่าเฉลี่ยประชากรที่ได้จากสมมติฐานเท่ากับ 4 (0.181148) |
0.181148 |
|
=ZTEST(A2:A11,6) |
ค่าความน่าจะเป็นแบบด้านเดียวของ z-test ของชุดข้อมูลด้านบน โดยมีค่าเฉลี่ยประชากรที่ได้จากสมมติฐานเท่ากับ 6 (0.863043) |
0.863043 |
|
=2 * MIN(ZTEST(A2:A11,6), 1 - ZTEST(A2:A11,6)) |
ค่าความน่าจะเป็นแบบสองด้านของ z-test ของชุดข้อมูลด้านบน โดยมีค่าเฉลี่ยประชากรที่ได้จากสมมติฐานเท่ากับ 6 (0.273913) |
0.273913 |
