LIJNSCH, functie

Beschrijving

Met de functie LIJNSCH berekent u de grootheden voor een lijn met de methode van de kleinste kwadraten om een rechte lijn te berekenen die het beste past bij uw gegevens, en wordt als resultaat een matrix gegeven die de lijn beschrijft. U kunt de functie LIJNSCH ook combineren met andere functies en zo de statistische gegevens voor andere typen modellen berekenen die lineaire modellen in de onbekende parameters zijn, waaronder machtreeksen en polynomiale, logaritmische en exponentiële reeksen. Omdat deze functie een matrix met waarden als resultaat geeft, moet de functie worden ingevoerd als een matrixformule. Instructies vindt u na de voorbeelden in dit artikel.

De vergelijking voor de lijn luidt als volgt:

y = mx + b

-of-

y = m1x1 + m2x2 + ... + b

als er meerdere bereiken van x-waarden zijn, waarbij de afhankelijke y-waarden een functie zijn van de onafhankelijke x-waarden. De m-waarden zijn coëfficiënten die corresponderen met de x-waarden en b is een constante. Let erop dat y, x en m vectoren kunnen zijn. Het resultaat van de functie LIJNSCH is {mn,mn-1,...,m1,b}. Met de functie LIJNSCH kunt u ook aanvullende regressiegrootheden berekenen.

Syntaxis

LIJNSCH(y-bekend;[x-bekend];[const];[stat])

De syntaxis van de functie LIJNSCH heeft de volgende argumenten:

Syntaxis

• y-bekend Vereist. De reeks y-waarden die u al kent uit de relatie y = mx + b.

  • Als het bereik van y-bekend één kolom is, wordt elke kolom van x-bekend als een afzonderlijke variabele beschouwd.

  • Als het bereik van y-bekend één rij is, wordt elke rij van x-bekend als een afzonderlijke variabele beschouwd.

• x-bekend Optioneel. Een optionele reeks x-waarden die u wellicht al kent uit de relatie y = mx + b.

  • Het bereik van x-bekend kan een of meer reeksen variabelen bevatten. Als slechts één variabele wordt gebruikt kunnen y-bekend en x-bekend bereiken met een willekeurige vorm zijn, mits deze dezelfde dimensie hebben. Als meerdere variabelen zijn gebruikt, moet y-bekend een vector zijn (dat wil zeggen een bereik van één rij hoog of één kolom breed).

  • Als u x-bekend weglaat, wordt uitgegaan van de matrix {1;2;3;...} met dezelfde afmetingen als y-bekend.

• const Optioneel. Een logische waarde die aangeeft of de constante b gelijkgesteld moet worden aan nul.

  • Als const WAAR is of wordt weggelaten, wordt b op de normale wijze berekend.

  • Als const ONWAAR is, krijgt b de waarde 0 en worden de m-waarden zodanig aangepast dat geldt y = mx.

• stat Optioneel. Een logische waarde die aangeeft of als resultaat ook aanvullende regressiegrootheden moeten worden gegeven.

  • Als statistieken WAAR zijn, retourneert LIJNENT de extra regressiestatistieken. als gevolg hiervan is de geretourneerde matrix {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r²,sey; F,df;ssreg,ssresid}.

  • Als stat ONWAAR is of wordt weggelaten, retourneert LIJNSCH alleen de m-coëfficiënten en de constante b.

    In de volgende tabel vindt u een overzicht van de aanvullende regressiegrootheden.

In de volgende afbeelding ziet u de volgorde waarin de aanvullende regressiegrootheden worden weergegeven.

Opmerkingen

• Elke rechte lijn kan worden beschreven aan de hand van een richtingscoëfficiënt en een snijpunt met de y-as.

  Richting (m):
  Als u de richting van een lijn wilt vinden, vaak geschreven als m, neemt u twee punten op de regel (x1,y1) en (x2,y2); de richting is gelijk aan (y2 - y1)/(x2 - x1).

  Y-intercept (b):
  De y-intercept van een lijn, vaak geschreven als b, is de waarde van y op het punt waar de lijn de y-as kruist.

  De vergelijking voor een rechte lijn is y = mx + b. Als u de waarden voor m en b kent, kunt u elk punt op die lijn berekenen door de x- of de y-waarde in te vullen. U kunt ook de functie TREND gebruiken.

• Als er slechts één onafhankelijke x-variabele is, kunt u de richtingscoëfficiënt en het snijpunt met de y-as met de volgende formules berekenen.

  Richting:
  =INDEX(LIJNLIJNEN(known_y,known_x's),1)

  Y-intercept:
  =INDEX(LIJNLIJNEN(known_y,known_x's),2)

• De nauwkeurigheid van de lijn die u hebt berekend met de functie LIJNSCH is afhankelijk van de mate van spreiding in de gebruikte gegevens. Hoe meer de grafische weergave van uw gegevens een rechte lijn benadert, des te nauwkeuriger is de vergelijking die door LIJNSCH wordt berekend. LIJNSCH maakt gebruik van de 'kleinste kwadraten'-methode voor het berekenen van de lijn die het beste past bij de gegevens. Als er slechts één onafhankelijke x-variabele is, kunt u m en b met de volgende formules berekenen:

  

  

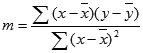
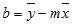
  waarbij x en y steekproefgemiddelden zijn, d.w.z. x = GEMIDDELDE(x-bekend) en y = GEMIDDELDE(y-bekend).

• De lijn- en curve-fittingsfuncties LINEST en LOGEST kunnen de beste rechte lijn of exponentiële curve berekenen die past bij uw gegevens. U moet echter bepalen welke van de twee resultaten het beste bij uw gegevens past. U kunt TREND(known_y's,known_x's) berekenen voor een rechte lijn of GROEI(known_y's, known_x's)voor een exponentiële curve. Deze functies, zonder het argument new_x van de groep, retourneren een matrix met y-waarden die langs die lijn of curve zijn voorspeld op uw werkelijke gegevenspunten. Vervolgens kunt u de voorspelde waarden vergelijken met de werkelijke waarden. Mogelijk wilt u ze beide in kaart brengen voor een visuele vergelijking.

• In regressieanalyse Excel voor elk punt het kwadraatsverschil tussen de y-waarde die voor dat punt wordt geschat en de werkelijke y-waarde. De som van deze kwadraatsverschillen wordt de resterende som van kwadraat genoemd, ssresid. Excel berekent vervolgens de totale som van kwadraat, sstotaal. Wanneer het argument const = WAAR of wordt weggelaten, is de totale som van kwadraat de som van de kwadraatsverschillen tussen de werkelijke y-waarden en het gemiddelde van de y-waarden. Wanneer het argument const = ONWAAR is, is de totale som van kwadraat de som van de kwadraat van de werkelijke y-waarden (zonder de gemiddelde y-waarde af te trekken van elke afzonderlijke y-waarde). Vervolgens kan regressie som van kwadraat, ssreg, worden gevonden van: ssreg = sstotal - ssresid. Hoe kleiner de resterende som van kwadraat is, vergeleken met de totale som van kwadraat, hoe groter de waarde van de bepalingscoëfficiënt, r^2,wat een indicator is voor hoe goed de vergelijking die het resultaat is van de regressieanalyse de relatie tussen de variabelen verklaart. De waarde van r² is gelijk aan ssreg/sstotal.

• In sommige gevallen hebben een of meer van de X-kolommen (ervan uit dat Y's en X's in kolommen staan) mogelijk geen extra voorspellende waarde in de aanwezigheid van de andere X-kolommen. Met andere woorden, het verwijderen van een of meer X-kolommen kan leiden tot voorspelde Y-waarden die even nauwkeurig zijn. In dat geval moeten deze redundante X-kolommen worden weggelaten uit het regressiemodel. Dit verschijnsel wordt 'collineariteit' genoemd, omdat elke redundante X-kolom kan worden uitgedrukt als een som van veelvouden van de niet-redundante X-kolommen. De functie LIJNENT controleert op collineariteit en verwijdert overtollige X-kolommen uit het regressiemodel wanneer deze worden geïdentificeerd. Verwijderde X-kolommen kunnen worden herkend in de LIJN.T-uitvoer als 0-coëfficiënten naast 0 se-waarden. Als een of meer kolommen als redundant worden verwijderd, wordt df beïnvloed omdat df afhankelijk is van het aantal X-kolommen dat daadwerkelijk voor voorspellende doeleinden wordt gebruikt. Zie Voorbeeld 4voor meer informatie over de berekening van df. Als df wordt gewijzigd omdat redundante X-kolommen worden verwijderd, worden ook de waarden sey en F beïnvloed. Collineariteit moet in de praktijk relatief zeldzaam zijn. De kans is echter groter dat sommige X-kolommen slechts 0- en 1-waarden bevatten als indicatoren voor het al dan niet lid zijn van een bepaald groep. Als const = WAAR wordt weggelaten of weggelaten, wordt met de functie LIJNENT effectief een extra X-kolom van alle 1 waarden invoegt om de onderschepping te modelleren. Als u een kolom met een 1 voor elk onderwerp hebt als dit niet het geval is, of 0 indien niet, en u hebt ook een kolom met een 1 voor elk onderwerp als vrouw of 0 als dat niet het geval is, is deze laatste kolom overbodig omdat de vermeldingen in deze kolom kunnen worden verkregen door de vermelding in de kolom 'mannelijke indicator' af te trekken van de vermelding in de extra kolom van alle 1 waarden die zijn toegevoegd door de functie LIJNENT.

• De waarde van vg wordt als volgt berekend wanneer geen X-kolommen uit het model worden verwijderd vanwege collineariteit: als er k kolommen zijn van x-bekend en const = WAAR of is weggelaten, dan vg = n – k – 1. Als const = ONWAAR, dan vg = n - k. In beide gevallen verhoogt elke kolom die vanwege collineariteit is verwijderd vg met 1.

• Bij het invoeren van een matrixconstante (bijvoorbeeld x-bekend) als argument gebruikt u puntkomma's om waarden in dezelfde rij van elkaar te scheiden en backslashes om rijen van elkaar te scheiden. Afhankelijk van uw landinstelling kunnen er andere scheidingstekens worden gebruikt.

• Houd er rekening mee dat y-waarden die met een regressievergelijking zijn voorspeld, onjuist kunnen zijn als deze buiten het bereik van de y-waarden vallen dat u hebt gebruikt bij het bepalen van de vergelijking.

• De onderliggende algoritme van de functies RICHTING en SNIJPUNT is anders dan die van de functie LIJNSCH. Het verschil tussen beide algoritmen kan tot verschillende resultaten leiden voor onbepaalde en collineaire gegevens. Wanneer het argument y-bekend bijvoorbeeld 0 gegevenspunten heeft en x-bekend 1 gegevenspunt, gebeurt het volgende:

  • LIJNSCH retourneert een waarde van 0. De algoritme van de functie LIJNSCH is ontworpen voor het retourneren van redelijke resultaten van collineaire gegevens, en in dit geval kan er ten minste één antwoord worden gevonden.

  • SLOPE and INTERCEPT return a #DIV/0! weergegeven. Het algoritme van de functies SLOPE en INTERCEPT is ontworpen om te zoeken naar slechts één antwoord, en in dit geval kan er meer dan één antwoord zijn.

• Behalve dat u met de functie LOGSCH statistische gegevens voor andere regressietypen kunt berekenen, kunt u met de functie LIJNSCH een bereik van andere regressietypen berekenen door functies van de x- en y-variabelen als x- en y-reeksen voor LIJNSCH in te voeren. De volgende formule

  =LIJNSCH(ywaarden, xwaarden^KOLOM($A:$C))

  werkt wanneer u met een enkele kolom van y-waarden en een enkele kolom van x-waarden de kubieke (polynomiale rangorde 3) benadering in de volgende vorm berekent:

  y = m1*x + m2*x^2 + m3*x^3 + b

  U kunt de formule wijzigen om andere typen regressie te berekenen, maar in sommige gevallen moeten de uitkomstwaarden en andere statistieken worden aangepast.

• De F-toetswaarde die het resultaat is van de functie LIJNSCH, verschilt van de F-toetswaarde die het resultaat is van de functie F.TOETS. LIJNSCH geeft de F-statistiek als resultaat, terwijl F.TOETS de kans als resultaat geeft.

Voorbeelden