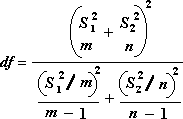Korzystając z pakietu Analysis ToolPak, można zaoszczędzić czas i zmniejszyć liczbę czynności wykonywanych podczas opracowywania złożonych analiz statystycznych lub inżynierskich. Użytkownik dostarcza dane i parametry analiz, a narzędzie używa odpowiednich statystycznych lub inżynierskich funkcji makr, aby obliczyć wyniki i wyświetlić je w tabeli wyników. Niektóre narzędzia generują wykresy w dodatkowych tabelach wyników.
Funkcji analizy danych można jednocześnie używać tylko w jednym arkuszu kalkulacyjnym. Podczas przeprowadzania analizy danych dla pogrupowanych arkuszy wyniki będą wyświetlone w pierwszym arkuszu, a w pozostałych arkuszach pojawią się puste, sformatowane tabele. Aby przeprowadzić analizę danych w pozostałych arkuszach, należy powtórzyć obliczenia za pomocą narzędzia analizy dla każdego arkusza.
Dodatek Analysis ToolPak zawiera narzędzia opisane w kolejnych sekcjach. Aby uzyskać do nich dostęp, należy kliknąć przycisk Analiza danych w grupie Analiza na karcie Dane. Jeśli polecenie Analiza danych jest niedostępne, należy załadować dodatek Analysis ToolPak.
-
Kliknij kartę Plik, kliknij pozycję Opcje, a następnie kliknij kategorię Dodatki.
-
W polu Zarządzanie wybierz pozycję Dodatki programu Excel, a następnie kliknij przycisk Przejdź.
Jeśli korzystasz z programu Excel dla komputerów Mac, w menu Plik przejdź do pozycji Narzędzia > Dodatki programu Excel.
-
W oknie Dodatki zaznacz pole wyboru Analysis ToolPak, a następnie kliknij przycisk OK.
-
Jeśli pozycja Analysis ToolPak nie jest wyświetlana w polu Dostępne dodatki, kliknij przycisk Przeglądaj, aby odnaleźć ten dodatek.
-
Jeśli zostanie wyświetlony monit informujący o tym, że na komputerze nie zainstalowano pakietu Analysis ToolPak, kliknij przycisk Tak, aby zainstalować ten pakiet.
-
Uwaga: Aby dodać funkcje języka Visual Basic for Application (VBA) dla dodatku Analysis ToolPak, można w podobny sposób załadować także dodatek Analysis ToolPak — VBA. W polu Dostępne dodatki zaznacz pole wyboru Analysis ToolPak — VBA.
Narzędzie analityczne Anova umożliwia przeprowadzanie różnego typu analiz wariancji. Wybór odpowiedniego narzędzia zależy od liczby czynników oraz od liczby próbek testowanych populacji.
Anova: pojedynczy czynnik
To narzędzie wykonuje prostą analizę wariancji danych dla dwóch lub większej liczby próbek. Analiza przedstawia hipotezę, że każda próbka jest pobierana z tego samego rozkładu prawdopodobieństwa bazowego na podstawie hipotezy, że bazowe rozkłady prawdopodobieństwa nie są takie same dla wszystkich próbek. Jeśli istnieją tylko dwie próbki, możesz użyć funkcji arkusza T.TEST. W przypadku więcej niż dwóch próbek nie ma wygodnej uogólnienia T.TEST, a zamiast tego można wywołać model Single Factor Anova.
Anova: dwa czynniki z replikacją
To narzędzie analityczne jest przydatne, gdy dane można klasyfikować w dwóch różnych wymiarach. Na przykład w ramach eksperymentu w celu zmierzenia wysokości roślin, rośliny mogą otrzymać różne marki nawozów (na przykład A, B, C) i mogą być przechowywane w różnych temperaturach (na przykład niskie, wysokie). Dla każdej z sześciu możliwych par {nawóz, temperatura}, mamy taką samą liczbę obserwacji wysokości roślin. Korzystając z tego narzędzia Anova, możemy przetestować:
-
Wysokości roślin dla nawozów różnych marek są pobierane z tej samej populacji źródłowej. Podczas tej analizy temperatury są ignorowane.
-
Wysokości roślin dla różnych poziomów temperatur są pobierane z tej samej populacji źródłowej. Podczas tej analizy są ignorowane marki nawozów.
Przy określaniu wpływu różnic między markami nawozów w punkcie 1 i różnic temperatur w punkcie 2 sześć próbek reprezentujących wszystkie pary wartości {nawóz, temperatura} pochodzi z tej samej populacji. Hipoteza alternatywna zakłada, że wpływ określonych par {nawóz, temperatura} jest większy niż różnice związane tylko z nawozem lub tylko z temperaturą.
Anova: dwa czynniki bez replikacji
To narzędzie analityczne jest przydatne, gdy dane są sklasyfikowane w dwóch różnych wymiarach, tak jak podczas analizy dwóch czynników z replikacją. Jednak w przypadku tego narzędzia zakłada się, że każda para jest obserwowana tylko raz (na przykład każda para {nawóz, temperatura} w poprzednim przykładzie).
Funkcje arkusza CORREL i PEARSON obliczają współczynnik korelacji między dwiema zmiennymi pomiarowymi, gdy dla każdej zmiennej są obserwowane pomiary dla każdej zmiennej N. (Brak obserwacji w przypadku jakichkolwiek przyczyn podmiotów, które podlegają zignorowaniu w analizie). Narzędzie do analizy korelacji jest szczególnie przydatne, gdy istnieje więcej niż dwie zmienne pomiarowe dla każdego z n podmiotów. Udostępnia tabelę wyjściową, macierz korelacji, która pokazuje wartość funkcji CORREL (lub PEARSON) zastosowaną do każdej możliwej pary zmiennych pomiarowych.
Współczynnik korelacji, podobnie jak kowariancja, jest miarą zakresu, w jakim dwie zmienne pomiarowe "różnią się razem". W przeciwieństwie do kowariancji współczynnik korelacji jest skalowany tak, aby jego wartość była niezależna od jednostek, w których wyrażone są dwie zmienne pomiarowe. (Jeśli na przykład dwie zmienne pomiarowe to waga i wzrost, wartość współczynnika korelacji pozostaje niezmieniona, jeśli waga jest konwertowana z kilogramów na kilogramy). Wartość współczynnika korelacji musi wynosić od -1 do +1 włącznie.
Narzędzie analityczne korelacji pozwala sprawdzić każdą parę zmiennych pomiarowych i stwierdzić, czy dwie zmienne pomiarowe mają tendencję do jednoczesnego zmieniania się — czy duże wartości jednej zmiennej raczej odpowiadają dużym wartościom drugiej zmiennej (korelacja dodatnia), czy małe wartości jednej zmiennej raczej odpowiadają dużym wartościom drugiej zmiennej (korelacja ujemna), czy też wartości obu zmiennych są od siebie niezależne (korelacja bliska zeru).
Narzędzia korelacji i kowariancji mogą być używane w tym samym ustawieniu, gdy na zbiorze jednostek występują inne zmienne pomiarowe N. Narzędzia korelacji i kowariancji dają tabelę wyjściową, macierz, która pokazuje współczynnik korelacji lub kowariancję odpowiednio między każdą parą zmiennych pomiarowych. Różnica polega na tym, że współczynniki korelacji są skalowane tak, aby mieściły się między -1 a +1 włącznie. Odpowiednie kowariancje nie są skalowane. Zarówno współczynnik korelacji, jak i kowariancja są miarami zakresu, w jakim dwie zmienne "różnią się razem".
Narzędzie kowariancji oblicza wartość funkcji KOWARIANCJA. P dla każdej pary zmiennych pomiarowych. (Bezpośrednie stosowanie KOWARIANCJI. P zamiast narzędzia kowariancji jest rozsądną alternatywą, gdy istnieją tylko dwie zmienne pomiarowe, czyli N=2). Wpis po przekątnej tabeli wyjściowej narzędzia Kowariancji w wierszu i, kolumnie i jest kowariancją zmiennej miary i-tej samej. Jest to tylko wariancja populacji dla tej zmiennej, obliczona przez funkcję ARKUSZ WARIANCJA.P.
Narzędzie kowariancji pozwala sprawdzić każdą parę zmiennych pomiarowych i stwierdzić, czy dwie zmienne pomiarowe mają tendencję do jednoczesnego zmieniania się — czy duże wartości jednej zmiennej raczej odpowiadają dużym wartościom drugiej zmiennej (kowariancja dodatnia), czy małe wartości jednej zmiennej raczej odpowiadają dużym wartościom drugiej zmiennej (kowariancja ujemna), czy też wartości obu zmiennych są od siebie niezależne (kowariancja bliska zeru).
Narzędzie analityczne Statystyki opisowe tworzy raport oparty na standardowych parametrach statystycznych dla danych z zakresu wejściowego, dostarczając informacji o głównej tendencji i zmienności danych.
Narzędzie analityczne Wygładzanie wykładnicze służy do przewidywania wartości na podstawie prognozy dla poprzedniego okresu, skorygowanej o błąd, jaki w niej wystąpił. Narzędzie korzysta ze stałej wygładzania a, której wielkość określa stopień reakcji prognoz na błędy istniejące w poprzedniej prognozie.
Uwaga: Rozsądne wartości stałej wygładzania wynoszą od 0,2 do 0,3. Te wartości wskazują, że bieżąca prognoza powinna być korygowana o 20 do 30 procent w przypadku błędu w prognozie poprzedniej. Większe stałe owocują szybszą odpowiedzią, ale mogą skutkować błędami w prognozie. Mniejsze stałe mogą skutkować większą zwłoką w prognozowaniu wartości.
Narzędzie analityczne Test F: dwie próbki dla wariancji wykonuje test F na dwóch próbkach, porównując wariancje dla dwóch populacji.
Narzędzia Test F można na przykład użyć w odniesieniu do próbek czasu w pojedynku pływackim dla każdej z dwóch drużyn. Dzięki temu narzędziu można uzyskać wynik testu hipotezy zerowej, która zakłada, że dwie próbki pochodzą z rozkładów o równych wariancjach przeciwko hipotezie alternatywnej, która zakłada, że wariancje nie są równe w rozkładach podstawowych.
Narzędzie oblicza wartość f statystyki F (lub współczynnika F). Wartość f zbliżona do 1 stanowi dowód na to, że wariancje rozkładu podstawowego są równe. Jeżeli w tabeli wyników f < 1, „P(F <= f) jednostronna” daje prawdopodobieństwo obserwowania wartości statystyki F mniejszej niż f, gdy wariancje rozkładu są równe i „Wartość krytyczna jednostronna F” jest wartością krytyczną mniejszą od 1 dla wybranego poziomu istotności Alfa. Jeżeli f > 1, „P(F <= f) jednostronna” daje prawdopodobieństwo obserwowania wartości statystyki F większej od f, gdy wariancje rozkładu są równe i „Wartość krytyczna jednostronna F” daje wartość krytyczną większą od 1 dla wartości Alfa.
Narzędzie analiza Fouriera służy do rozwiązywania problemów w układach liniowych oraz analizy danych okresowych i używa do transformacji danych metody szybkiej transformaty Fouriera (FFT, Fast Fourier Transform). To narzędzie obsługuje również transformacje odwrotne, w których odwrotność danych przetransformowanych zwraca dane oryginalne.
Narzędzie analityczne Histogram służy do obliczania indywidualnych i skumulowanych częstotliwości dla danych znajdujących się w zakresach komórek oraz dla przedziałów danych. Narzędzie generuje dane dotyczące liczby wystąpień danej wartości w zbiorze danych.
Można na przykład wyznaczyć rozkład uzyskanych ocen w grupie liczącej 20 studentów. Tabela histogramu zawiera granice przedziałów oraz liczbę ocen między najniższą a bieżącą granicą. Najczęściej występująca ocena jest nazywana wartością modalną danych.
Porada: W programie Excel 2016 można teraz tworzyć histogramy i wykresy Pareto.
Narzędzie analityczne Średnia ruchoma przewiduje wartości w okresie prognozy na podstawie średniej wartości zmiennej dla określonej liczby poprzednich okresów. Średnia ruchoma dostarcza informacje o trendach, które nie byłyby widoczne przy obliczeniu średniej prostej dla wszystkich danych historycznych. Narzędzie to jest przydatne w przewidywaniu wielkości sprzedaży, poziomu zapasów magazynowych lub innych trendów. Każda wartość prognozy wynika z następującej formuły:
gdzie:
-
N jest liczbą poprzednich okresów uwzględnionych w obliczaniu średniej ruchomej
-
A j jest wartością rzeczywistą w chwili j
-
F j jest wartością prognozowaną w chwili j
Narzędzie analityczne Generowanie liczb losowych wypełnia zakres niezależnymi liczbami losowymi uzyskanymi z jednego z kilku dostępnych rozkładów. Umożliwia ono opisywanie elementów populacji przy użyciu rozkładu prawdopodobieństwa. Można na przykład użyć rozkładu normalnego, aby opisać populację wzrostu poszczególnych osób lub rozkładu Bernoulli'ego dla dwóch możliwych wyników, aby opisać populację wyników rzutu monetą.
Narzędzie analityczne Pozycja i Percentyl tworzy tabelę zawierającą pozycję porządkową i procentową każdej wartości w zbiorze danych. Względną pozycję wartości w zbiorze danych można analizować. To narzędzie korzysta z funkcji arkusza POZYCJA. EQ iPROCENT POZ.PROC. INC. Jeśli chcesz uwzględnić wartości powiązane, użyj funkcji POZYCJA. Funkcja EQ , która traktuje wartości powiązane jako mające taką samą pozycję, lub używa funkcji POZYCJA.Funkcja AVG , która zwraca średnią pozycję dla wartości powiązanych.
Narzędzie analityczne Regresja wykonuje analizę regresji liniowej, dopasowując linię do zbioru wyników eksperymentalnych za pomocą metody „najmniejszych kwadratów”. Umożliwia ono analizowanie wpływu, jaki na jedną zmienną zależną wywierają zmienne niezależne. Można na przykład przeanalizować wpływ czynników, takich jak wiek, wzrost i waga, na wyniki lekkoatlety. Opierając się na zbiorze danych dotyczących osiąganych wyników, każdemu z trzech czynników można przypisać udział w wyniku osiągniętym przez sportowca, a następnie na tej podstawie przewidywać rezultaty innego atlety.
Narzędzie Regresja korzysta z funkcji arkusza REGLINP.
Narzędzie analityczne Próbkowanie tworzy próbkę z populacji, traktując populację jako zakres wejściowy. Jeśli populacja jest zbyt liczna, aby poddać ją przetwarzaniu lub przedstawić na wykresie, można posłużyć się próbką reprezentatywną. Można również utworzyć próbkę zawierającą tylko wartości z określonej części cyklu, jeśli istnieje prawdopodobieństwo, że dane wejściowe mają charakter okresowy. Jeśli na przykład zakres wejściowy zawiera wielkości sprzedaży kwartalnej, to próbkowanie z okresem równym cztery powoduje umieszczenie w zakresie wyjściowym wartości dla tego samego kwartału.
Narzędzia analityczne Test t wykonujące dwie próby sprawdzają równość średnich populacji dla każdej próbki. W trzech narzędziach przyjęto różne założenia: wariancje populacji są równe, wariancje populacji nie są równe i dwie próbki stanowią obserwacje tych samych obiektów przed eksperymentem i po nim.
W przypadku wszystkich trzech poniższych narzędzi wartość statystyki t, czyli wartość t, jest obliczana i wyświetlana jako „t Stat” w tabelach wyników. W zależności od danych, ta wartość (t) może być ujemna lub nieujemna. Przy założeniu, że średnie z rozkładu podstawowego są równe, jeżeli t < 0, to wartość „P(T <= t) jednostronna” daje prawdopodobieństwo, że obserwowana wartość statystyki t będzie bardziej ujemna od t. Jeżeli t >=0, to wartość „P(T <= t) jednostronna” daje prawdopodobieństwo, że obserwowana wartość statystyki t będzie bardziej dodatnia od t. „Wartość krytyczna jednostronna t” stanowi wartość odcięcia, a prawdopodobieństwo zaobserwowania wartości statystyki t większej lub równej „Wartości krytycznej jednostronnej t” wynosi Alfa.
Wartość „P(T <= t) dwustronna” daje prawdopodobieństwo, że obserwowana wartość statystyki t będzie większa w wartości bezwzględnej od t. „Wartość krytyczna dwustronna P” daje wartość odcięcia, przy której prawdopodobieństwo uzyskania wartości obserwowanej statystyki t większej w wartości bezwzględnej od „Wartości krytycznej dwustronnej P” wynosi Alfa.
Test t: sparowany, dwie próby dla średnich
Test sparowany można stosować, jeżeli istnieje naturalne sparowanie obserwacji w próbach, na przykład w przypadku dwukrotnego badania próbki z grupy — przed eksperymentem i po nim. To narzędzie analityczne i zawarta w nim formuła przeprowadza sparowany test t Studenta dla dwóch próbek, pozwalający stwierdzić, czy obserwacje dokonane przed eksperymentem i obserwacje dokonane po eksperymencie mogą pochodzić z rozkładów z równą średnią z populacji. W tej formie testu t nie zakłada się, że wariancje obu populacji są równe.
Uwaga: To narzędzie wyznacza między innymi wariancję sumaryczną, będącą zakumulowaną miarą rozkładu danych wokół średniej, obliczoną na podstawie następującej formuły:
Test t: dwie próby przy założeniu równych wariancji
To narzędzie analityczne przeprowadza test t Studenta dla dwóch prób. W tej odmianie testu t zakłada się, że oba zbiory danych pochodzą z rozkładów z takimi samymi wariancjami. Test jest nazywany testem t-homoscedastycznym. Test t umożliwia określenie, czy dwie próbki mogą pochodzić z rozkładów o równych średnich z populacji.
Test t: dwie próby przy założeniu nierównych wariancji
To narzędzie analityczne przeprowadza test t Studenta dla dwóch prób. Ta forma testu t zakłada, że dwa zestawy danych pochodzą z rozkładów o nierównych wariancjach. Jest on określany jako heteroscedastic t-Test. Podobnie jak w przypadku poprzednich przypadków równe wariancje, można użyć tego testu t do określenia, czy dwie próbki mogą pochodzić z rozkładów o równych środkach z populacji. Użyj tego testu, jeśli w dwóch próbkach występują odrębne przedmioty. Użyj testu Sparowane opisanego w poniższym przykładzie, jeśli istnieje jeden zestaw przedmiotów, a dwie próbki reprezentują pomiary dla każdego obiektu przed i po leczeniu.
Wartość statystyczna t jest wyznaczana na podstawie następującej formuły:
Poniższa formuła służy do obliczania stopni swobody( df). Ponieważ wynik obliczeń zwykle nie jest liczbą całkowitą, wartość df jest zaokrąglana do najbliższej liczby całkowitej, aby uzyskać wartość krytyczną z tabeli t. Funkcja arkusza programu Excel T.Funkcja TEST używa obliczonej wartości df bez zaokrąglania, ponieważ można obliczyć wartość dla T.TEST z noninteger df. Ze względu na te różne podejścia do określania stopni swobody, wyniki T.Funkcja TEST i to narzędzie testu t będą się różnić w przypadku odchyleń nierównych.
Test z: Narzędzie analityczne Dwie próbki dla środków wykonuje test dwóch próbek z dla środków o znanych wariancjach. To narzędzie służy do testowania hipotezy null, że nie ma różnicy między dwoma środkami populacji wobec jednostronnych lub dwustronnych hipotez alternatywnych. Jeśli wariancje nie są znane, funkcja arkusza Z.Zamiast tego należy użyć funkcji TEST.
Podczas korzystania z narzędzia Test z należy odpowiednio interpretować wyniki. Wartość „P(Z <= z) jednostronna” jest naprawdę wartością P(Z >= MODUŁ.LICZBY(z)), czyli prawdopodobieństwem, że wartość z jest dalsza od 0 w tym samym kierunku co obserwowana wartość z, gdy średnie z populacji nie różnią się od siebie. Wartość „P(Z <= z) dwustronna” jest naprawdę wartością P(Z >= MODUŁ.LICZBY(z) lub Z <= -MODUŁ.LICZBY(z)), czyli prawdopodobieństwem, że wartość z jest dalsza od 0 w innym kierunku niż obserwowana wartość z, gdy średnie z populacji nie różnią się od siebie. Wynik dwustronny jest tylko wynikiem jednostronnym pomnożonym przez 2. Narzędzia Test z można także używać w przypadku hipotezy zerowej, która zakłada, że istnieje określona wartość niezerowa dla różnicy między dwiema średnimi z populacji. Można na przykład użyć tego testu w celu zbadania różnic w działaniu dwóch modeli samochodów.
Potrzebujesz dodatkowej pomocy?
Zawsze możesz zadać pytanie ekspertowi w społeczności technicznej programu Excel lub uzyskać pomoc techniczną w Społecznościach.
Zobacz też
Tworzenie histogramu w programie Excel 2016
Tworzenie wykresu Pareto w Excel 2016
Ładowanie dodatku Analysis ToolPak w programie Excel
Funkcje INŻYNIERSKIE (informacje)
Omówienie formuł w programie Excel
Jak unikać niepoprawnych formuł
Znajdowanie i poprawianie błędów w formułach
Skróty klawiaturowe i klawisze funkcyjne w programie Excel