Returnerar oberoendetestet. CHI2TEST returnerar värdet från chi2-fördelningen (χ2) för statistiken och rätt frihetsgrader. Du kan använda χ2-tester för att avgöra om hypotetiska resultat kan verifieras genom ett experiment.
Viktigt!: Den här funktionen har ersatts med minst en ny funktion som erbjuder förbättrad precision och vars namn bättre speglar deras användning. Även om funktionen är bakåtkompatibel bör du överväga att använda de nya funktionerna hädanefter eftersom det inte är säkert att den här funktionen är tillgänglig i framtida versioner av Excel.
Mer information om funktionen finns i Funktionen CHI2.TEST.
Syntax
CHI2TEST(observerat_omr;förväntat_omr)
Syntaxen för funktionen CHI2TEST har följande argument:
-
Observerat_omr Obligatoriskt. Det dataområde som innehåller observationer att testas mot förväntade värden.
-
Förväntat_omr Obligatoriskt. Det dataområde som innehåller förhållandet mellan produkten av rad- och kolumnsummor och totalsumman.
Kommentarer
-
Om observerat_omr och förväntat_omr har olika antal datapunkter, returnerar CHI2TEST felvärdet #N/A.
-
χ2-testet beräknar först en χ2-statistik med följande formel:
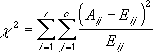
där:
Aij = observerad frekvens i i-raden, j-kolumnen
Eij = förväntad frekvens i i-raden, j-kolumnen
r = antalet rader
c = antalet kolumner
-
Ett lågt χ2-värde är ett tecken på oberoende. Som det framgår av formeln är χ2 alltid större än eller lika med 0, och endast 0 om Aij = Eij för alla i,j.
-
CHI2TEST returnerar sannolikheten att ett värde i χ2-statistiken som är minst lika högt som det värde som beräknas av formeln ovan kan ha inträffat av en slump under antagandet om oberoende. Vid beräkning av denna sannolikhet använder CHI2TEST χ2-fördelningen med lämpligt antal frihetsgrader, df. Om r > 1 och c > 1, så är fg = (r - 1)(c-1). Om r = 1 och c > 1, så är fg = c - 1 eller om r > 1 och c = 1, så är fg= r - 1. r = c = 1 är inte tillåtet och #SAKNAS! returneras.
-
Användningen av CHI2TEST fungerar bäst om Eij-värdena inte är för små. Vissa statistiker anser att Eij ska vara större än eller lika 5.
Exempel
Kopiera exempeldata i följande tabell och klistra in dem i cell A1 i ett nytt Excel-kalkylblad. När du vill att formlerna ska visa resultat markerar du dem, trycker på F2 och sedan på Retur. Om det behövs kan du justera kolumnbredderna så att alla data visas.
|
Män (Faktiskt) |
Kvinnor (Faktiskt) |
Beskrivning |
|
58 |
35 |
Instämmer |
|
11 |
25 |
Neutral |
|
10 |
23 |
Instämmer inte |
|
Män (Förväntat) |
Kvinnor (Förväntat) |
Beskrivning |
|
45,35 |
47,65 |
Instämmer |
|
17,56 |
18,44 |
Neutral |
|
16,09 |
16,91 |
Instämmer inte |
|
Formel |
Beskrivning |
Resultat |
|
=CHI2TEST(A2:B4;A6:B8) |
χ2-statistiken för ovanstående data är 16,16957 med 2 frihetsgrader. |
0,0003082 |










