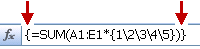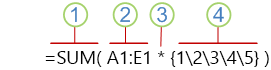Riktlinjer för och exempel på matrisformler

I den här övningen lär du dig att använda flercells- och encellsmatrisformler för att beräkna en uppsättning försäljningssiffror. I de första stegen används en flercellsformel för att räkna ut delsummor. I den andra delen används en encellsformel för att räkna ut en totalsumma.

• Flercellsmatrisformel

  

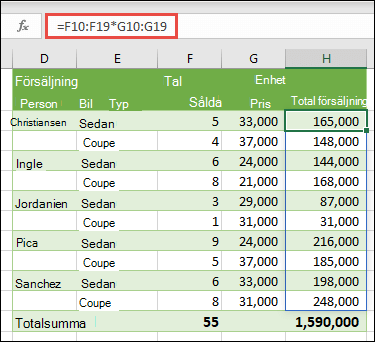
• Här beräknar vi den totala försäljningen av coupè och sedan för varje säljare genom att ange =F10:F19*G10:G19 i cell H10.

  När du trycker på Returså spills resultatet ned till cellerna H10:H19. Lägg märke till att spillområde är markerat med en kantlinje när du markerar en cell i spillområdet. Du kanske också märker att formlerna i cellerna H10:H19 är nedtonade. De finns bara där som referens, så om du vill justera formeln måste du markera cell H10, där huvudformeln finns.

• Encellsmatrisformel

  

  Skriv eller kopiera och klistra =SUMMA(F10:F19*G10:G19) i cell H20 i exempelarbetsboken och tryck sedan påRETUR.

  I det här fallet multipliceras värdena i matrisen (cellområdet F10 till G19) i Excel och sedan används funktionen SUMMA för att räkna ihop totalsumman. Resultatet blir en totalsumma på 1 590 000 $ i försäljning.

  I det här exemplet kan du se hur effektiv den här typen av formel kan vara. Tänk dig till exempel att du har 1 000 rader med data. Du kan summera delar av eller hela den här informationsmängden genom att skapa en matrisformel i en enda cell, i stället för att dra formeln ned över alla 1 000 raderna. Lägg också märke till att encellsformeln i cell h20 är helt fristående från flercellsformeln (formeln i cell H10 till H19). Det här är en annan fördel med att använda matrisformler – flexibilitet. Du kan ändra formlerna i kolumn H eller ta bort den kolumnen helt och hållet, utan att formeln i cell H20 påverkas. Det kan också vara bra att ha oberoende summor så här, eftersom det hjälper till att verifiera korrektheten i resultatet.

• Dynamiska matrisformler har dessutom följande fördelar:

  • Konsekvens    Om du klickar i några celler nedanför H10 kan du se att samma formel används. Med konsekvens blir resultatet också mer korrekt.

  • Säkerhet    Du kan inte skriva över en komponent i en flercellsmatrisformel. Klicka till exempel på cell H11 och tryck på Delete. Excel ändrar inte matrisens utdata. Om du vill ändra den måste du markera cellen längst upp till vänster i matrisen, eller cell H10.

  • Mindre filstorlekar    Ofta kan du använda en enda matrisformel i stället för flera delformler. Exemplet med bilförsäljningen använder till exempel en matrisformel för att beräkna resultaten i kolumn E. Om du använt standardformel som =F10*G10, F11*G11, F12*G12 osv. skulle du ha använt 11 olika formler för att beräkna samma resultat. Det är inget större problem, men tänk om du hade tusentals rader att summera? Det kan göra stor skillnad.

  • Effektivitet    Matrisfunktioner kan vara ett effektivt sätt att skapa komplexa formler. Matrisformeln =SUMMA(F10:F19*G10:G19) är densamma som den här: =SUMMA(F10*G10;F11*G11;F12*G12;F13*G13;F14*G14;F15*G15;F16*G16;F17*G17;F18*G18;F19*G19).

  • Spilla    Dynamiska matrisformel kommer automatiskt att spilla in i utdataområdet. Om dina understödjande data finns i en Excel-tabell ändras storleken på matrisen automatiskt när du lägger till eller tar bort data från matrisområdet om du använder strukturerade referenser.

  • #SPILL! Fel    Dynamiska matriser introducerade #SPILL! Fel, vilket anger att det avsedda spillområdet av någon anledning är blockerat. När du löser blockeringen spills formeln automatiskt.

Matriskonstanter är komponenter i matrisformler. Du skapar en matriskonstant genom att ange en lista över element och sedan manuellt omge listan med klammerparenteser ({ }), på det här sättet:

={1\2\3\4\5} eller ={"Januari"\"Februari"\"Mars"}

Om du avgränsar elementen med kommatecken skapar du en vågrät matris (en rad). Om du avgränsar elementen med semikolon skapar du en lodrät matris (en kolumn). Om du vill skapa en tvådimensionell matris avgränsar du elementen på varje rad med kommatecken och varje rad med semikolon.

I procedurerna nedan får du öva dig på att skapa vågräta, lodräta och tvådimensionella konstanter. Vi visar exempel med hjälp av funktionen SEKVENS för att automatiskt generera matriskonstanterna, samt manuellt angivna matriskonstanterna.

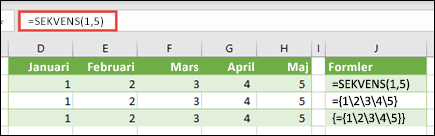
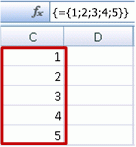
• Skapa en vågrät konstant

  Använd arbetsboken från tidigare exempel eller skapa en ny arbetsbok. Markera en tom cell och ange =SEKVENS(1,5). Funktionen SEKVENS skapar en matris på 1 rad och 5 KOLUMNER, samma som ={1\2\3\4\5}. Följande resultat visas:

  

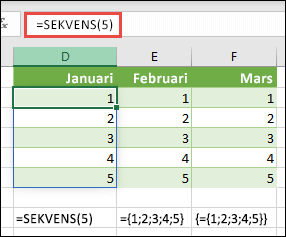
• Skapa en lodrät konstant

  Markera en tom cell med rum under och ange =SEKVENS(5)eller ={1;2;3;4;5}. Följande resultat visas:

  

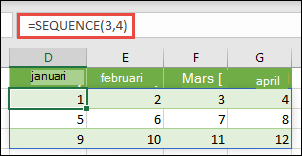
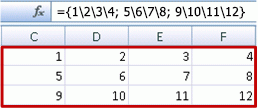
• Skapa en tvådimensionell konstant

  Markera en tom cell med rum till höger och under den och ange =SEKVENS(3,4). Följande resultat visas:

  

  Du kan också ange: eller ={1\2\3\4;5\6\7\8;9\10\11\12}, men var uppmärksam på var du lägger semikolon kontra kommatecken.

  Som du ser har alternativet SEKVENS betydande fördelar jämfört med att ange matriskonstantvärden manuellt. Det sparar främst tid, men det kan också minska fel vid manuell inmatning. Det är också lättare att läsa, särskilt eftersom semikolon kan vara svåra att skilja från kommaavgränsare.

Här är ett exempel som använder matriskonstanterna som en del av en större formel. I exempelarbetsboken går du till exempel konstant i en formel -kalkylblad, eller skapar ett nytt kalkylblad.

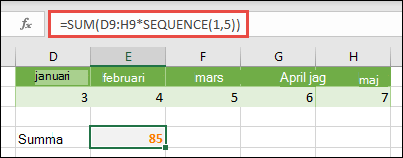
I cell D9 angav vi =SEKVENS(1,5,3,1), men du kan också ange 3, 4, 5, 6 och 7 i cellerna A9:H9. Det är inget särskilt med just det nummervalet. Vi valde bara något annat än 1–5 för att differentiera.

I cell E11 anger du =SUMMA(D9:H9*SEKVENS(1,5))eller =SUMMA(D9:H9*{1\2\3\4\5}). Formlerna returnerar 85.

Funktionen SEKVENS skapar motsvarigheten till matriskonstanten {1\2\3\4\5}. Eftersom åtgärder utförs på uttryck som omges av parenteser först blir de nästa två elementen som kommer in i ekvationen de cellvärden i (D9:H9) och operatorn (*). I det här läget multipliceras värdena i den sparade matrisen med de motsvarande värdena i konstanten. Det motsvarar:

=SUMMA(D9*1;E9*2;F9*3;G9*4;H9*5)eller =SUMMA(3*1;4*2;5*3;6*4;7*5)

Slutligen summeras värdena med funktionen SUMMA och returnerar 85.

För att undvika att använda den sparade matrisen och för att spara åtgärden helt och hållet i minnet kan du ersätta den sparade matrisen med en annan matriskonstant:

=SUMMA(SEKVENS(1;5;3;1)*SEKVENS(1;5))eller =SUMMA({3\4\5\6\7}*{1\2\3\4\5})

Element som du kan använda i matriskonstanter

• Matriskonstanterna kan innehålla tal, text, logiska värden (t.ex. SANT och FALSKT) och felvärden som #N/A. Du kan använda heltal, decimaltal och tal i exponentialform. Om du använder text måste du omge med dubbla citattecken ("text”).

• Matriskonstanter kan inte innehålla ytterligare matriser, formler eller funktioner. Med andra ord: de kan endast innehålla text eller tal som separeras av semikolon eller omvänt snedstreck. I Excel visas ett varningsmeddelande när du anger en formel, till exempel {1\2\A1:D4} eller {1\2\SUMMA(Q2:Z8)}. Numeriska värden kan inte innehålla procenttecken, dollartecken, punkter eller parenteser.

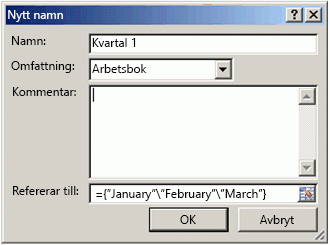
Ett av de bästa sätten att använda matriskonstanter är att namnge dem. Namngivna konstanter kan vara mycket enklare att använda och namnet kan dölja lite av komplexiteten med matrisformlerna för andra användare. Så här gör du när du vill namnge en matriskonstant och använda den i en formel:

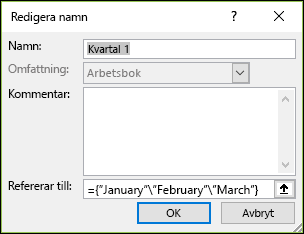
Gå till Formler > Definierade namn > Använd namn. I rutan Namn skriver du Kvartal1. Ange följande konstant i rutan Refererar till (kom ihåg att skriva in klammerparenteserna manuellt):

={”Januari”\”Februari”\”Mars”}

Dialogrutan bör nu se ut så här:

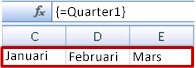
Klicka på OK, markera valfri rad med tre tomma celler och ange =Kvartal1.

Följande resultat visas:

Om du vill att resultatet ska spilla lodrätt i stället för vågrätt kan du använda =TRANSPONERA(Kvartal1).

Om du vill visa en lista med 12 månader, som du kanske använder när du skapar en ekonomiräkning, kan du basera en av dem på det aktuella året med funktionen SEKVENS. Det bästa med den här funktionen är att även om bara månaden visas finns det ett giltigt datum bakom sig som du kan använda i andra beräkningar. Du hittar de här exemplen på exempeldatauppsättningen Namngiven matriskonstant och Exempeldatauppsättningen i kalkylblad i exempelarbetsboken.

=TEXT(DATUM(ÅR(IDAG()),SEKVENS(1,12),1),"mmm")

Då används funktionen DATUM för att skapa ett datum baserat på det aktuella året, SEKVENS skapar en matriskonstant från 1 till 12 för januari till december och sedan konverterar funktionen TEXT visningsformatet till "mmm" (januari, februari, mars osv.). Om du vill visa det fullständiga månadsnamnet, till exempel januari, använder du "mmmm".

När du använder en namngiven konstant som en matrisformel ska du komma ihåg att ange likhetstecknet, som i =Kvartal1, inte bara Kvartal1. Om du inte gör det tolkas matrisen som en textsträng och formeln fungerar inte som avsett. Kom också ihåg att du kan använda kombinationer av funktioner, text och tal. Det beror på hur kreativ du vill vara.

I exemplen nedan visas några sätt som du kan använda matriskonstanter i matrisformler. I vissa exempel används funktionen TRANSPONERA för att konvertera rader till kolumner och tvärtom.

• Multiplicera alla element i en matris

  Ange =SEKVENS(1,12)*2eller ={1\2\3\4;5\6\7\8;9\10\11\12}*2

  Du kan också dividera med (/), addera med (+) och subtrahera med (-).

• Upphöja elementen i en matris i kvadrat

  Ange =SEKVENS(1,12)^2eller ={1\2\3\4;5\6\7\8;9\10\11\12}*2

• Hitta kvadratroten av kvadratobjekt i en matris

  Ange =SQRT(SEKVENS(1,12)^2)eller =SQRT({1\2\3\4;5\6\7\8;9\10\11\12}^2)

• Transponera en endimensionell rad

  Ange =TRANSPONERA(SEKVENS(1,5))eller =TRANSPONERA({1\2\3\4\5})

  Även om du angav en vågrät matriskonstant konverteras matriskonstanten till en kolumn med funktionen TRANSPONERA.

• Transponera en endimensionell kolumn

  Ange =TRANSPONERA(SEKVENS(5,1))eller =TRANSPONERA({1\2\3\4\5})

  Även om du angav en lodrät matriskonstant konverteras konstanten till en rad med funktionen TRANSPONERA.

• Transponera en tvådimensionell konstant

  Ange =TRANSPONERA(SEKVENS(3,4))eller =TRANSPONERA({1\2\3\4;5\6\7\8;9\10\11\12})

  Med funktionen TRANSPONERA konverteras varje rad till en serie kolumner.

Det här avsnittet innehåller exempel på grundläggande matrisformler.

• Skapa en matris från befintliga värden

  I följande exempel förklaras hur du använder matrisformel för att skapa en ny matris från en befintlig matris.

  Ange =SEKVENSER(3,6,10,10), eller ={10\20\30\40\50\60;70\80\90\100\110\120;130\140\150\160\170\180}

  Glöm inte att ange { (vänster klammerparentes) innan du anger 10 och } (höger klammerparentes) efter att du anger 180 eftersom du skapar en matris med tal.

  Ange sedan =D9#eller =D9:I11 i en tom cell. En 3 x 6 cellmatris visas med samma värden som i D9:D11. #-tecknet kallas för spilltområdesoperator, och det är Excels sätt att referera till hela matrisområdet i stället för att behöva skriva det.

  

• Skapa en matriskonstant från befintliga värden

  Du kan ta resultatet av en spilld matrisformel och konvertera den till dess komponentdelar. Markera cell D9 och tryck sedan på F2 om du vill växla till redigeringsläge. Tryck sedan på F9 om du vill konvertera cellreferenser till värden, som Excel sedan konverterar till en matriskonstant. När du trycker på RETRU, ska formeln = D9# nu vara ={10\20\30;40\50\60;70\80\90}.

• Räkna tecken i ett cellområde

  I följande exempel visas hur du räknar antalet tecken i ett cellområde. Det omfattar blanksteg.

  

  =SUMMA(LÄNGD(C9:C13))

  I det här fallet returnerar funktionen LÄNGD längden på varje textsträng i var och en av cellerna i området. Sedan adderas dessa värden med funktionen SUMMA och resultatet (66) visas. Om du vill ha genomsnittligt antal tecken kan du använda:

  =MEDEL(LÄNGD(C9:C13))

• Innehållet i den längsta cellen i cellområdet C9:C13

  =INDEX(C9:C13,MATCH(MAX(LEN(C9:C13)),LEN(C9:C13),0),1)

  Formeln fungerar endast när ett dataområde innehåller en enda cellkolumn.

  Vi tittar närmare på formeln, med början från inre element och arbetar utåt. Funktionen LÄNGD returnerar längden på varje post i cellområdet D2:D6. Funktionen MAX beräknar det största värdet bland dessa element, som motsvarar den längsta textsträngen, som finns i cell D3.

  Det är nu det börjar bli komplicerat. Med funktionen PASSA beräknas adressen (den relativa positionen) för den cell som innehåller den längsta textsträngen. För detta behövs tre argument: ett sökvärde, en sökmatris och en passningstyp. Funktionen PASSA söker efter sökvärdet i sökmatrisen. I det här fallet är sökvärdet den längsta textsträngen:

  MAX(LÄNGD(C9:C13)

  och den strängen finns i den här matrisen:

  LÄNGD(C9:C13)

  Matchningsargumentet i det här fallet är 0. Passningstypen kan vara värdet 1, 0 eller -1.

  • 1 - returnerar det högsta värdet som är lägre än eller lika med sökvärdet

  • 0 - returnerar det första värdet som är exakt lika med sökvärdet.

  • 1 - returnerar det lägsta värdet som är högre än eller lika med det angivna sökvärdet.

  • Om du utelämnar passningstypen används 1 som standard.

  Slutligen används de här argumenten av funktionen INDEX: en matris samt ett värde som anger rad och kolumn inom den matrisen. Cellområdet C9:C13 står för matrisen, funktionen PASSA står för celladressen och det sista argumentet (1) anger att värdet kommer från den första kolumnen i matrisen.

  Om du vill få fram innehållet i den minsta textsträngen ersätter du MAX i exemplet ovan med MIN.

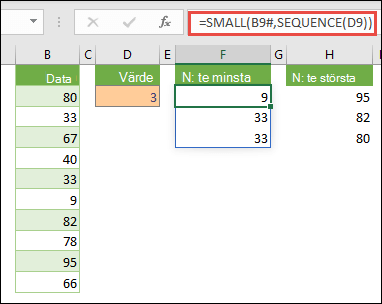
• Hitta de n lägsta värdena i ett område

  Det här exemplet visar hur du hittar de tre minsta värdena i ett cellområde, där en matris med exempeldata i cellerna B9:B18 har skapats med: =HELTA(SLUMPARRAY(10;1)*100). Observera att SLUMPMATRIS är en beräkningsbarfunktion, så du får en ny uppsättning slumptal varje gång Excel beräknar.

  

  Ange =LITEN(B9#;SEKVENS(D9), =LITEN(B9:B18,{1\2\3})

  Den här formeln använder en matriskonstant för att utvärdera funktionen MINSTA tre gånger och returnera de minsta 3 medlemmarna i matrisen som finns i cellerna B9:B18, där 3 är ett variabelvärde i cell D9. Om du vill hitta fler värden kan du öka värdet i funktionen SEKVENS eller lägga till fler argument till konstanten. Du kan också använda ytterligare funktioner med den här formeln, till exempel SUMMA eller MEDEL. Till exempel:

  =SUMMA(LITEN(B9#;SEKVENS(D9))

  =MEDEL(LITEN(B9#;SEKVENS(D9))

• Hitta de n högsta värdena i ett område

  Om du vill hitta de högsta värdena i ett område kan du ersätta funktionen MINSTA med funktionen STÖRSTA. Dessutom används funktionerna RAD och INDIREKT i exemplet nedan.

  Ange =STOR(B9#;RAD(INDIREKT("1:3")))eller =STOR(B9:B18;RAD(INDIREKT("1:3")))

  I det här läget kan det vara bra att känna till lite grann om funktionerna RAD och INDIREKT. Du kan använda funktionen RAD när du vill skapa en matris med upprepade heltal. Välj t.ex. en tom och ange:

  =RAD(1:10)

  Formeln skapar en kolumn med tio heltal i följd. Om du vill se ett potentiellt problem infogar du en rad ovanför området som innehåller matrisformeln (d.v.s. ovanför rad 1). Radreferenserna justeras i Excel och formeln genererar nu heltal från 2 till 11. Du kan åtgärda problemet genom att lägga till funktionen INDIREKT i formeln:

  =RAD(INDIREKT("1:10"))

  I funktionen INDIREKT används textsträngar som argument (vilket är anledningen till att området 1:10 omges av citattecken). Textvärden justeras inte när du infogar rader eller flyttar matrisformeln på något annat sätt. Resultatet blir att funktionen RAD alltid genererar den matris med heltal som du vill ha. Det är lika enkelt att använda SEKVENS:

  =SEKVENS(10)

  Vi tar en titt på formeln som du använde tidigare –=STÖRSTA(B9#;RAD(INDIREKT("1:3"))) – med början från den inre parentesen och arbetar utåt: Funktionen INDIREKT returnerar en uppsättning textvärden, i det här fallet värdena 1 till 3. Funktionen RAD genererar i sin tur en kolumnmatris med tre celler. Funktionen STOR använder värdena i cellområdet B9:B18 och utvärderas tre gånger, en gång för varje referens som returneras av funktionen RAD. Om du vill hitta fler värden lägger du till ett större cellområde i funktionen INDIREKT. Slutligen kan du, som med exemplen på SMÅ, använda den här formeln med andra funktioner, till exempel SUMMA och MEDEL.

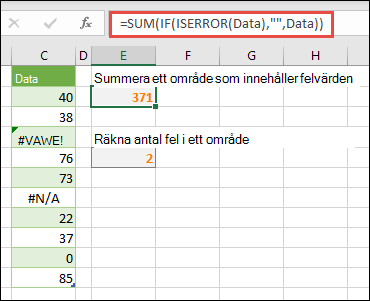
• Summera ett område som innehåller felvärden

  Funktionen SUMMA i Excel fungerar inte när du försöker summera ett område som innehåller ett felvärde, till exempel #VÄRDE! eller #EJ TILLÄMPLIG. I det här exemplet får du veta hur du summerar värdena i ett område med namnet Data som innehåller fel:

  

• =SUMMA(OM(ÄRFEL(Data),"",Data))

  Formeln skapar en ny matris som innehåller de ursprungliga värdena minus eventuella felvärden. Om vi börjar från de innersta funktionerna och jobbar oss utåt söker funktionen ÄRFEL efter fel i cellområdet (Data). Funktionen OM returnerar ett visst värde om ett villkor som du anger valideras som SANT och ett annat värde om det valideras till FALSKT. I det här fallet returneras tomma strängar ("") för alla felvärden eftersom de valideras till SANT, och de återstående värdena från området (Data) returneras, eftersom de valideras till FALSKT, vilket innebär att de inte innehåller felvärden. Funktionen SUMMA räknar sedan ut totalsumman för den filtrerade matrisen.

• Räkna antalet felvärden i ett område

  Det här exemplet påminner om formeln ovan, men den returnerar antalet felvärden i ett område med namnet Data i stället för att filtrera ut dem:

  =SUMMA(OM(ÄRFEL(Data),1,0))

  Den här formeln skapar en matris som innehåller värdet 1 för de celler som innehåller fel och värdet 0 för celler som inte innehåller fel. Du kan förenkla formeln och få samma resultat genom att ta bort det tredje argumentet till funktionen OM, på det här sättet:

  =SUMMA(OM(ÄRFEL(Data),1))

  Om du inte anger argumentet returnerar funktionen IF värdet FALSKT om en cell inte innehåller ett felaktigt värde. Du kan förenkla formeln ännu mer:

  =SUMMA(OM(ÄRFEL(Data)*1))

  Den här varianten fungerar eftersom SANT*1=1 och FALSKT*1=0.

I vissa situationer kan du behöva summera värden baserat på villkor.

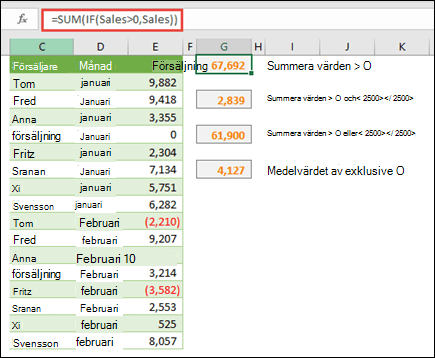
Den här matrisformeln summerar exempelvis bara de positiva heltalen i ett område som heter Försäljning, som representerar cellerna E9:E24 i exemplet ovan:

=SUMMA(OM(Försäljning>0,Försäljning))

Funktionen OM skapar en matris med positiva och falska värden. Funktionen SUMMA ignorerar praktiskt taget de falska värdena eftersom 0+0=0. Cellområdet som du använder i den här formeln kan bestå av vilket antal rader och kolumner som helst.

Du kan också summera värden som uppfyller fler än ett villkor. Den här matrisformeln beräknar till exempel värden som är större än 0 OCH mindre än 2500:

=SUMMA((försäljning>0)*(försäljning<2500)*(försäljning))

Kom ihåg att den här formeln returnerar ett fel om området innehåller en eller flera celler som inte innehåller tal.

Du kan också skapa matrisformler som använder ett slags ELLER-villkor. Du kan till exempel summera värden som är större än 0 ELLER som är mindre än 2500:

=SUMMA(OM((Försäljning>0)+(Försäljning<2500),Försäljning))

Det går inte att använda funktionerna OCHoch ELLER direkt i matrisformler eftersom dessa funktioner returnerar ett enda resultat, antingen SANT eller FALSKT, och matrisfunktionerna kräver resultatmatriser. Du kan lösa problemet genom att använda den logik som visas i den föregående formeln. Med andra ord: du utför matematiska operationer, till exempel addition eller multiplikation, på värden som uppfyller villkoret ELLER eller OCH.

I det här exemplet beskrivs hur du tar bort nollvärden från ett område när du behöver räkna ut ett genomsnitt för värdena i det området. I formeln används ett dataområde med namnet Försäljning:

=MEDEL(OM(Försäljning<>0,Försäljning))

Funktionen OM skapa en matris med värden som inte är lika med 0 och lämnar sedan dessa värden vidare till funktionen MEDEL.

I den här matrisformeln jämförs värdena i två cellområden med namnen Minadata och Dinadata och antalet skillnader mellan de två returneras. Om innehållet i de två områdena är identiskt returnerar formeln 0. Om du vill använda den här formeln måste cellområdena ha samma storlek och dimension. Till exempel om MyData är ett område med 3 rader och 5 kolumner måste YourData också bestå av 3 rader och 5 kolumner:

=SUMMA(OM(Minadata=Dinadata,0,1))

Formeln skapar en ny matris i samma storlek som de områden som du jämför. Funktionen OM fyller i matrisen med värdet 0 och värdet 1 (0 för felaktiga matchningar och 1 för identiska celler). Funktionen SUMMA returnerar summan av värdena i matrisen.

Du kan förenkla formeln så här:

=SUMMA(1*(Minadata<>Dinadata))

Precis som formeln som räknar felvärden i ett område, fungerar den här formeln eftersom SANT*1=1 och FALSKT*1=0.

Den här matrisformeln returnerar radnumret för det högsta värdet i ett enkolumnsområde med namnet Data:

=MIN(OM(Data=MAX(Data);RAD(Data);""))

Funktionen OM skapar en ny matris som motsvarar området Data. Om en motsvarande cell innehåller det högsta värdet i området innehåller matrisen radnumret. I annat fall innehåller matrisen en tom sträng (""). Funktionen MIN använder den nya matrisen som sitt andra argument och returnerar det lägsta värdet, som motsvarar radnumret för det högsta värdet i området Data. Om området Data innehåller identiska högsta värden returnerar formeln raden för det första värdet.

Om du vill returnera den faktiska celladressen för ett maxvärde kan du använda den här formeln:

=ADRESS(MIN(OM(Data=MAX(Data);RAD(Data);""));KOLUMN(Data))

I exempelarbetsboken finns liknande exempel på Skillnader mellan datauppsättningar-kalkylbladet.

I den här övningen lär du dig att använda flercells- och encellsmatrisformler för att beräkna en uppsättning försäljningssiffror. I de första stegen används en flercellsformel för att räkna ut delsummor. I den andra delen används en encellsformel för att räkna ut en totalsumma.

• Flercellsmatrisformel

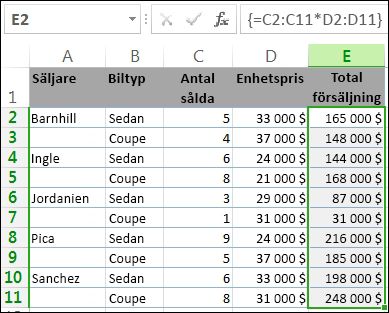
Kopiera hela tabellen nedan och klistra in den i cell A1 i ett tomt kalkylblad.

Säljare	Biltyp	Antal sålda  exemplar	Enhetspris	Total försäljning
Barnhill	Sedan	5	33000
	Kupé	4	37000
Ingle	Sedan	6	24000
	Kupé	8	21000
Jordan	Sedan	3	29000
	Kupé	1	31000
Pica	Sedan	9	24000
	Kupé	5	37000
Sanchez	Sedan	6	33000
	Kupé	8	31000
Formel (slutsumma)			Slutsumma
'=SUMMA(C2:C11*D2:D11)			=SUMMA(C2:C11*D2:D11)

1. Om du vill se den totala försäljningen av kupé och sedaner för varje säljare markerar du cellerna E2:E11, anger formeln =C2:C11*D2:D11och trycker sedan på Ctrl+Skift+Retur.

2. Om du vill visa Totalsumma för alla sålda objekt markerar du cell F11, anger formeln =SUMMA(C2:C11*D2:D11) och trycker på Ctrl+Skift+Retur.

När du trycker på Ctrl+Skift+Returomges formeln av klammerparenteser ({ }) och en instans av formeln infogas i varje cell i det markerade området. Det går väldigt snabbt, så det du ser i kolumn E är den totala försäljningssumman för varje biltyp per försäljare. Om du markerar E2 och sedan E3, E4 och så vidare ser du att samma formel visas: {=C2:C11*D2:D11}. 

• Skapa en encellsmatrisformel

Skriv in följande formel i cell D13, och tryck sedan på Ctrl+Skift+Retur:

=SUMMA(C2:C11*D2:D11)

I det här fallet multipliceras värdena i matrisen (cellområdet C2 till D11) i Excel och sedan används funktionen SUMMA för att räkna ihop totalsumman. Resultatet blir en totalsumma på 1 590 000 $ i försäljning. I det här exemplet kan du se hur effektiv den här typen av formel kan vara. Tänk dig till exempel att du har 1 000 rader med data. Du kan summera delar av eller hela den här informationsmängden genom att skapa en matrisformel i en enda cell, i stället för att dra formeln ned över alla 1 000 raderna.

Lägg också märke till att encellsformeln (i cell B13) är helt fristående från flercellsformeln (formeln i cell E2 till E11). Det här är en annan fördel med att använda matrisformler – flexibilitet. Du kan ändra formlerna i kolumn E eller ta bort den kolumnen helt och hållet, utan att formeln i cell D13 påverkas.

Matrisformler har dessutom följande fördelar:

• Konsekvens    Om du klickar i några celler nedanför E2 kan du se att samma formel används. Med konsekvens blir resultatet också mer korrekt.

• Säkerhet    Du kan inte skriva över en komponent i en flercellsmatrisformel. Klicka till exempel på cell E3 och tryck på Delete. Du måste antingen markera hela cellområdet (E2 till E11) och ändra formeln för hela matrisen, eller låta matrisen vara som den här. Som en extra säkerhetsåtgärd måste du trycka på Ctrl + Skift + Retur om du vill bekräfta en ändring i formeln.

• Mindre filstorlekar    Ofta kan du använda en enda matrisformel i stället för flera delformler. I arbetsboken används till exempel en matrisformel för att beräkna resultatet i kolumnen E. Om du hade använt standardformler (till exempel =C2*D2, C3*D3, C4*D4) hade du behövt använda 11 olika formler för att räkna ut samma resultat.

I allmänhet används vanlig formelsyntax i matrisformler. De börjar alltid med ett likhetstecken (=) och du kan använda de flesta av de inbyggda Excel-funktionerna i matrisformler. Den stora skillnaden när du använder en matrisformel är att du måste trycka på Ctrl+Skift+Retur när du vill ange formeln. När du gör det omges matrisformeln med klammerparenteser – om du skriver in klammerparenteserna manuellt konverteras formeln till en textsträng och fungerar inte.

Matrisfunktioner kan vara ett effektivt sätt att skapa komplexa formler. Matrisformeln =SUMMA(C2:C11*D2:D11) har samma resultat som det här: =SUMMA(C2*D2;C3*D3;C4*D4;C5*D5;C6*D6;C7*D7;C8*D8;C9*D9;C10*D10;C11*D11).

När du arbetar med flercellsformler ska du dessutom tänka på det här:

• Markera cellområdet där resultatet ska visas innan du anger formeln. Detta gjorde du när du skapade flercellsmatrisformeln när du markerade cell E2 till E11.

• Du kan inte ändra innehållet i en enskild cell i en matrisformel. Prova själv genom att markera cell E3 i kalkylbladet och trycka på Delete. Ett felmeddelande om att du inte kan ändra en del av matrisen visas.

• Du kan flytta eller ta bort en hel matrisformel, men det går inte att flytta eller ta bort delar av den. Med andra ord: om du vill minska ned en matrisformel tar du först bort formeln och börjar sedan om från början.

• Om du vill ta bort en matrisformel markerar du hela formelområdet (till exempel E2:E11), och trycker sedan på Delete.

• Det går inte att infoga tomma celler i eller ta bort celler från en flercellsmatrisformel.

Ibland kan du behöva utöka en matrisformel. Markera den första cellen i det befintliga matrisområdet och fortsätt tills du har markerat hela området som du vill utöka formeln till. Tryck på F2 för att redigera formeln och tryck sedan på CTRL + SKIFT + RETUR för att bekräfta formeln när du har justerat formelområdet. Nyckeln är att markera hela området, med början i den översta vänstra cellen i matrisen. Cellen längst upp till vänster är den som redigeras.

Matrisformler är mycket effektiva, men det finns några nackdelar:

• Ibland glömmer du att trycka på Ctrl + Skift + Retur. Det kan hända även till de mest erfarna Excel-användarna. Kom ihåg att trycka på den här tangentkombinationen när du anger eller redigerar en matrisformel.

• Andra som använder din arbetsbok kanske inte förstår hur formlerna fungerar. I praktiken är det sällan som det finns någon dokumentation om matrisformler i ett kalkylblad. så om andra personer behöver redigera dina arbetsböcker bör du antingen låta bli att använda matrisformler eller se till att andra användare känner till matrisformler och vet hur de ska ändra dem, om det skulle behövas.

• Beroende på datorns kapacitet kan stora matrisformler göra att beräkningar går långsammare.

Matriskonstanter är komponenter i matrisformler. Du skapar en matriskonstant genom att ange en lista över element och sedan manuellt omge listan med klammerparenteser ({ }), på det här sättet:

={1\2\3\4\5}

Vid det här laget vet du antagligen att du måste trycka på Ctrl+Skift+Retur när du skapar matrisformler. Eftersom matriskonstanter är komponenter i matrisformler omger du konstanterna med klammerparenteser manuellt genom att skriva in dem. Sedan trycker du på Ctrl+Skift+Retur när du vill ange hela formeln.

Om du avgränsar elementen med kommatecken skapar du en vågrät matris (en rad). Om du avgränsar elementen med semikolon skapar du en lodrät matris (en kolumn). Om du vill skapa en tvådimensionell matris avgränsar du elementen på varje rad med kommatecken och varje rad med semikolon.

Här är ett exempel på en rad: {1\2\3\4}. Här är exempel på en kolumn: {1;2;3;4}. Och här är ett exempel på två rader och fyra kolumner: {1\2\3\4;5\6\7\8}. I matrisen med två rader innehåller den första raden elementen 1, 2, 3 och 5, 6, 7, och den andra raden innehåller 8 och 4. Ett omvänt snedstreck används för att avgränsa de båda raderna, mellan elementet 4 och elementet 5.

Precis som med matrisformler kan du använda matriskonstanter med de flesta av de inbyggda funktionerna i Excel. I avsnitten nedan får du en förklaring på hur du skapar de olika typerna av konstanter och hur du använder konstanterna med funktioner i Excel.

I procedurerna nedan får du öva dig på att skapa vågräta, lodräta och tvådimensionella konstanter.

Skapa en vågrät konstant

1. Markera cell A1 till E1 i ett tomt kalkylblad.

2. Ange följande formel i formelfältet och tryck sedan på Ctrl+Skift+Retur:

   ={1\2\3\4\5}

   I det här fallet ska du skriva inledande och avslutande klammerparenteser ({ }), så lägger Excel till den andra uppsättningen åt dig.

   Följande resultat visas.

   

Skapa en lodrät konstant

1. Markera en kolumn med fem celler i kalkylbladet.

2. Ange följande formel i formelfältet och tryck sedan på Ctrl+Skift+Retur:

   ={1;2;3;4;5}

   Följande resultat visas.

   

Skapa en tvådimensionell konstant

1. Markera ett cellblock som är fyra kolumner brett och tre rader högt.

2. Ange följande formel i formelfältet och tryck sedan på Ctrl+Skift+Retur:

   ={1\2\3\4;5\6\7\8;9\10\11\12}

   Följande resultat visas.

   

Använda konstanter i formler

Här är ett enkelt exempel som använder konstanter:

1. Skapa ett nytt kalkylblad i exempelarbetsboken.

2. Skriv 3 i cell A1 och sedan 4 i B1, 5 i C1, 6 i D1 och 7 i E1.

3. Skriv in följande formel i cell A3, och tryck sedan på Ctrl+Skift+Retur:

   =SUMMA(A1:E1*{1\2\3\4\5})

   Lägg märke till att konstanten omges med ytterligare två klammerparenteser, eftersom du angav den som en matrisformel.

   

   Värdet 85 visas i cell A3.

I nästa avsnitt kan du se hur formeln fungerar.

Formeln som du precis använde innehåller flera delar.

1. Funktion

2. Sparad matris

3. Operator

4. Matriskonstant

Det sista elementet innanför parentesen är matriskonstanten: {1\2\3\4\5}. Kom ihåg att matriskonstanter inte omges med klammerparenteser av Excel: det måste du göra själv. Kom också ihåg att när du har lagt till en konstant i en matrisformel ska du trycka på Ctrl+Skift+Returr när du anger formeln.

Eftersom åtgärder utförs på uttryck som omges av parenteser först blir de nästa två elementen som kommer in i ekvationen de värden som sparas i kalkylbladet (A1:E1) och operatorn. I det här läget multipliceras värdena i den sparade matrisen med de motsvarande värdena i konstanten. Det motsvarar:

=SUMMA(A1*1;B1*2;C1*3;D1*4;E1*5)

Slutligen summeras värdena med funktionen SUMMA och summan 85 visas i cell A3:

För att undvika att använda den sparade matrisen och för att bara spara åtgärden helt och hållet i minnet ersätter du den sparade matrisen med en annan matriskonstant:

=SUMMA({3\4\5\6\7}*{1\2\3\4\5})

Prova detta genom att kopiera funktionen, markera en tom cell i kalkylbladet, klistra in formeln i formelfältet och tryck sedan på Ctrl+Skift+Returr. Du kan se samma resultat som du gjorde i den tidigare övningen med matrisformeln:

=SUMMA(A1:E1*{1\2\3\4\5})

Matriskonstanter kan innehålla tal, text, logiska värden (till exempel SANT och FALSKT) och felvärden (till exempel #SAKNAS). Du kan använda heltal, decimaltal och tal i exponentialform. Om du använder text måste du omge texten med dubbla citattecken (").

Matriskonstanter kan inte innehålla ytterligare matriser, formler eller funktioner. Med andra ord: de kan endast innehålla text eller tal som separeras av semikolon eller omvänt snedstreck. I Excel visas ett varningsmeddelande när du anger en formel, till exempel {1\2\A1:D4} eller {1\2\SUMMA(Q2:Z8)}. Numeriska värden kan inte innehålla procenttecken, dollartecken, punkter eller parenteser.

Ett av de bästa sätten att använda matriskonstanter är att namnge dem. Namngivna konstanter kan vara mycket enklare att använda och namnet kan dölja lite av komplexiteten med matrisformlerna för andra användare. Så här gör du när du vill namnge en matriskonstant och använda den i en formel:

1. Klicka på Definiera namn i gruppen Definierade namn på fliken Formler.
   Dialogrutan Definiera namn visas.

2. I rutan Namn skriver du Kvartal1.

3. Ange följande konstant i rutan Refererar till (kom ihåg att skriva in klammerparenteserna manuellt):

   ={”Januari”\”Februari”\”Mars”}

   Innehållet i dialogrutan ser nu ut så här:

   

4. Klicka på OK och markera en rad med tre tomma celler.

5. Skriv in följande formel och tryck sedan på Ctrl+Skift+Retur.

   =Kvartal1

   Följande resultat visas.

   

När du använder en namngiven konstant som en matrisformel ska du komma ihåg att ange likhetstecknet. Om du inte gör det tolkas matrisen som en textsträng och formeln fungerar inte som avsett. Kom också ihåg att du kan använda kombinationer av text och tal.

Om matriskonstanterna inte fungerar kan du undersöka om följande problem har uppstått:

• Vissa element kanske inte har avgränsats med rätt tecken. Om du utelämnar ett semikolon eller ett omvänt snedstreck, eller om du placerar ett tecken på fel ställe, kanske matriskonstanten inte skapas korrekt, eller så kan ett varningsmeddelande visas.

• Du kan ha markerat ett cellområde som inte motsvarar antalet element i konstanten. Om du till exempel markerar en kolumn med sex celler som ska användas i en konstant med fem celler, visas felvärdet #SAKNAS i den tomma cellen. Omvänt gäller att om du markerar för få celler utelämnas de värden som saknar en motsvarande cell.

I exemplen nedan visas några sätt som du kan använda matriskonstanter i matrisformler. I vissa exempel används funktionen TRANSPONERA för att konvertera rader till kolumner och tvärtom.

Multiplicera alla element i en matris

1. Skapa ett nytt kalkylblad och markera ett block med tomma celler som är fyra kolumner brett och tre rader högt.

2. Skriv in följande formel och tryck sedan på Ctrl+Skift+Retur:

   ={1\2\3\4;5\6\7\8;9\10\11\12}*2

Upphöja elementen i en matris i kvadrat

1. Markera ett block med tomma celler som är fyra kolumner brett och tre rader högt.

2. Skriv in följande matrisformel och tryck sedan på Ctrl+Skift+Retur:

   ={1\2\3\4;5\6\7\8;9\10\11\12}*{1\2\3\4;5\6\7\8;9\10\11\12}

   Du kan också ange den här matrisformeln som använder operatorn cirkumflex (^):

   ={1\2\3\4;5\6\7\8;9\10\11\12}^2

Transponera en endimensionell rad

1. Markera en kolumn med fem tomma celler.

2. Skriv in följande formel och tryck sedan på Ctrl+Skift+Retur:

   =TRANSPONERA({1\2\3\4\5})

   Även om du angav en vågrät matriskonstant konverteras matriskonstanten till en kolumn med funktionen TRANSPONERA.

Transponera en endimensionell kolumn

1. Markera en rad med fem tomma celler.

2. Skriv in följande formel och tryck sedan på Ctrl+Skift+Retur:

   =TRANSPONERA({1;2;3;4;5})

Även om du angav en lodrät matriskonstant konverteras konstanten till en rad med funktionen TRANSPONERA.

Transponera en tvådimensionell konstant

1. Markera ett block med celler som är tre kolumner brett och fyra rader högt.

2. Ange följande konstant och tryck sedan på Ctrl+Skift+Retur:

   =TRANSPONERA({1\2\3\4;5\6\7\8;9\10\11\12})

   Med funktionen TRANSPONERA konverteras varje rad till en serie kolumner.

Det här avsnittet innehåller exempel på grundläggande matrisformler.

Skapa matriser och matriskonstanter från befintliga värden

I exemplet nedan får du veta hur du använder matrisformler för att skapa länkar mellan cellområden i olika kalkylblad. Du får också se hur du skapar en matriskonstant från samma uppsättning värden.

Skapa en matris från befintliga värden

1. Markera cellerna C8:E10 i ett kalkylblad i Excel och ange den här formeln:

   ={10\20\30;40\50\60;70\80\90}

   Glöm inte att ange { (vänster klammerparentes) innan du anger 10 och } (höger klammerparentes) efter att du anger 90 eftersom du skapar en matris med tal.

2. Tryck påCtrl+Skift+Retur, som anger den här matrisen med tal i cellområdet C8:E10 med hjälp av en matrisformel. I kalkylbladet bör C8 till E10 se ut så här:

   10	20	30
   40	50	60
   70	80	90

3. Markera cellområdet C1 till E3.

4. Ange följande formel i formelfältet och tryck sedan på Ctrl+Skift+Retur:

   =C8:E10

   En 3x3-matris av celler visas i cellerna C1 till E3 med samma värden som visas i C8 till E10.

Skapa en matriskonstant från befintliga värden

1. Växla till redigeringsläge genom att trycka påF2 när cellerna C1:C3 är markerade. 

2. Tryck F9 om du vill konvertera cellreferenserna till värden. Excel konverterar värdena till en matriskonstant. Formeln ska nu vara ={10\20\30;40\50\60;70\80\90}.

3. Tryck på Ctrl+Skift+Retur för att ange matriskonstanten som en matrisformel.

Räkna tecken i ett cellområde

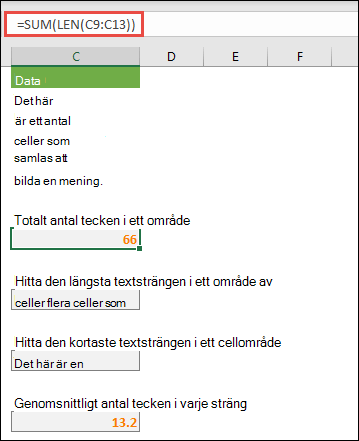
I följande exempel visas hur du räknar antalet tecken, inklusive mellanslag, i ett cellområde.

1. Kopiera den här tabellen och klistra in den i cell A1 i ett kalkylblad.

   Data
   Det här är ett
   antal celler som
   samlas
   för att bilda en
   enda mening.
   Totalt antal tecken i A2:A6
   =SUMMA(LÄNGD(A2:A6))
   Innehåll i längsta cell (A3)
   =INDEX(A2:A6,MATCHA(MAX(LÄNGD(A2:A6)),LÄNGD(A2:A6),0),1)

2. Markera cell A8 och tryck sedan på Ctrl+Skift+Retur för att se det totala antalet tecken i cellerna A2:A6 (66).

3. Markera cell A10 och tryck sedan på Ctrl+Skift+Retur för att se innehållet i den längsta av cellerna A2:A6 (cell A3).

Följande formel används i cell A8 och räknar det sammanlagda antalet tecken (66) i cellerna A2 till A6.

=SUMMA(LÄNGD(A2:A6))

I det här fallet returnerar funktionen LÄNGD längden på varje textsträng i var och en av cellerna i området. Sedan adderas dessa värden med funktionen SUMMA och resultatet (66) visas.

Hitta de n lägsta värdena i ett område

I exemplet visas hur du hittar de tre lägsta värdena i ett cellområde.

1. Ange vissa slumptal i cellerna A1:A11.

2. Markera cellerna C1 till och med C3. Den här uppsättningen celler innehåller de resultat som returneras av matrisformeln.

3. Skriv in följande formel och tryck sedan på Ctrl+Skift+Retur:

   =SMALL(A1:A11,{1;2;3})

Den här formeln använder en matriskonstant för att utvärdera funktionen SMALL tre gånger och returnera det minsta (1), sekunds minsta (2) och tredje minsta (3) medlemmar i matrisen som finns i cellerna A1:A10 Om du vill hitta fler värden lägger du till fler argument till konstanten. Du kan också använda ytterligare funktioner med den här formeln, till exempel SUMMA eller MEDEL. Till exempel:

=SUMMA(LITEN(A1:A10,{1\2\3})

=MEDEL(LITEN(A1:A10,{1\2\3})

Hitta de n högsta värdena i ett område

Om du vill hitta de högsta värdena i ett område kan du ersätta funktionen MINSTA med funktionen STÖRSTA. Dessutom används funktionerna RAD och INDIREKT i exemplet nedan.

1. Markera cellerna D1 till och med D3.

2. Ange den här formeln i formelfältet och tryck sedan på Ctrl+Skift+Returr:

   =LARGE(A1:A10,ROW(INDIRECT("1:3")))

I det här läget kan det vara bra att känna till lite grann om funktionerna RAD och INDIREKT. Du kan använda funktionen RAD när du vill skapa en matris med upprepade heltal. Du kan till exempel markera en tom kolumn med 10 celler i arbetsboken med övningen, ange den här matrisformeln och sedan trycka på Ctrl+Skift+Retur:

=RAD(1:10)

Formeln skapar en kolumn med tio heltal i följd. Om du vill se ett potentiellt problem infogar du en rad ovanför området som innehåller matrisformeln (d.v.s. ovanför rad 1). Radreferenserna justeras i Excel och formeln genererar heltal från 2 till 11. Du kan åtgärda problemet genom att lägga till funktionen INDIREKT i formeln:

=RAD(INDIREKT("1:10"))

I funktionen INDIREKT används textsträngar som argument (vilket är anledningen till att området 1:10 omges av dubbla citattecken). Textvärden justeras inte när du infogar rader eller flyttar matrisformeln på något annat sätt. Resultatet blir att funktionen RAD alltid genererar den matris med heltal som du vill ha.

Vi tar en titt på formeln som du använde tidigare – =STÖRSTA(A5:A14;RAD(INDIREKT("1:3"))) – med början från den inre parentesen och arbetar utåt: Funktionen INDIREKT returnerar en uppsättning textvärden, i det här fallet värdena 1 till 3. Funktionen RAD genererar i sin tur en kolumnmatris med tre celler. Funktionen STOR använder värdena i cellområdet A5:A14 och utvärderas tre gånger, en gång för varje referens som returneras av funktionen RAD. The values 3200, 2700, and 2000 are returned to the three-cell columnar array. If you want to find more values, you add a greater cell range to the INDIRECT function.

Som med tidigare exemplar, använda den här formeln med andra funktioner, till exempel SUMMA och MEDEL.

Hitta den längsta textsträngen i ett cellområde

Gå tillbaka till det tidigare exemplet med textsträngar, ange följande formel i en tom cell och tryck på Ctrl+Skift+Retur:

=INDEX(A2:A6,MATCHA(MAX(LÄNGD(A2:A6)),LÄNGD(A2:A6),0),1)

Texten "flera celler som" visas.

Vi tittar närmare på formeln, med början från inre element och arbetar utåt. Funktionen LÄNGD returnerar längden på varje post i cellområdet A2:A6. Funktionen MAX beräknar det största värdet bland dessa element, som motsvarar den längsta textsträngen, som finns i cell A3.

Det är nu det börjar bli komplicerat. Med funktionen PASSA beräknas adressen (den relativa positionen) för den cell som innehåller den längsta textsträngen. För detta behövs tre argument: ett sökvärde, en sökmatris och en passningstyp. Funktionen PASSA söker efter sökvärdet i sökmatrisen. I det här fallet är sökvärdet den längsta textsträngen:

(MAX(LÄNGD(A2:A6))

och den strängen finns i den här matrisen:

LÄNGD(A2:A6)

Argumentet för passningstypen är 0. Passningstypen kan bestå av värdet 1, 0 eller -1. Om du anger 1 returnerar PASSA det högsta värdet som är lägre än eller lika med sökvärdet. Om du anger 0 returnerar PASSA det första värdet som är exakt lika med sökvärdet. Om du anger -1 returnerar PASSA det lägsta värdet som är högre än eller lika med det angivna sökvärdet. Om du utelämnar passningstypen används 1 som standard.

Slutligen används de här argumenten av funktionen INDEX: en matris samt ett värde som anger rad och kolumn inom den matrisen. Cellområdet A2:A6 står för matrisen, funktionen PASSA står för celladressen och det sista argumentet (1) anger att värdet kommer från den första kolumnen i matrisen.

Det här avsnittet innehåller exempel på avancerade matrisformler.

Summera ett område som innehåller felvärden

Funktionen SUMMA i Excel fungerar inte när du försöker summera ett område som innehåller ett felvärde, till exempel #N/A. I det här exemplet får du veta hur du summerar värdena i ett område med namnet Data som innehåller fel.

=SUMMA(OM(ÄRFEL(Data),"",Data))

Formeln skapar en ny matris som innehåller de ursprungliga värdena minus eventuella felvärden. Om vi börjar från de innersta funktionerna och jobbar oss utåt söker funktionen ÄRFEL efter fel i cellområdet (Data). Funktionen OM returnerar ett visst värde om ett villkor som du anger valideras som SANT och ett annat värde om det valideras till FALSKT. I det här fallet returneras tomma strängar ("") för alla felvärden eftersom de valideras till SANT, och de återstående värdena från området (Data) returneras, eftersom de valideras till FALSKT, vilket innebär att de inte innehåller felvärden. Funktionen SUMMA räknar sedan ut totalsumman för den filtrerade matrisen.

Räkna antalet felvärden i ett område

Det här exemplet påminner om formeln ovan, men den returnerar antalet felvärden i ett område med namnet Data i stället för att filtrera ut dem:

=SUMMA(OM(ÄRFEL(Data),1,0))

Den här formeln skapar en matris som innehåller värdet 1 för de celler som innehåller fel och värdet 0 för celler som inte innehåller fel. Du kan förenkla formeln och få samma resultat genom att ta bort det tredje argumentet till funktionen OM, på det här sättet:

=SUMMA(OM(ÄRFEL(Data),1))

Om du inte anger argumentet returnerar funktionen IF värdet FALSKT om en cell inte innehåller ett felaktigt värde. Du kan förenkla formeln ännu mer:

=SUMMA(OM(ÄRFEL(Data)*1))

Den här varianten fungerar eftersom SANT*1=1 och FALSKT*1=0.

Summera värden baserat på villkor

I vissa situationer kan du behöva summera värden baserat på villkor. I den här matrisformeln summeras till exempel enbart positiva heltal i ett område med namnet Försäljning:

=SUMMA(OM(Försäljning>0,Försäljning))

Funktionen OM skapar en matris med positiva värden och falska värden. Funktionen SUMMA ignorerar praktiskt taget de falska värdena eftersom 0+0=0. Cellområdet som du använder i den här formeln kan bestå av vilket antal rader och kolumner som helst.

Du kan också summera värden som uppfyller fler än ett villkor. I den här matrisformeln beräknas till exempel värden som är högre än 0 och lägre än eller lika med 5:

=SUMMA((Försäljning>0)*(Försäljning<=5)*(Försäljning))

Kom ihåg att den här formeln returnerar ett fel om området innehåller en eller flera celler som inte innehåller tal.

Du kan också skapa matrisformler som använder ett slags ELLER-villkor. Du kan till exempel summera värden som är lägre än 5 och högre än 15:

=SUMMA(OM((Försäljning<5)+(Försäljning>15),Försäljning))

Funktionen OM hittar alla värden som är lägre än 5 och högre än 15 och lämnar sedan vidare dessa värden till funktionen SUMMA.

Det går inte att använda funktionerna OCHoch ELLER direkt i matrisformler eftersom dessa funktioner returnerar ett enda resultat, antingen SANT eller FALSKT, och matrisfunktionerna kräver resultatmatriser. Du kan lösa problemet genom att använda den logik som visas i den föregående formeln. Med andra ord: du utför matematiska operationer, till exempel addition eller multiplikation, på värden som uppfyller villkoret ELLER eller OCH.

Beräkna ett genomsnitt som utesluter nollvärden

I det här exemplet beskrivs hur du tar bort nollvärden från ett område när du behöver räkna ut ett genomsnitt för värdena i det området. I formeln används ett dataområde med namnet Försäljning:

=MEDEL(OM(Försäljning<>0,Försäljning))

Funktionen OM skapa en matris med värden som inte är lika med 0 och lämnar sedan dessa värden vidare till funktionen MEDEL.

Beräkna antalet skillnader mellan två cellområden

I den här matrisformeln jämförs värdena i två cellområden med namnen Minadata och Dinadata och antalet skillnader mellan de två returneras. Om innehållet i de två områdena är identiskt returnerar formeln 0. Om du vill använda den här formeln måste cellområdena ha samma storlek och samma dimension (om Minadata till exempel är ett område med 3 rader och 5 kolumner måste Dinadata också bestå av 3 rader och 5 kolumner):

=SUMMA(OM(Minadata=Dinadata,0,1))

Formeln skapar en ny matris i samma storlek som de områden som du jämför. Funktionen OM fyller i matrisen med värdet 0 och värdet 1 (0 för felaktiga matchningar och 1 för identiska celler). Funktionen SUMMA returnerar summan av värdena i matrisen.

Du kan förenkla formeln så här:

=SUMMA(1*(Minadata<>Dinadata))

Precis som formeln som räknar felvärden i ett område, fungerar den här formeln eftersom SANT*1=1 och FALSKT*1=0.

Hitta platsen för det högsta värdet i ett område

Den här matrisformeln returnerar radnumret för det högsta värdet i ett enkolumnsområde med namnet Data:

=MIN(OM(Data=MAX(Data);RAD(Data);""))

Funktionen OM skapar en ny matris som motsvarar området Data. Om en motsvarande cell innehåller det högsta värdet i området innehåller matrisen radnumret. I annat fall innehåller matrisen en tom sträng (""). Funktionen MIN använder den nya matrisen som sitt andra argument och returnerar det lägsta värdet, som motsvarar radnumret för det högsta värdet i området Data. Om området Data innehåller identiska högsta värden returnerar formeln raden för det första värdet.

Om du vill returnera den faktiska celladressen för ett maxvärde kan du använda den här formeln:

=ADRESS(MIN(OM(Data=MAX(Data);RAD(Data);""));KOLUMN(Data))